Las deformaciones que sufren las vigas debido a las cargas aplicadas deben ser evaluadas y controladas dentro de unos límites de seguridad. Para ello existen diferentes métodos de cálculo y análisis de desplazamientos y giros. En este artículo explicamos en qué consiste y cómo utilizar los teoremas de Mohr. También tenemos un vídeo explicativo y con otros ejemplos resueltos al final del artículo.
Si tenéis dudas sobre algún concepto previo u os estáis iniciando en el cálculo de vigas, os recomendamos ojear este artículo previo.
1. Giros y desplazamientos en vigas
En primer lugar, es necesario establecer qué entendemos por deformaciones en una viga. Una deformación es toda aquella alteración de la geometría de la viga, respecto de su estado inicial, debido a la aplicación de una carga. Las deformación se clasifican en:
- Desplazamientos: se refieren a traslados de posición, verticales u horizontales, de una sección concreta de la viga, con respecto a su posición inicial (antes de la aplicación de la carga). El término flecha suele utilizarse para referirse a desplazamientos verticales (dirección perpendicular al eje de la viga), indicando la distancia entre la fibra neutra de la viga inicial y la fibra neutra de la viga deformada.
- Giros: rotación de una sección de la viga con respecto de la posición inicial (antes de la aplicación de la carga). Se define mediante el ángulo que existe entre la tangente de la directriz de la viga inicial (dirección del eje de la viga) y la directriz de la viga deformada. Si el giro se produce en sentido horario se tomará como negativo, siendo positivo el sentido antihorario.
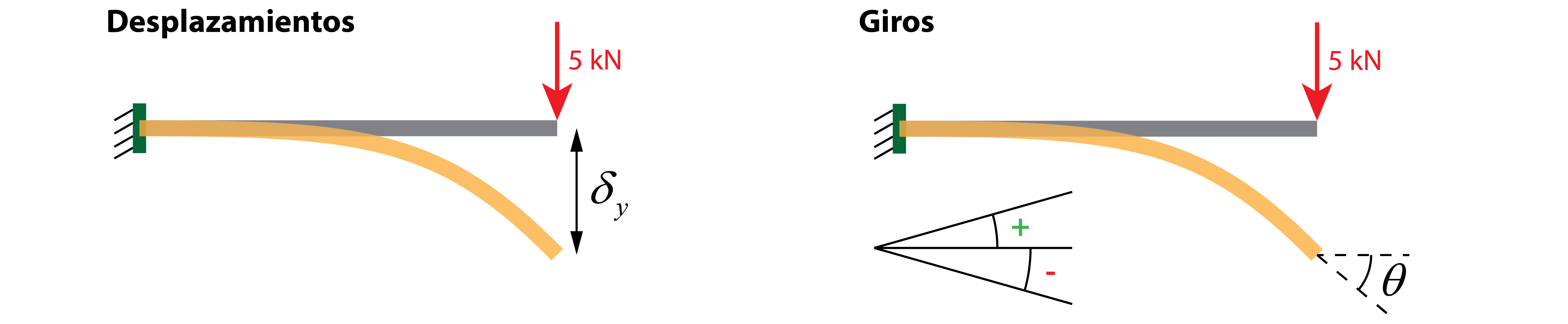
2. Explicación de los teoremas de Mohr
Los teoremas de Mohr representan una herramienta muy útil para el cálculo de desplazamientos y giros en vigas, una vez que se han obtenido las leyes de momento flector. Los teoremas de Mohr permiten obtener deformaciones relativas entre dos secciones de una viga, por lo que pueden utilizarse para calcular deformaciones en secciones concretas. Sin embargo no permiten describir la deformación completa en una viga como sí aporta el método de integración de la elástica. A continuación se describen los dos teoremas:
- Primer teorema de Mohr (cálculo de giros): este primer teorema permite obtener el giro relativo entre dos secciones a y b, {\theta _b} – {\theta _a}, mediante la integración de la ley de momento flector, M, entre ambas secciones. Por lo tanto, si conocemos el giro absoluto de la sección a, {\theta _a}, es posible deducir el giro absoluto de la sección b, {\theta _b}.
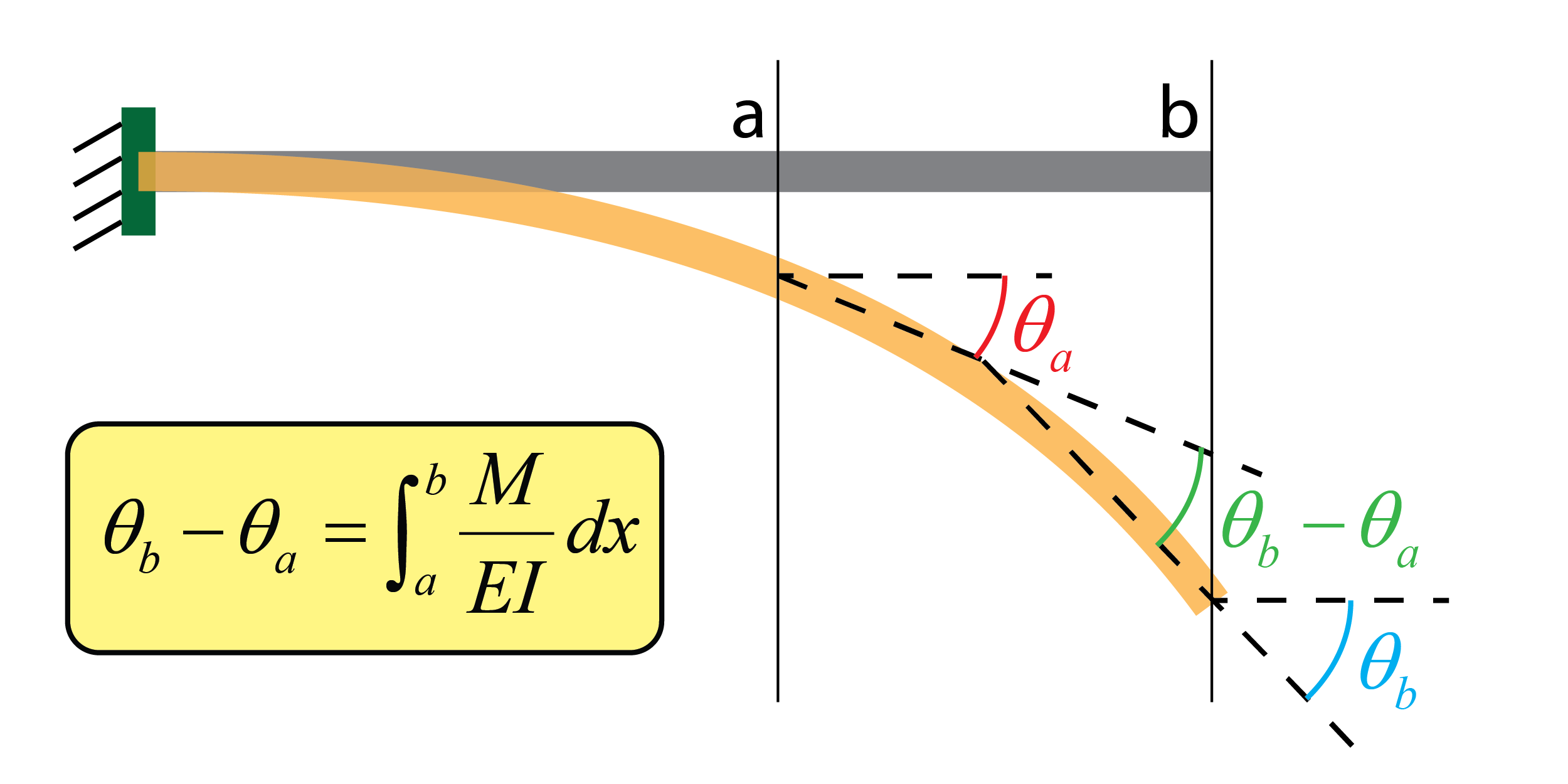
Obtención del giro absoluto en b utilizando el primer teorema de Mohr
{\theta _b} = {\theta _a} + \int_a^b {\dfrac{M}{{EI}}dx}
- Segundo teorema de Mohr (cálculo de desplazamientos): el segundo teorema permite obtener el desplazamiento relativo entre dos secciones a y b, {y_b} – {y_a}. Para ello, tiene en cuenta el giro de la sección a, {\theta _a}, la distancia entre ambas secciones, ({x_b} – {x_a}) y la integración de la ley de momento flector, M. Por lo tanto, si conocemos el giro y la flecha en la sección a, es posible deducir la flecha en la sección b, {y_b}.
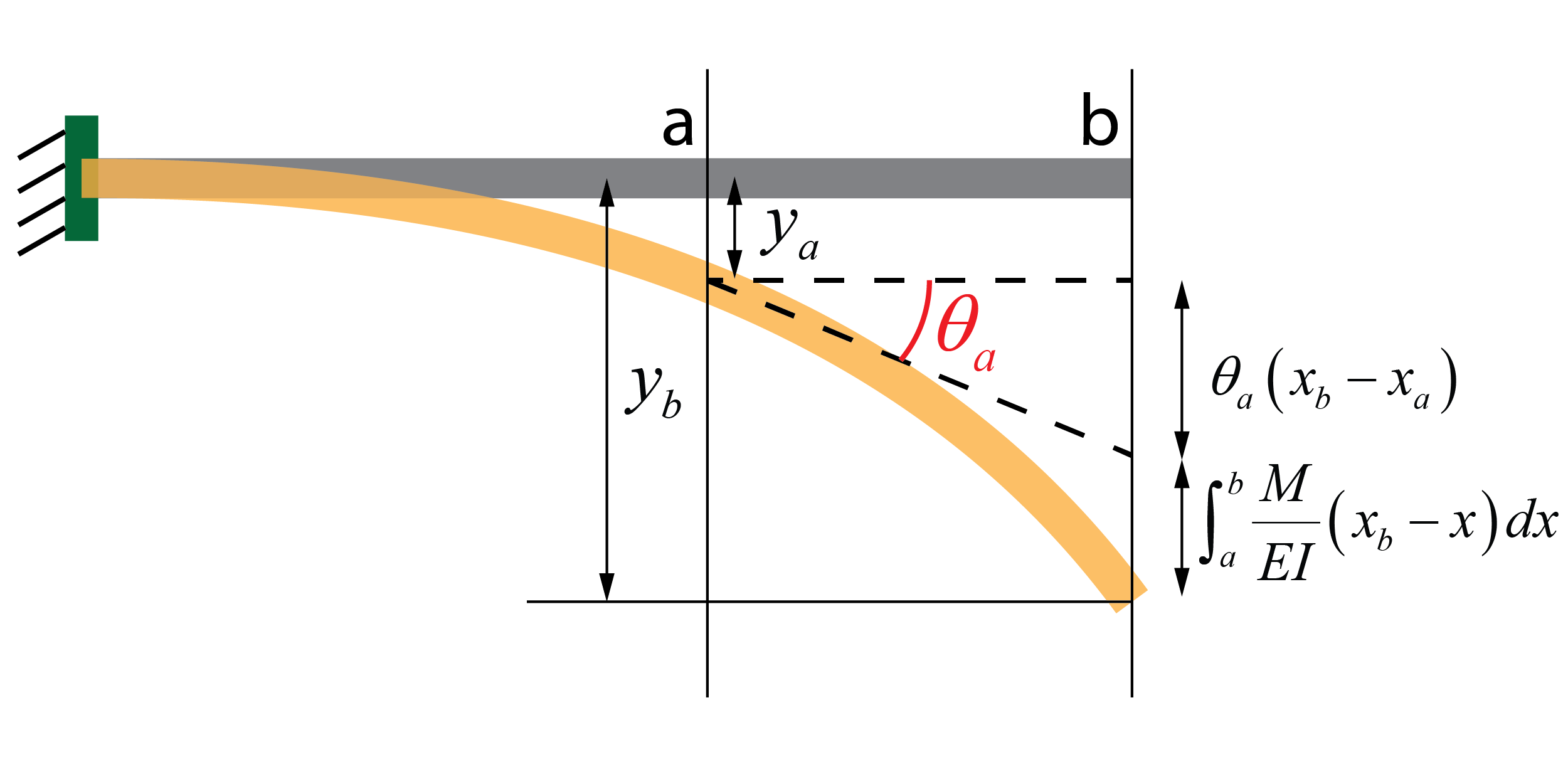
Obtención del desplazamiento absoluto en b utilizando el segundo teorema de Mohr
{y_b} = {y_a} + {\theta _a}\left( {{x_b} – {x_a}} \right) + \int_a^b {\dfrac{M}{{EI}}\left( {{x_b} – x} \right)dx}
3. Aplicación en un ejercicio
Para entender el método, vamos a aplicarlo para resolver un caso sencillo.
Obtener el giro y el desplazamiento vertical en la sección c de esta viga empotrada utilizando los teoremas de Mohr. El material es acero S275 (E = 210000 MPa) y el perfil de la viga es IPE 120 (I = 318 cm^4).

Como la viga del ejercicio es empotrada, utilizar los teoremas de Mohr para obtener el giro y el desplazamiento vertical en la sección c es muy sencillo si tomamos como referencia la sección a, que ni gira ni se desplaza al estar empotrada.
El primer paso necesario para obtener las deformaciones aplicando los teoremas de Mohr es resolver la viga, calculando las reacciones y las leyes de momento flector. Esta viga se encuentra resuelta en un artículo previo sobre la resolución de vigas con cargas triangulares. Podéis revisar cómo se resuelve en el siguiente enlace.
Aquí mostraremos simplemente los resultados para las leyes de momento flector de los dos tramos de la viga.
- Tramo a-b
\begin{array}{c} \left. {M\left( x \right)} \right|_a^b = – Ma + Ray \cdot x – q'x \cdot \dfrac{x}{2} – \dfrac{{\left( {q – q'} \right)x}}{2} \cdot \dfrac{{2x}}{3} = \\\\ = – 15 + 15x – \left( {10 – \dfrac{{10}}{3}x} \right) \cdot x \cdot \dfrac{x}{2} – \left( {10 – 10 + \dfrac{{10}}{3}x} \right) \cdot \dfrac{x}{2} \cdot \dfrac{{2x}}{3} = \\\\ = – 15 + 15x – 5{x^2} + \dfrac{5}{9}{x^3}\;kNm \\ \end{array}
- Tramo b-c
\left. {M\left( x \right)} \right|_b^c = – Ma + Ray \cdot x – \dfrac{{q \cdot 3}}{2} \cdot \left( {x – 1} \right) = – 15 + 15x – \dfrac{{10 \cdot 3}}{2} \cdot \left( {x – 1} \right) = 0\;kNm
Únicamente hay momento flector en el tramo a-b, siguiendo una distribución polinómica de grado 3. En el tramo b-c el momento flector es nulo al ser un voladizo sin cargas aplicadas.
Cálculo del giro en la sección c
Para obtener el giro en la sección c haremos uso del primer teorema de Mohr, tomando como referencia la sección a.
{\theta _c} = {\theta _a} + \int_a^c {\dfrac{M}{{EI}}dx}
Como a es un empotramiento, sabemos que {\theta _a} = 0\;rad. Sustituyendo el resto de términos de la fórmula obtenemos
{\theta _c} = {\theta _a} + \int_a^c {\dfrac{M}{{EI}}dx} = 0 + \dfrac{1}{{EI}}\int_0^3 {\left( { – 15 + 15x – 5{x^2} + \dfrac{5}{9}{x^3}} \right)dx} =
= \dfrac{1}{{EI}}\left[ { – 15x + \dfrac{{15{x^2}}}{2} – \dfrac{{5{x^3}}}{3} + \dfrac{{5{x^4}}}{{36}}} \right]_0^3 = \dfrac{{ – 11,25}}{{EI}} = \dfrac{{ – 11,25 \cdot {{10}^9}}}{{210000 \cdot 318 \cdot {{10}^4}}} = – 0,017\;rad
Por lo tanto, la sección c gira -0,017 rad. El signo negativo indica que el giro se produce en sentido horario, tal y como se muestra en el criterio de signos visto anteriormente.
NOTA: es importante entender las potencias en base 10 que aparecen multiplicando a los términos al final del cálculo. La fórmula da como resultado un giro en radianes, que es adimensional, por lo que debemos trabajar con las unidades necesarias para que todas se cancelen. En el denominador tenemos el módulo elástico, E, en MPa, es decir N/mm², y la inercia del perfil, I. Como está en cm^4, se multiplica por 10^4 para pasarla a mm^4. El número del numerador representa la multiplicación de M\cdot dx, cuyas unidades respectivas son kNm y m. Para pasar a N y mm aparece la multiplicación por 10^{9}. Así, todos los términos están expresados en N y mm, dando como resultado una longitud en mm.
Cálculo del desplazamiento en la sección c
De igual manera que para el cálculo del giro, tomamos como referencia la sección a por ser un empotramiento. En este caso utilizaremos el segundo teorema de Mohr.
{y_c} = {y_a} + {\theta _a}\left( {{x_c} – {x_a}} \right) + \int_a^c {\dfrac{M}{{EI}}\left( {{x_c} – x} \right)dx}
Sustituyendo los términos de la ecuación, con {\theta _a} = 0\;rad y {y_a} = 0\;mm, resulta
{y_c} = {y_a} + {\theta _a}\left( {{x_c} – {x_a}} \right) + \int_a^c {\dfrac{M}{{EI}}\left( {{x_c} – x} \right)dx} =
= 0 + 0 \cdot \left( {5 – 0} \right) + \dfrac{1}{{EI}}\int_0^3 {\left( { – 15 + 15x – 5{x^2} + \dfrac{5}{9}{x^3}} \right) \cdot \left( {5 – x} \right)dx} =
= \dfrac{1}{{EI}}\int_0^3 {\left( { – 75 + 90x – 40{x^2} + \dfrac{{70}}{9}{x^3} – \dfrac{5}{9}{x^4}} \right)dx} =
= \dfrac{{ – 44,5}}{{EI}} = \dfrac{{ – 44,5 \cdot {{10}^{12}}}}{{210000 \cdot 318 \cdot {{10}^4}}} = – 74,12\;mm
Por lo tanto, la sección c se desplaza 74,12 mm. El signo negativo del desplazamiento indica que se produce en sentido vertical y hacia abajo, de acuerdo con el criterio de signos.
NOTA: es importante entender las potencias en base 10 que aparecen multiplicando a los términos al final del cálculo. La fórmula da como resultado un desplazamiento en unidades de longitud (metros, centímetros, milímetros…), por lo que debemos trabajar con las unidades necesarias para que resulte una lontitud. En el denominador tenemos el módulo elástico, E, en MPa, es decir N/mm², y la inercia del perfil, I. Como está en cm^4, se multiplica por 10^4 para pasarla a mm^4. El número del numerador representa la multiplicación de M\cdot (x_c – x) \cdot dx, cuyas unidades respectivas son kNm, m y m. Para pasar a N y mm aparece la multiplicación por 10^{12}. Así, todos los términos están expresados en N y mm, dando como resultado una longitud en mm.
Por último, no te pierdas el siguiente vídeo con animaciones donde también resolvemos otros ejemplos.
