Las deformaciones que sufren las vigas debido a las cargas aplicadas deben ser evaluadas y controladas dentro de unos límites de seguridad. Para ello existen diferentes métodos de cálculo y análisis de desplazamientos y giros. En este artículo explicamos en qué consiste y cómo utilizar los Teorema de Castigliano. También tenemos un vídeo explicativo y con otros ejemplos resueltos al final del artículo.
Si tenéis dudas sobre algún concepto previo u os estáis iniciando en el cálculo de vigas, os recomendamos ojear este artículo previo.
1. Giros y desplazamientos en vigas
En primer lugar, es necesario establecer qué entendemos por deformaciones en una viga. Una deformación es toda aquella alteración de la geometría de la viga, respecto de su estado inicial, debido a la aplicación de una carga. Las deformación se clasifican en:
- Desplazamientos: se refieren a traslados de posición, verticales u horizontales, de una sección concreta de la viga, con respecto a su posición inicial (antes de la aplicación de la carga). El término flecha suele utilizarse para referirse a desplazamientos verticales (dirección perpendicular al eje de la viga), indicando la distancia entre la fibra neutra de la viga inicial y la fibra neutra de la viga deformada.
- Giros: rotación de una sección de la viga con respecto de la posición inicial (antes de la aplicación de la carga). Se define mediante el ángulo que existe entre la tangente de la directriz de la viga inicial (dirección del eje de la viga) y la directriz de la viga deformada. Si el giro se produce en sentido horario se tomará como negativo, siendo positivo el sentido antihorario.
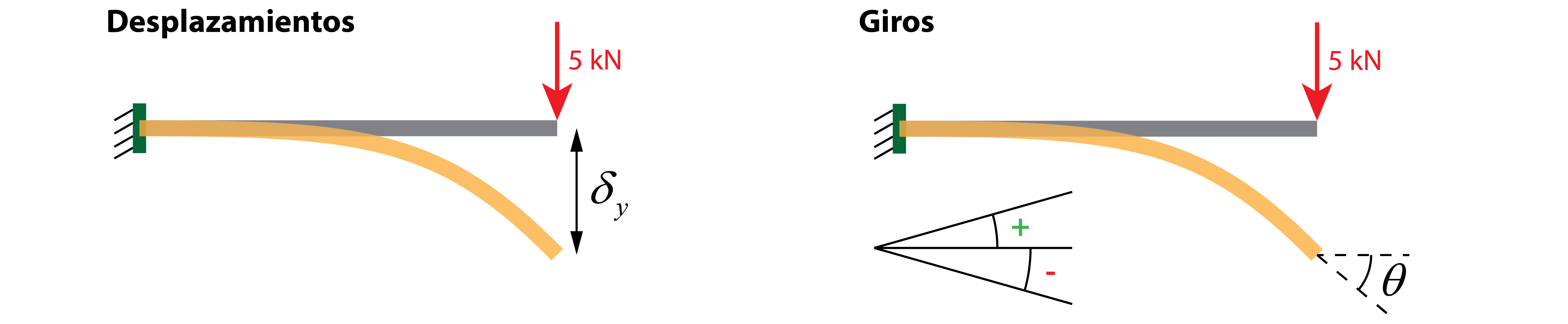
2. Explicación del segundo teorema de Castigliano
Castigliano fue un ingeniero italiano del siglo XIX que desarrolló avances muy importantes en el ámbito del cálculo estructural y los medios continuos. Postuló dos teoremas, siendo el segundo de ellos el que se puede emplear para obtener giros y desplazamientos en secciones específicas de una viga.
Enunciado del segundo teorema de Castigliano: la derivada parcial de la energía elástica de un sólido respecto de cada una de las cargas aplicadas sobre él es igual a la deformación en el punto de aplicación de la carga según la dirección de la misma.
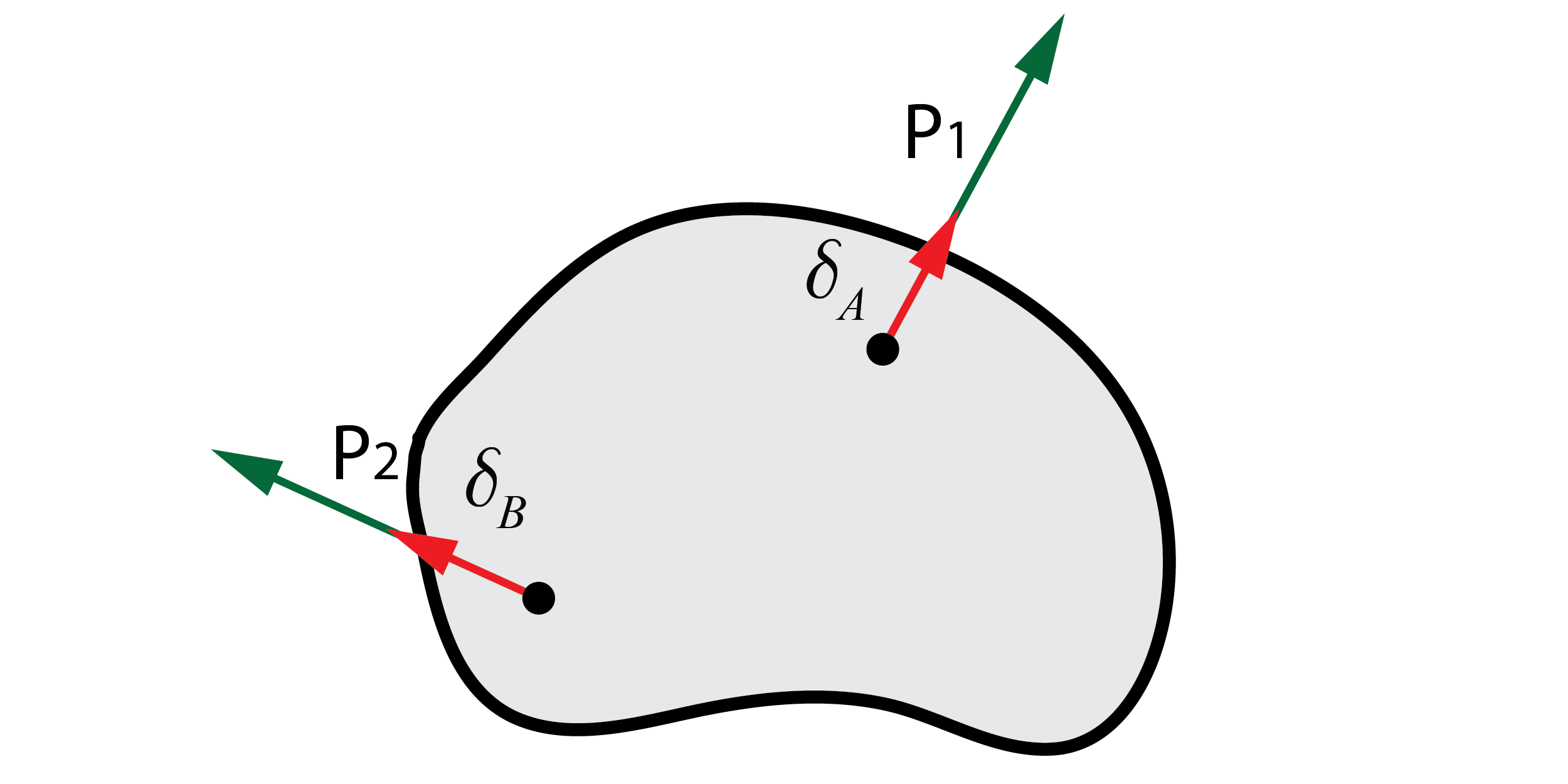
Formulación matemática del segundo teorema de Castigliano
{\delta _i} = \dfrac{{\partial U}}{{\partial {P_i}}}
Este teorema postula que, si la expresión de la energía elástica del sólido, U, es conocida, cualquier deformación, ya sea giro o desplazamiento, en un punto concreto del sólido puede calcularse derivando con respecto de la carga, P, que haya aplicada en dicho punto. El resultado indicará la deformación siguiendo el sentido de aplicación de la carga P.
En el caso del dibujo anterior, si la energía elástica se deriva con respecto de la carga P_1, se obtendrá la deformación \delta_A.
La energía elástica, U, es la energía interna de deformación producida en el sólido por las cargas aplicadas sobre él. En una viga, la energía elástica depende de los distintos esfuerzos a los que está sometida a lo largo de toda su longitud, según la ecuación
U = \int_0^L {\dfrac{{{N^2}}}{{2EA}}dx} + \int_0^L {\dfrac{{M_z^2}}{{2E{I_z}}}dx} + \int_0^L {\dfrac{{M_y^2}}{{2E{I_y}}}dx}
donde N es el esfuerzo axil, M_z y M_y son los momentos flectores según los dos ejes del perfil, E es el módulo elástico del material, A el área del perfil, I_z e I_y son los momentos de inercia del perfil con respecto a cada eje.
Como se puede comprobar en la fórmula, el esfuerzo cortante y el esfuerzo de torsión no son tenidos en cuenta debido a su baja aportación con respecto al resto de esfuerzos.
Además, normalmente el esfuerzo de flexión suele ser el esfuerzo predominante en vigas, pudiendo despreciar también la contribución del esfuerzo axial, reescribiendo la fórmula como
U = \int_0^L {\dfrac{{M_z^2}}{{2E{I_z}}}dx} + \int_0^L {\dfrac{{M_y^2}}{{2E{I_y}}}dx}
En función de las cargas que haya en la viga puede existir momento flector en ambos ejes o únicamente en uno de ellos, lo que simplifica el cálculo.
En el caso de estructuras articuladas, únicamente existirá esfuerzo axial, reescribiendo la fórmula como
U = \int_0^L {\dfrac{{{N^2}}}{{2EA}}dx}
Siguiendo el teorema, la deformación, \delta_i, calculada como la derivada de la energía elástica con respecto a una carga, P_i aplicada en una sección de la viga es
{\delta _i} = \int_0^L {\dfrac{N}{{EA}}\dfrac{{\partial N}}{{\partial {P_i}}}dx} + \int_0^L {\dfrac{{{M_z}}}{{E{I_z}}}\dfrac{{\partial {M_z}}}{{\partial {P_i}}}dx} + \int_0^L {\dfrac{{{M_y}}}{{E{I_y}}}\dfrac{{\partial {M_y}}}{{\partial {P_i}}}dx}
Es decir, para obtener la deformación es necesario conocer la expresión de las leyes de esfuerzos (normalmente solo se necesitará conocer la ley de momento flector al considerar el resto de esfuerzos como despreciables), la derivada de estas leyes con respecto de la carga P_i considerada, y las propiedades del material y perfil de la viga.
Se obtendrá un desplazamiento o un giro en función de si la carga respecto a la que se deriva es una carga puntual o un momento. Si el resultado es positivo, el sentido de la deformación es el mismo que el sentido de la carga o el momento, siendo contrario si el resultado es negativo.
¿Para qué es útil el teorema? Este teorema permite calcular giros y desplazamientos en posiciones concretas de una viga, es decir, en una sección si conocemos a priori las leyes de esfuerzos. No es posible obtener la deformación en toda la viga, como sí aporta el método de integración de la curva elástica. La principal ventaja del método es que es sencillo de utilizar, ya que las derivadas no suelen ser complejas al tratarse de funciones polinómicas, pudiendo ser un procedimiento sustituto al método de la carga unidad. También puede utilizarse en cualquier tipo de viga, lo que favorece su uso con respecto a los métodos de Mohr.
3. Aplicación en un ejercicio
Para entender el método, vamos a aplicarlo para resolver un caso sencillo.
Obtener el desplazamiento vertical en la sección b de esta viga biapoyada utilizando el teorema de Castigliano. El material es acero S275 (E = 210000 MPa) y el perfil de la viga es IPE 120 (I = 318 cm^4).

Como el desplazamiento que se quiere calcular en la sección b coincide con el punto de aplicación de la carga P, podemos aplicar el teorema de Castigliano para obtenerlo de manera sencilla.
Para obtener el desplazamiento vertical en la sección b de esta viga por el método de Castigliano es necesario obtener la ley de momento flector en todos los tramos de la viga, para poder derivarla con respecto a la carga P.
En primer lugar, obtendremos las reacciones en los apoyos en función de la carga P, utilizando las tres ecuaciones del balance estático global de la viga (sumatorio de fuerzas verticales y horizontales y equilibrio de momentos).
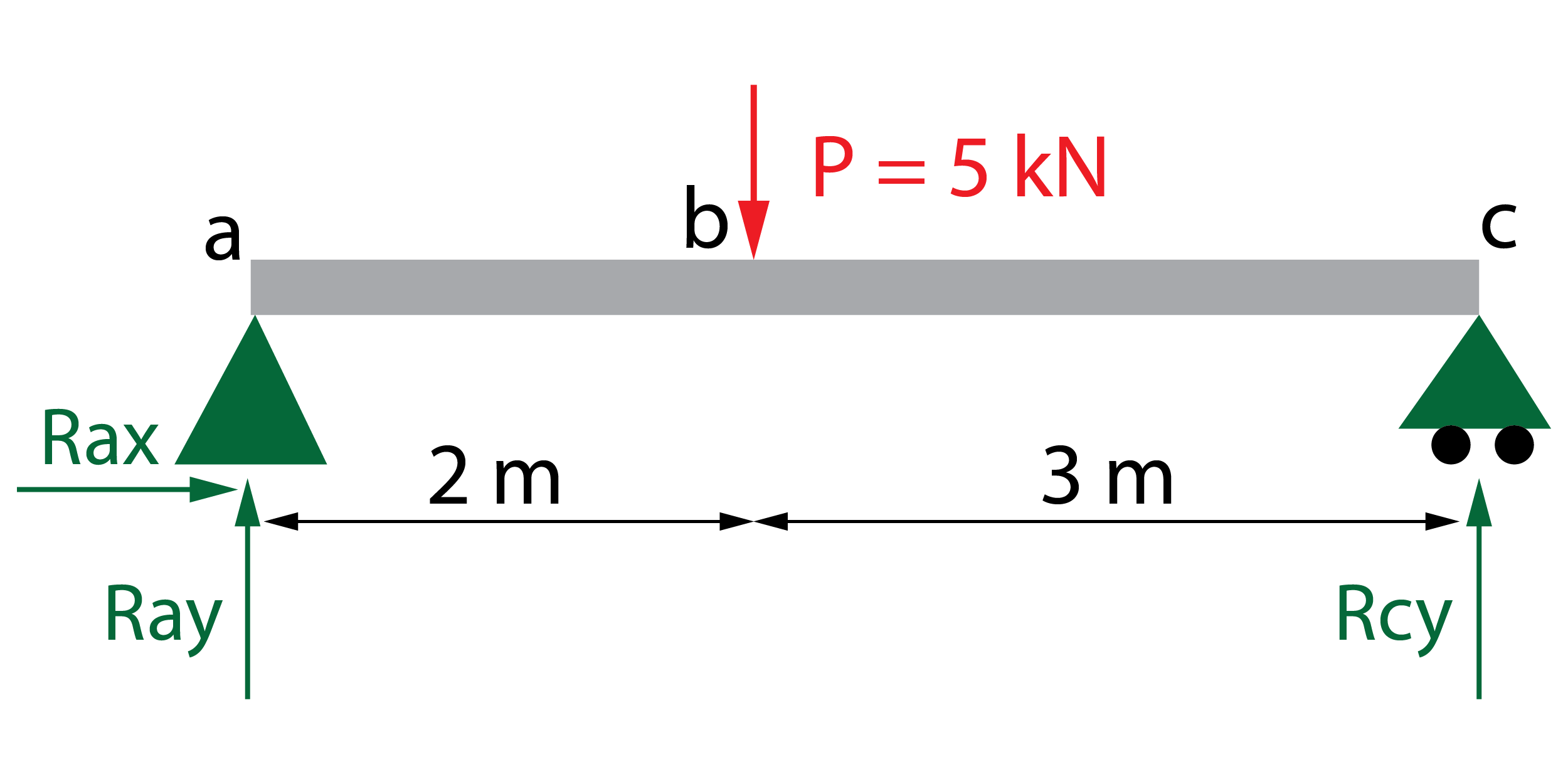
Balance estático
\sum {{F_x} = 0 \to Rax = 0}
\sum {{F_y} = 0} \to Ray + Rcy – P = 0
\sum {M = 0} \to – 2P + 5Rcy = 0
A partir de la tercera ecuación se obtiene Rcy = \dfrac{{2P}}{5}\;kN y sustituyendo en la segunda ecuación se calcula Ray = \dfrac{{3P}}{5}\;kN.
El siguiente paso es calcular la ley de momento flector en los dos tramos, a-b y b-c, de la viga, en función de la carga P.
Antes de analizar cada tramo y obtener las leyes de esfuerzo, es necesario definir un criterio de signos.
- Momento flector, M: se tomará como criterio de momento positivo, el sentido horario producido por las cargas situadas a la izquierda de la sección x.
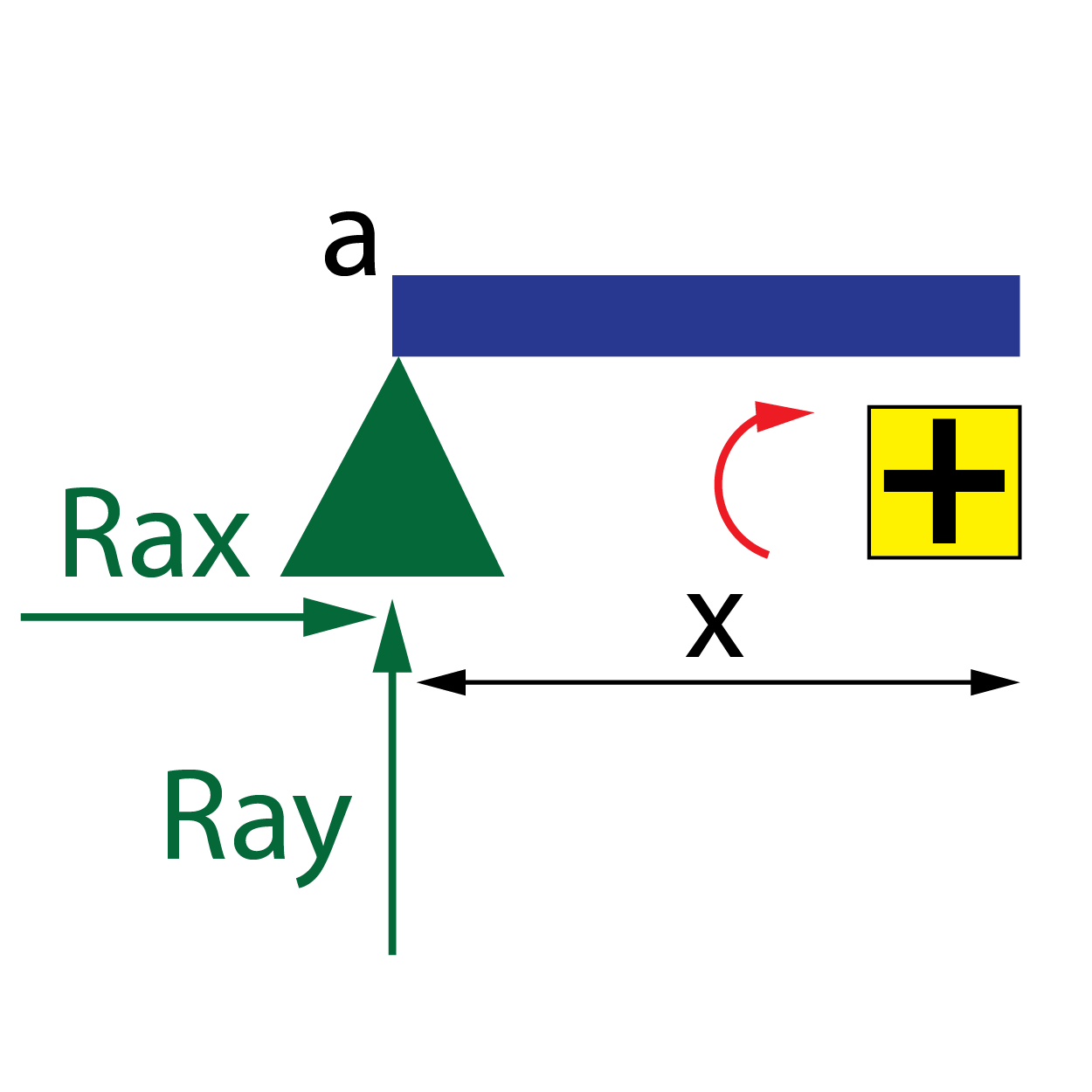
A partir de estos criterios establecidos, podemos obtener las leyes de esfuerzos en cada uno de los tramos.
Tramo a-b
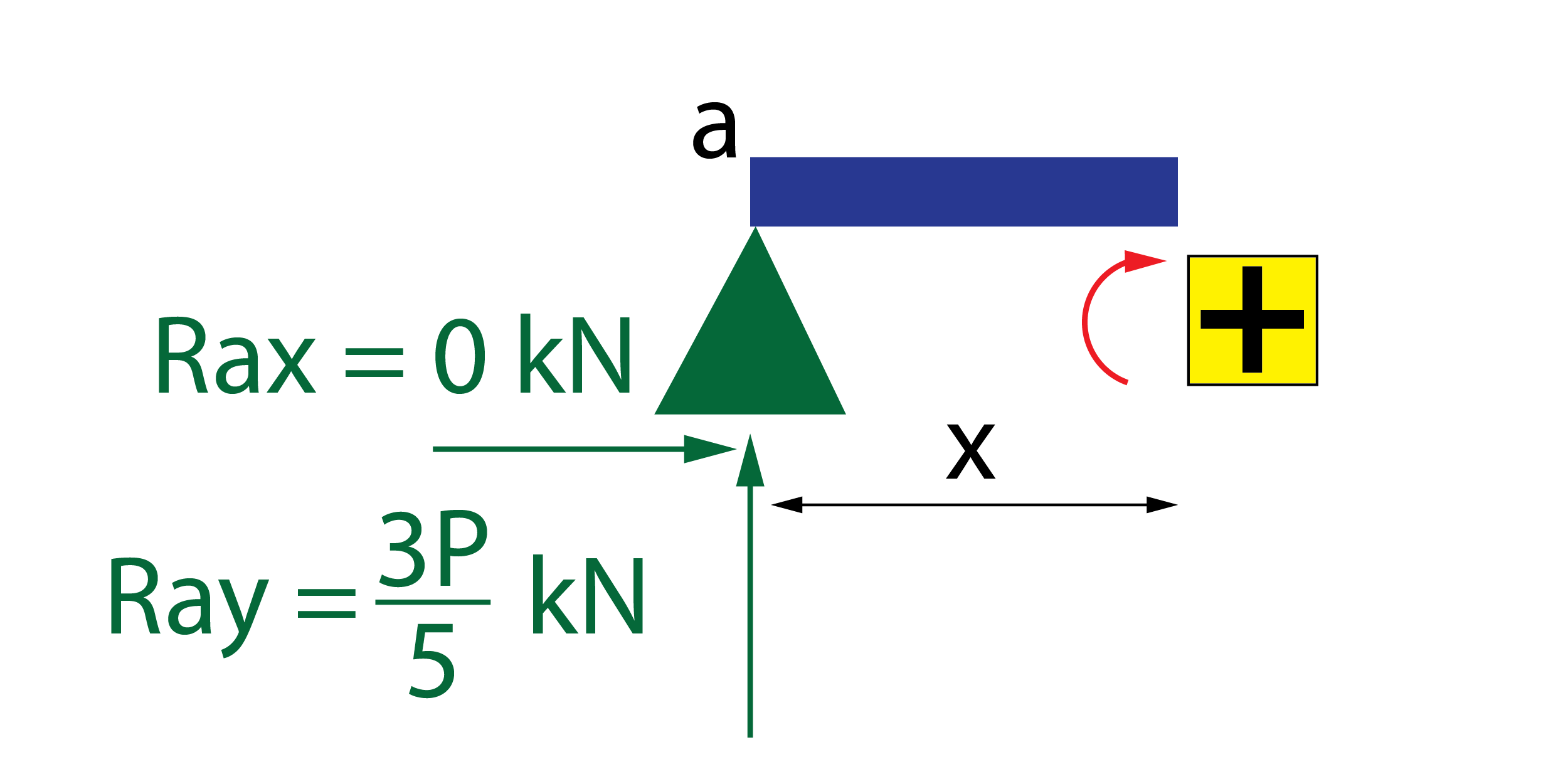
El momento flector es generado por la reacción Ray, cuya distancia a la sección x es la distancia x. Genera un momento en sentido positivo.
\left. {M(x)} \right|_a^b = \dfrac{{3P}}{5}x\;kNm
A partir de esta expresión del momento flector como función de la carga P, se calcula la derivada como
\dfrac{{\partial \left. {M(x)} \right|_a^b}}{{\partial P}} = \dfrac{3}{5}x\;m
Aquí hay que observar como la derivada del momento flector respecto de la carga P tiene unidades de longitud (metros).
Como el valor de la carga P es conocido (5 kN), sustituyendo su valor obtenemos la ley de momento flector que será necesaria en la fórmula del teorema de Castigliano como
\left. {M(x)} \right|_a^b = 3x\;kNm
Tramo b-c
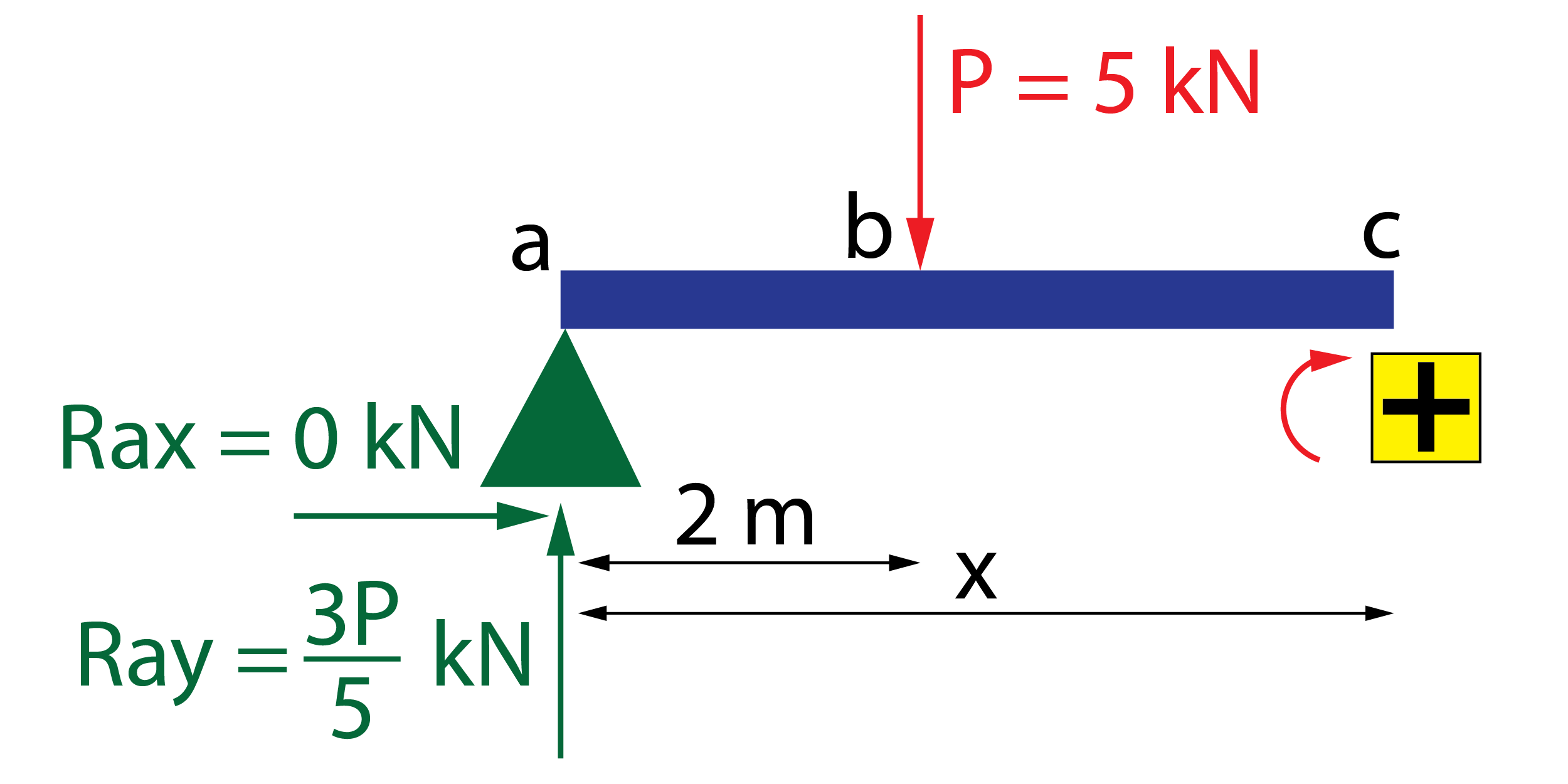
El momento flector es generado por la reacción Ray, cuya distancia a la sección x es la distancia x. Genera un momento en sentido positivo. Además, la carga P genera un momento negativo, multiplicada por la distancia (x-2).
\left. {M(x)} \right|_b^c = \dfrac{{3P}}{5}x – P \cdot \left( {x – 2} \right) = – \dfrac{{2P}}{5}x + 2P\;kNm
A partir de esta expresión del momento flector como función de la carga P, se calcula la derivada como
\dfrac{{\partial \left. {M(x)} \right|_b^c}}{{\partial P}} = – \dfrac{2}{5}x + 2\;m
Como el valor de la carga P es conocido (5 kN), sustituyendo su valor obtenemos la ley de momento flector que será necesaria en la fórmula del teorema de Castigliano como
\left. {M(x)} \right|_b^c = – 2x + 10\;kNm
Una vez que conocemos las expresiones de la ley de momentos en ambos tramos y la derivada con respecto de la carga P, podemos aplicar el teorema de Castigliano para obtener el desplazamiento vertical en la sección b de la viga.
\delta _y^b = \int_0^L {\dfrac{M}{{EI}}\dfrac{{\partial M}}{{\partial P}}dx} = \dfrac{1}{{EI}}\left[ {\int_0^2 {3x \cdot \dfrac{3}{5}x\;dx} + \int_2^5 {\left( { – 2x + 10} \right) \cdot } \left( {\dfrac{2}{5}x + 2} \right)dx} \right] =
= \dfrac{1}{{EI}}\left[ {\int_0^2 {\dfrac{{9{x^2}}}{5}dx} + \int_2^5 {\left( {\dfrac{{4{x^2}}}{5} – 8x + 20} \right)dx} } \right] = \dfrac{1}{{EI}}\left( {\left[ {\dfrac{{3{x^3}}}{5}} \right]_0^2 + \left[ {\dfrac{{4{x^3}}}{{15}} – 4{x^2} + 20x} \right]_2^5} \right) =
= \dfrac{1}{{EI}}\left( {\dfrac{{24}}{5} + \dfrac{{36}}{5}} \right) = \dfrac{{12 \cdot {{10}^{12}}}}{{210000 \cdot 318 \cdot {{10}^4}}} = 17,97\;mm
Como el resultado es positivo, el desplazamiento sigue la dirección de la carga aplicada P, siendo un desplazamiento vertical hacia abajo de 17, 97 mm.
NOTA: es importante entender las potencias en base 10 que aparecen multiplicando a los términos al final del cálculo. La fórmula da como resultado un desplazamiento en unidades de longitud (metros, centímetros, milímetros…), por lo que debemos trabajar con las unidades necesarias para que resulte una longitud. En el denominador tenemos el módulo elástico, E, en MPa, es decir N/mm², y la inercia del perfil, I. Como está en cm^4, se multiplica por 10^4 para pasarla a mm^4. El número del numerador representa la multiplicación de la ley de momento flector, por su derivada con respecto de P y por dx, cuyas unidades respectivas son kNm, m y m. Para pasar a N y mm aparece la multiplicación por 10^{12}. Así, todos los términos están expresados en N y mm, dando como resultado una longitud en mm.
4. Truco para obtener desplazamientos en otras secciones
El método de Castigliano también puede utilizarse para obtener desplazamientos en posiciones donde no haya ninguna carga aplicada. Para ello, hay que utilizar una carga ficticia en la sección de análisis y derivar con respecto a ella. En el ejemplo de la siguiente imagen, se utiliza una carga ficticia T (no tiene valor) para obtener el desplazamiento vertical en la sección d.
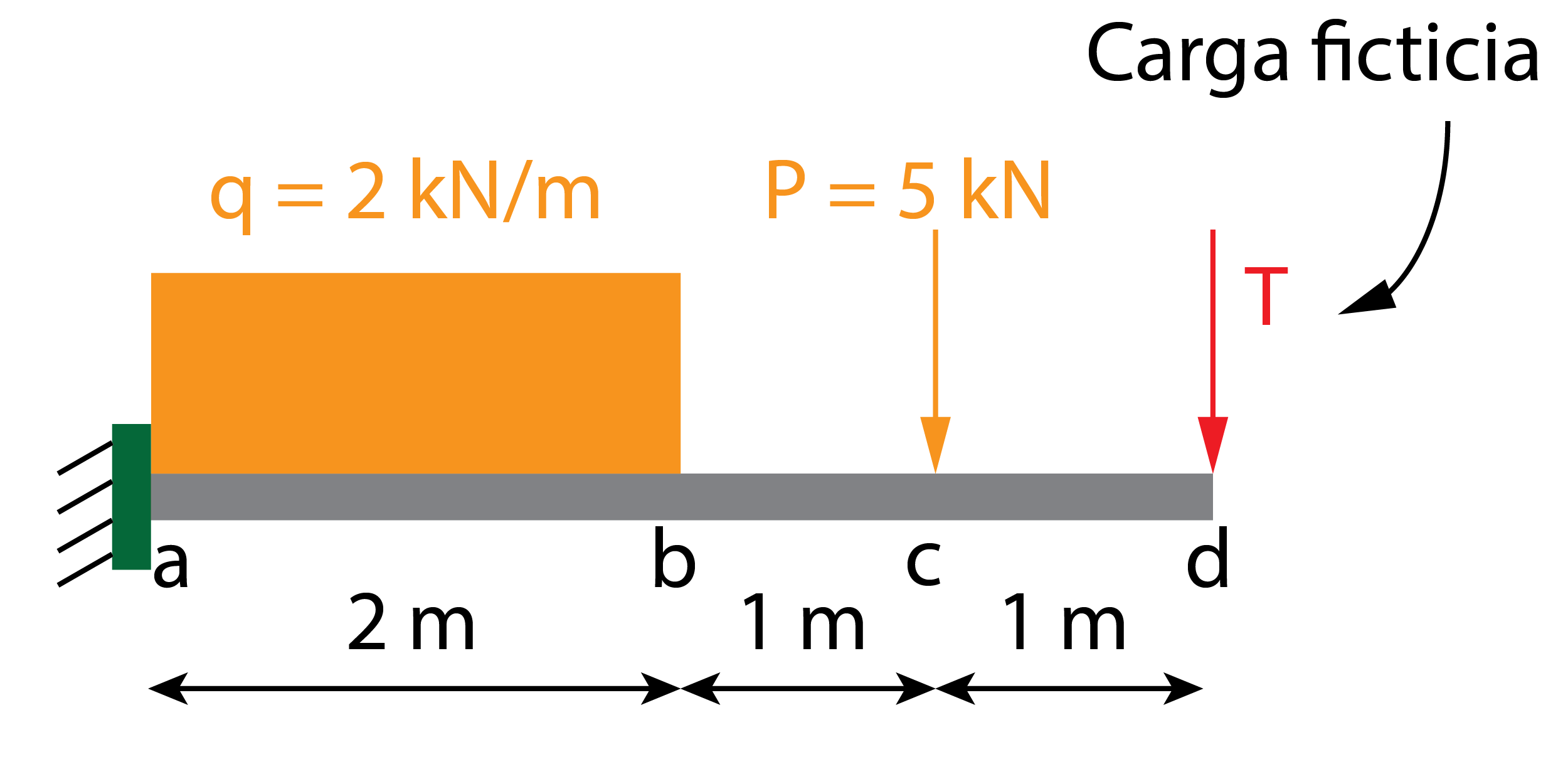
Si quieres aprender cómo se realiza este trucazo con el método de Castigliano no te pierdas el vídeo!!!
