Las deformaciones que sufren las vigas debido a las cargas aplicadas deben ser evaluadas y controladas dentro de unos límites de seguridad. Para ello existen diferentes métodos de cálculo y análisis de desplazamientos y giros. En este artículo explicamos en qué consiste y cómo utilizar el método de integración de la ecuación elástica. También tenemos un vídeo explicativo y con otros ejemplos resueltos al final del artículo.
Si tenéis dudas sobre algún concepto previo u os estáis iniciando en el cálculo de vigas, os recomendamos ojear este artículo previo.
1. Giros y desplazamientos en vigas
En primer lugar, es necesario establecer qué entendemos por deformaciones en una viga. Una deformación es toda aquella alteración de la geometría de la viga, respecto de su estado inicial, debido a la aplicación de una carga. Las deformación se clasifican en:
- Desplazamientos: se refieren a traslados de posición, verticales u horizontales, de una sección concreta de la viga, con respecto a su posición inicial (antes de la aplicación de la carga). El término flecha suele utilizarse para referirse a desplazamientos verticales (dirección perpendicular al eje de la viga), indicando la distancia entre la fibra neutra de la viga inicial y la fibra neutra de la viga deformada.
- Giros: rotación de una sección de la viga con respecto de la posición inicial (antes de la aplicación de la carga). Se define mediante el ángulo que existe entre la tangente de la directriz de la viga inicial (dirección del eje de la viga) y la directriz de la viga deformada. Si el giro se produce en sentido horario se tomará como negativo, siendo positivo el sentido antihorario.
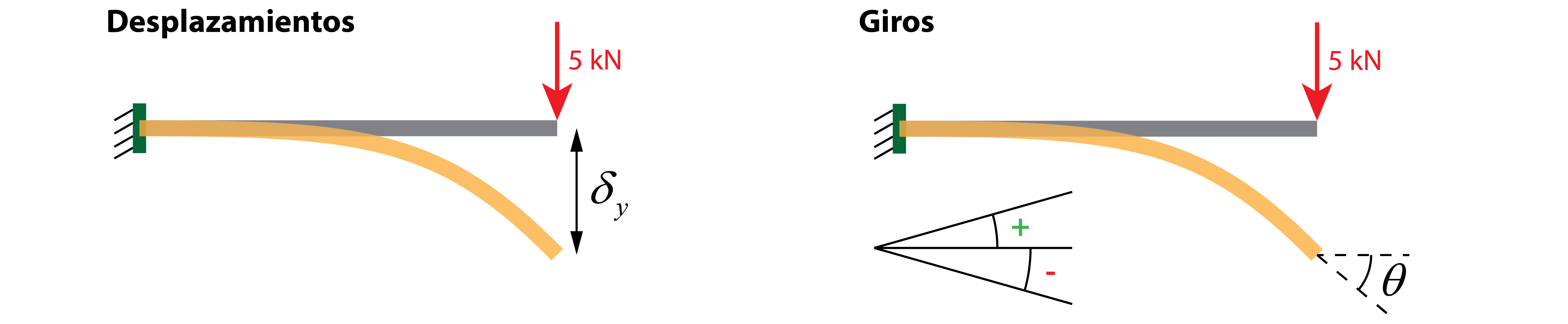
2. Explicación del método de integración de la ecuación elástica
El método de integración de la curva elástica (también llamado método de doble integración) es un procedimiento muy útil para obtener deformaciones en distintos puntos de una viga, ya que permite obtener una descripción completa de la viga deformada. Esto representa la mayor ventaja del método en comparación con otros como los teoremas de Mohr, el método de la carga ficticia o el teorema de Castigliano, que únicamente son útiles si se desea calcular la deformación en una sección concreta de la viga.
Mediante el método de la curva elástica se obtienen dos ecuaciones que representan los giros y los desplazamientos en todas las secciones transversales de la viga, en función de la posición respecto del extremo inicial.
Sin embargo, es un método más laborioso (por lo general) que los procedimientos mencionados anteriormete, ya que es necesario integrar dos veces la ley o leyes de momentos flectores de una viga y calcular una serie de constantes que aparecen como resultado de la integración.
Formulación matemática de la Ecuación de la Elástica
y'' = \dfrac{{{d^2}y}}{{d{x^2}}} = \dfrac{{M\left( x \right)}}{{EI}}
La Ecuación de la Elástica es una ecuación diferencial para una viga de eje recto. Relaciona la flecha o desplazamiento vertical, y, en una sección, con la posición, x, de la sección, a partir de la ley de momento flector, M(x), el módulo elástico del material de la viga, E, y el momento de inercia de la sección, I.
Integrando la ecuación diferencial respecto de la variable x una vez, se obtiene una expresión que representa el giro, \theta \left( x \right) en todas las secciones de la viga. Esta expresión será una función de x, que llamaremos f'(x), más una constante C1, en principio desconocida.
\theta \left( x \right) = \dfrac{{dy}}{{dx}} = \int {\dfrac{{M\left( x \right)}}{{EI}}dx} = f'\left( x \right) + {C_1}
Si esta expresión vuelve a integrarse con respecto de x, se obtiene una representación de la deformación perpendicular a la viga, y(x), para todas las posiciones, x, de la viga. El resultado es una función, f(x), más la constante C1 anterior, multiplicada por x, más una nueva constante de integración C2.
y\left( x \right) = \int {\left( {\int {\frac{{M\left( x \right)}}{{EI}}dx} } \right)dx} = f\left( x \right) + {C_1} \cdot x + {C_2}
Como conclusión, si conocemos la ley de momento flector de la viga, es posible integrarla dos veces, teniendo dos expresiones que describen los giros y desplazamientos verticales en todos los puntos. Las constantes de integración, C1 y C2, se calculan a partir de las condiciones específicas de la viga, y aparecerán distintas constantes para cada tramo de la viga. Los apoyos y restricciones definen el giro y desplazamiento de secciones concretas que servirán para deducir estos valores.
Para entender mejor todo esto, veamos un ejemplo.
3. Aplicación en un ejercicio
Para entender el método, vamos a aplicarlo para resolver un caso sencillo.
Obtener las ecuaciones que describen la deformación de la viga mediante el método de integración de la elástica . El material es acero S275 (E = 210000 MPa) y el perfil de la viga es IPE 120 (I = 318 cm^4).

Se trata de una viga isostática, con una poyo fijo en a y una deslizadera horizontal en b. Aparecerán 3 reacciones en los apoyos, Rax, Ray, Rby, respectivamente. Como se trata de una viga muy fácil de resolver y el objetivo de este artículo es aprender el método de integración de la elástica, no explicaremos los cálculos para realizar el balance estático y obtener los diagramas de momentos flectores.
Partiremos directamente de la ecuación de la ley de momentos para los dos tramos, a-b y b-c de la viga. Podéis comprobar, si queréis, estos resultados.
Tramo a-b
\left. {M\left( x \right)} \right|_a^b = – 5x\;kNm
Tramo b-c
\left. {M\left( x \right)} \right|_b^c = 5x – 20\;kNm
Tramo a-b
En primer lugar comenzamos integrando la ley para el tramo a-b. Como se trata del primer tramo, nombraremos con el subíndice 1 a las expresiones de giros y desplazamientos.
{\theta _1}\left( x \right) = \dfrac{1}{{EI}}\int { – 5x} \,dx = \dfrac{1}{{EI}}\left[ {\dfrac{{ – 5{x^2}}}{2} + {C_1}} \right]
Al obtener la expresión del giro, aparece la constante C1. Seguidamente, volvemos a integrar la expresión anterior para obtener la deformación en la viga.
{y_1}\left( x \right) = \dfrac{1}{{EI}}\int {\left( {\dfrac{{ – 5{x^2}}}{2} + {C_1}} \right)dx} = \dfrac{1}{{EI}}\left[ {\dfrac{{ – 5{x^3}}}{6} + {C_1} \cdot x + {C_2}} \right]
Tramo b-c
Repetimos el proceso anterior utilizando la expresión del tramo b-c. En este caso, nombraremos con el subíndice 2 al tratarse del segundo tramo
{\theta _2}\left( x \right) = \frac{1}{{EI}}\int {\left( {5x – 20} \right)} \,dx = \frac{1}{{EI}}\left[ {\frac{{5{x^2}}}{2} – 20x + {C_3}} \right]
Para no caer en confusiones con las constantes del tramo anterior, nombramos como C3 a la primera constante de integración de este tramo.
{y_2}\left( x \right) = \frac{1}{{EI}}\int {\left( {\frac{{5{x^2}}}{2} – 20x + {C_3}} \right)dx} = \frac{1}{{EI}}\left[ {\frac{{5{x^3}}}{6} – 10{x^2} + {C_3} \cdot x + {C_4}} \right]
Determinación de las constantes a partir de las condiciones de contorno
Aunque ya se han obtenido la expresión de los giros y los desplazamientos en la viga para ambos tramos, es necesario determinar las 4 constantes, C1, C2, C3 y C4, para obtener valores numéricos y finalizar el ejercicio. Para ello, haremos uso de las condiciones de contorno de la viga, es decir, de sus restricciones.
- La viga tiene un apoyo fijo en el apoyo a (x=0), lo que implica que el desplazamiento vertical en esta posición debe ser cero. A partir de esta restricción se deduce fácilmente el valor de C2.
{y_1}\left( 0 \right) = 0 \to 0 = \dfrac{1}{{EI}}\left[ {\dfrac{{ – 5 \cdot {0^3}}}{6} + {C_1} \cdot 0 + {C_2}} \right] \to {C_2} = 0
- El desplazamiento vertical en el apoyo b (x=2) también está restringido por el apoyo deslizante. A partir de la ecuación de los desplazamientos verticales en el primer tramo, obtenemos C1.
{y_1}\left( 2 \right) = 0 \to 0 = \frac{1}{{EI}}\left[ {\dfrac{{ – 5 \cdot {2^3}}}{6} + {C_1} \cdot 2 + 0} \right] \to {C_1} = \dfrac{{10}}{3}
- La ecuación de la deformación en la viga es una ecuación continua. Es decir, el giro en la sección b (x=2), debe ser el mismo, independientemente de si se obtiene a partir de la expresión del tramo 1 o del tramo 2. Esto permite igualar ambas expresiones y despejar C3.
{\theta _1}\left( 2 \right) = {\theta _2}\left( 2 \right) \to \dfrac{1}{{EI}}\left[ {\frac{{ – 5 \cdot {2^2}}}{2} + \dfrac{{10}}{3}} \right] = \dfrac{1}{{EI}}\left[ {\dfrac{{5 \cdot {2^2}}}{2} – 20 \cdot 2 + {C_3}} \right] \to {C_3} = \dfrac{{70}}{3}
- Igualmente, el desplazamiento vertical en el apoyo b (x=2) puede obtenerse a partir de la expresión del segundo tramo. Esto permite calcular C4.
{y_2}\left( 2 \right) = 0 \to 0 = \dfrac{1}{{EI}}\left[ {\dfrac{{5 \cdot {2^3}}}{6} – 10 \cdot {2^2} + \dfrac{{70}}{3} \cdot 2 + {C_4}} \right] \to {C_4} = – \dfrac{{40}}{3}
Ecuaciones finales para el cálculo de giros y desplazamientos verticales en la viga
Finalmente, la ecuación que representa los giros en todas las secciones de la viga se escribe como
{\theta _1}\left( x \right) = \dfrac{1}{{EI}}\left[ {\dfrac{{ – 5{x^2}}}{2} + \dfrac{{10}}{3}} \right]\\\\{\theta _2}\left( x \right) = \dfrac{1}{{EI}}\left[ {\dfrac{{5{x^2}}}{2} – 20x + \dfrac{{70}}{3}} \right]
La ecuación que representa los desplazamientos verticales en cada sección se escribe como
