Una aleación es una mezcla de dos o más elementos químicos, donde al menos uno de ellos es un metal. El ejemplo más famoso quizás sea el acero, una aleación de hierro y carbono, aunque estamos rodeados de muchos tipos de aleaciones distintas con una gran variedad de características y aplicaciones.
Las características de las aleaciones vienen determinadas por la microestructura que forman los elementos al estar combinados, lo que depende de la composición de la aleación. Es decir, varía según la cantidad relativa de los elementos. Para analizar y comprender cómo influye la composición de la aleación, se utilizan los diagramas de equilibrio o diagramas de fases. En este artículo explicamos qué son los diagramas de equilibro de aleaciones con solubilidad parcial en estado sólido. Si tenéis interés en conocer las bases de los diagramas de equilibrio, y el ejemplo más sencillo de aleaciones con solubilidad total en estado sólido, podéis echar un ojo a este artículo previo.
También tenéis un vídeo con animaciones al final del artículo.
1. ¿Qué son las aleaciones con solubilidad parcial en estado sólido?
Para entender los diagramas de fases de este tipo de aleaciones, primero es necesario comprender la diferencia entre aleaciones con solubilidad parcial en estado sólido y las aleaciones con solubilidad total.
Cuando los dos componentes, A y B, de la aleación son solubles para cualquier composición en estado sólido, forman una única fase sólida, por ejemplo \alpha. Es decir, después de solidificar, tras cruzar la línea de solidus, únicamente existirá esta fase, independientemente de la composición de la aleación. Se trata de aleaciones con solubilidad total en estado sólido.
Sin embargo, el caso más común es que, dependiendo de la composición y la temperatura, los componentes de la aleación presenten distinta solubilidad, dando lugar a distintas zonas por debajo de la línea de solidus. Existirán dos fases sólidas distintas, \alpha y \beta, por ejemplo.
- \alpha corresponde con una solución sólida del componente B disuelto en A, lo cuál ocurre para composiciones con porcentajes bajos de B.
- \beta es una solución sólida del componente A disuelto en B, que ocurre para composiciones con bajas cantidades de A.
Toda la zona intermedia del diagrama corresponde con la zona bifásica, donde aparecen ambas fases formando un tipo de microestructura característica llamada eutética, que veremos en profundidad más adelante.
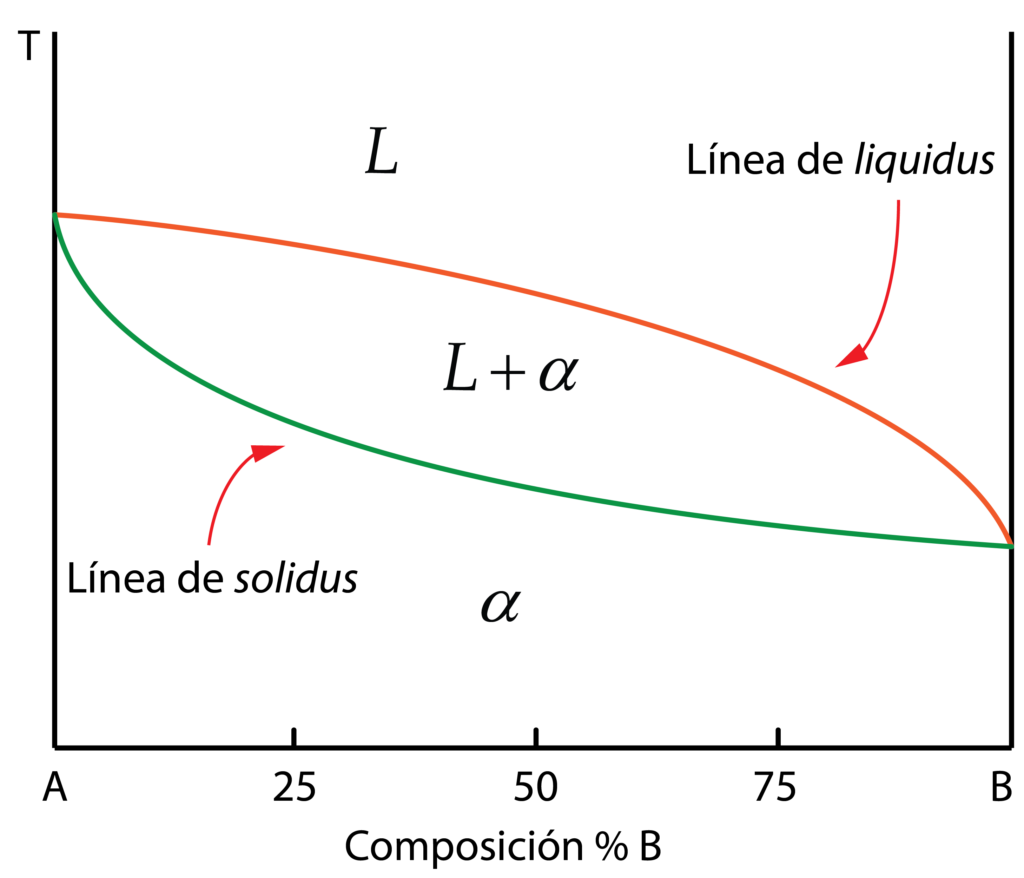
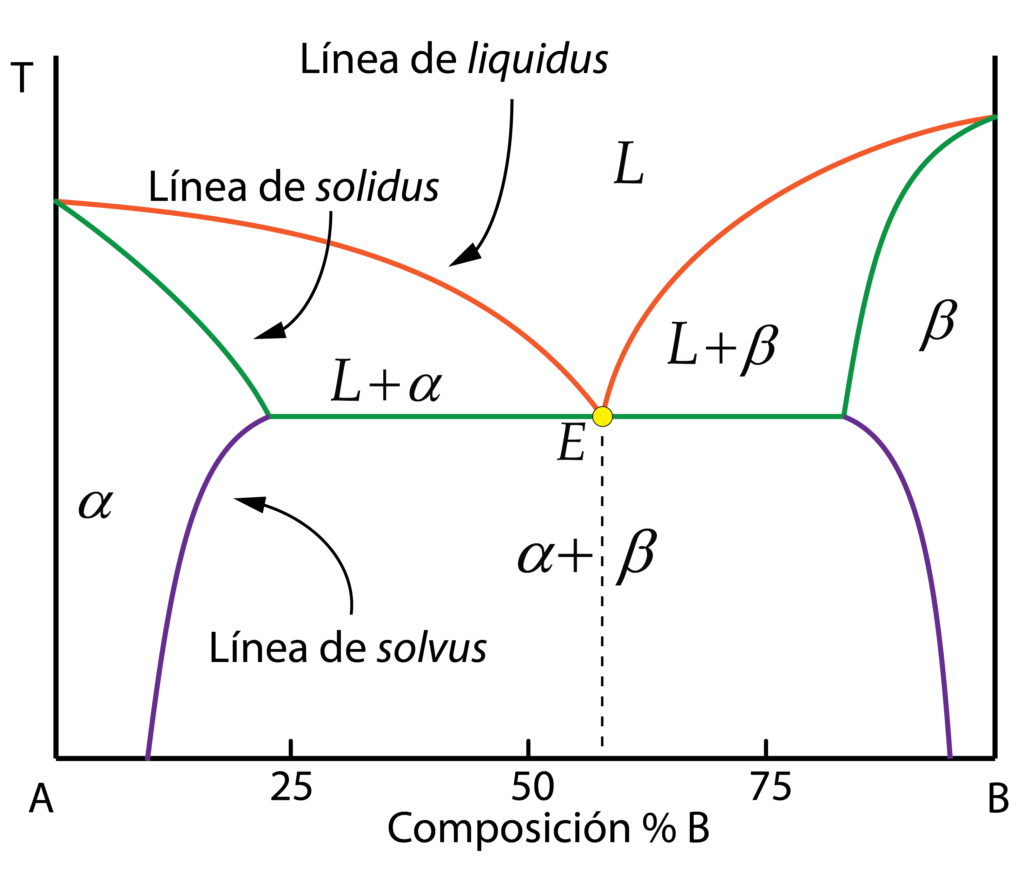
Los diagramas de solubilidad parcial en estado sólido muestran una línea característica adicional a las ya conocidas línea de líquidus y línea de sólidos, llamada línea de solvus. La línea de solvus indica el límite de solubilidad de un componente en otro formado la fase sólida (de B e A formando \alpha o de A en B formando \beta) en función de la temperatura.
Observando la línea de solvus izquierda (la relativa a la fase sólida \alpha) se comprueba cómo, según se reduce la temperatura, la línea de solvus se aproxima al componente A. Esto indica que la solubilidad de B en A para altas temperaturas es mayor (se puede disolver más cantidad), y que se reduce al enfriar al ambiente. De manera análoga ocurre con la solubilidad de A en B. Este detalle tendrá sus efectos en las microestructuras generadas y es muy importante en algunos tipos de aleaciones, como las de aluminio, posibilitando la aplicación de tratamientos térmicos de envejecimiento.
2. ¿Cómo se forma el diagrama?
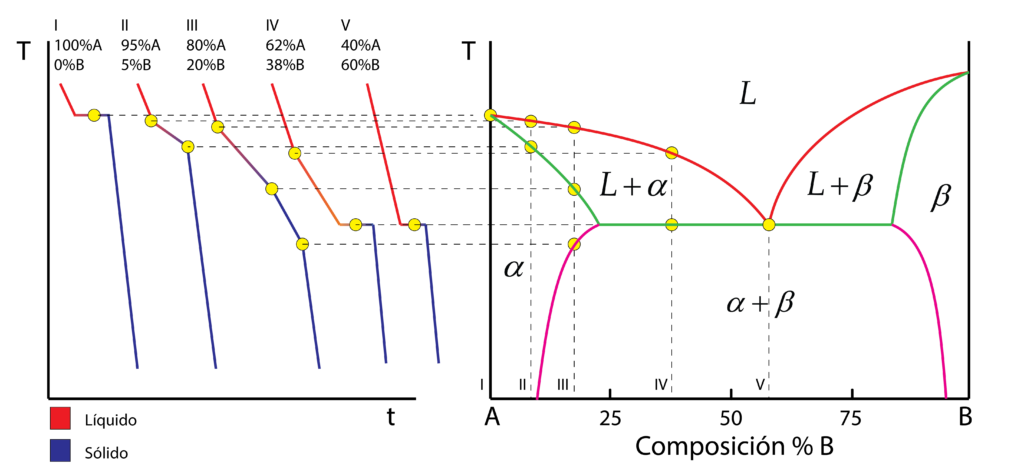
El diagrama se forma a partir de las curvas de enfriamiento de las distintas composiciones de la aleación, dando como resultado cada una de las zonas del diagrama. Pongamos como ejemplo las siguientes 5 composiciones:
- La composición I corresponde con el metal puro A, cuya curva de enfriamiento muestra la zona de solidificación a temperatura constante.
- La composición II es una aleación con el 95% de A y el 5% de B, cuyo proceso de solidificación se lleva a cabo en un rango de temperaturas. Esto se debe a que un componente (aquel con mayor punto de fusión) solidifica antes, mientras el otro todavía se está enfriando.
- La composición III corresponde con una aleación con el 80% de A y el 20% de B, en cuya curva se detectan más zonas. La solidificación se produce, al igual que para III, en un rango de temperaturas, pero mostrando dos zonas en la curva de distinta pendiente.
- La composición IV, del 62% de A y 38% de B, muestra también las 4 zonas. Inicialmente se inicia la solidificación del componente A en un rango de temperaturas, seguida de la solidificación de ambos componentes, a una temperatura constante como si se tratase de un metal puro.
- La composición V corresponde con la composición eutéctica, cuyo proceso de solidificación se lleva a cabo a temperatura constante, como si se tratase de un metal puro.
Podríamos seguir dando más ejemplos de composiciones, viendo ya curvas de enfriamiento semejantes a algunas de las cinco mostradas. Trasladando los puntos de inicio y final de solidificación de cada curva de enfriamiento a un diagrama de equilibrio, donde el eje x representa la composición, y el eje vertical es la temperatura, se obtiene el diagrama de fases. (Nota: el diagrama se forma con la curvas de todas las composiciones, aquí mostradas solo cuatro).
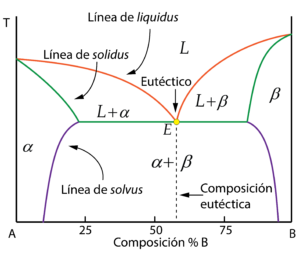
Las partes características del diagrama son:
- Línea de liquidus, por encima de la cual se encuentra la fase líquida.
- Línea de solidus, por debajo de la cual toda la aleación es sólida
- Línea de solvus, que marca los límites de solubilidad en estado sólido, separando las zonas monofásicas de la zona bifásica.
- Punto eutéctico (E), quizás el más característico de estas aleaciones. Se observa para la composición eutéctica, aquella con el menor punto de fusión, donde el líquido solidifica simultáneamente en \alpha + \beta.
- Transformación eutéctica, que es la parte horizontal correspondiente a la línea de solidus. Al cruzarla, el líquido solidifica en \alpha+\beta, formando la microestructura eutéctica.
3. Microestructuras resultantes
Al contrario de lo que ocurre para las aleaciones que presentan un diagrama de solubilidad total, donde en estado sólido únicamente aparece una microestructura monofásica de la fase sólida \alpha, el diagrama de solubilidad parcial conduce a distintos casos, siendo un diagrama de fases mucho más rico.
Para explicar cada uno de ellos, se seleccionan 4 composiciones distintas:
Composición con estructura monofásica
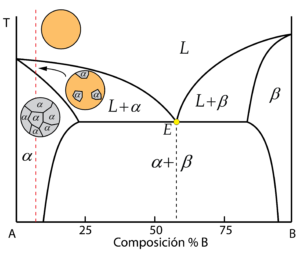
La aleación tiene una composición con un porcentaje de B inferior a la línea de solvus, la cual nunca corta. Analizando la curva de enfriamiento de esta aleación, inicialmente el metal es líquido, comenzando su solidificación en granos de la fase \alpha al cruzar la línea de liquidus (zona bifásica L+\alpha).
Al cruzar la línea de solidus, todo el líquido habrá solidificado formando una única fase sólida \alpha, dando como resultado una microestructura monofásica similar a la vista para aleaciones con solubilidad total en estado sólido.
Nota: un caso similar a este se produce en el otro extremo del diagrama (aleación con un porcentaje alto de B y bajo de A), si la composición de la aleación se sitúa por encima de la línea de solvus de \beta.
Composición con estructura de granos de una fase sólida con precipitados de otra fase
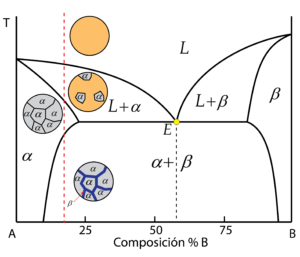
La segunda composición analizada corta la línea de solvus durante el enfriamiento, lo que genera una variación respecto del caso anterior. Inicialmente, comienza a solidificar la fase sólida \alpha, hasta completar la solidificación al cruzar la línea de solidus, obteniendo la microestructura monofásica. Sin embargo, al descender la temperatura, se cruza la línea de solvus, entrando en la zona bifásica \alpha+\beta del diagrama.
Como se ha comentado, la línea de solvus marca la máxima solubilidad de \alpha, la cual se reduce con la temperatura. Esto indica que al cruzar la línea de solvus, la solución sólida \alpha se sobresatura del componente B. Hay mayor cantidad de B disuelto de la que se admite, por lo que este es expulsado por los límites de grano, formándose la solución sólida \beta.
El resultado es una microestructura de granos de \alpha, con \beta precipitado o segregado en los límites de grano.
Nota: de manera simétrica, en la zona derecha del diagrama se obtiene una microestructura de granos de \beta, con \alpha segregado en los límites de grano, si la composición de la aleación es tal que corte a la línea de solvus.
Composición eutéctica
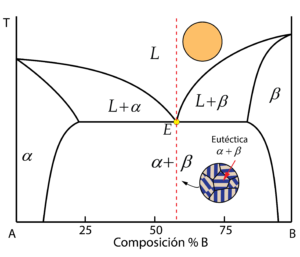
La aleación con la composición eutéctica es aquella que presenta el menor punto de fusión de todo el diagrama, reconocible por el vértice en la línea de liquidus. Encontramos el punto eutéctico, donde se produce la peculiaridad de que coexisten en equilibrio las tres fases: líquido, \alpha y \beta durante el proceso de solidificación. Es decir, directamente se produce la solidificación simultánea de la fase líquida en las fases \alpha y \beta.
La forma en la que ambas fases se distribuyen es muy característica, recibiendo el nombre de microestructura eutéctica, reconocible por mostrar forma de láminas alternas de \alpha y \beta.
El resultado es una microestructura con granos formados por láminas alternas de \alpha y \beta, la microestructura eutética.
Composición hipoeutéctica e hipereutéctica
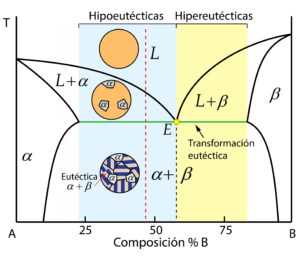
A partir de la composición eutéctica, se clasifican dos nuevos tipos de aleaciones según tengan un contenido en B mayor o menor que la eutéctica.
Las aleaciones hipoeutécticas son aquellas con una composición en B inferior que la eutéctica que cruzan la transformación eutéctica (parte horizontal a temperatura constante de la línea de solidus). Inicialmente, el líquido comenzará a solidificar en la fase \alpha al descender la temperatura (zona bifásica L+\alpha). Conforme la temperatura desciende, la fase líquida disminuye, aumentando la concentración del componente B, hasta alcanzar la transformación eutéctica. A esta temperatura coexisten la solución sólida \alpha y una fase líquida cuya composición es la composición eutéctica. Por lo tanto, al cruzar la transformación eutéctica, la fase líquida solidificará tal cual lo haría una aleación de composición eutéctica, formando \alpha y \beta en láminas alternas.
El resultado es una microesctructura consistente en una matriz eutéctica (\alpha+\beta) con granos dispersos de \alpha proeutéctica, por haberse formado previamente a la transformación eutéctica.
Las aleaciones con una composición en B mayores a la composición eutéctica que cruzan la transformación eutéctica son conocidas como aleaciones hipereutécticas. La microestructura resultante sigue un mecanismo similar al explicado para las aleaciones hipoeutécticas, con la diferencia de que se forma el microconstituyente \beta proeutéctico.
El resultado es una microestructura de matriz eutéctica y con granos dispersos de \beta proeutéctico.
4. Identificación de porcentajes y Regla de la Palanca
La utilidad del diagrama de equilibrio no es únicamente cualitativa, si no que también sirve para cuantificar porcentajes de los componentes y fases de la aleación.
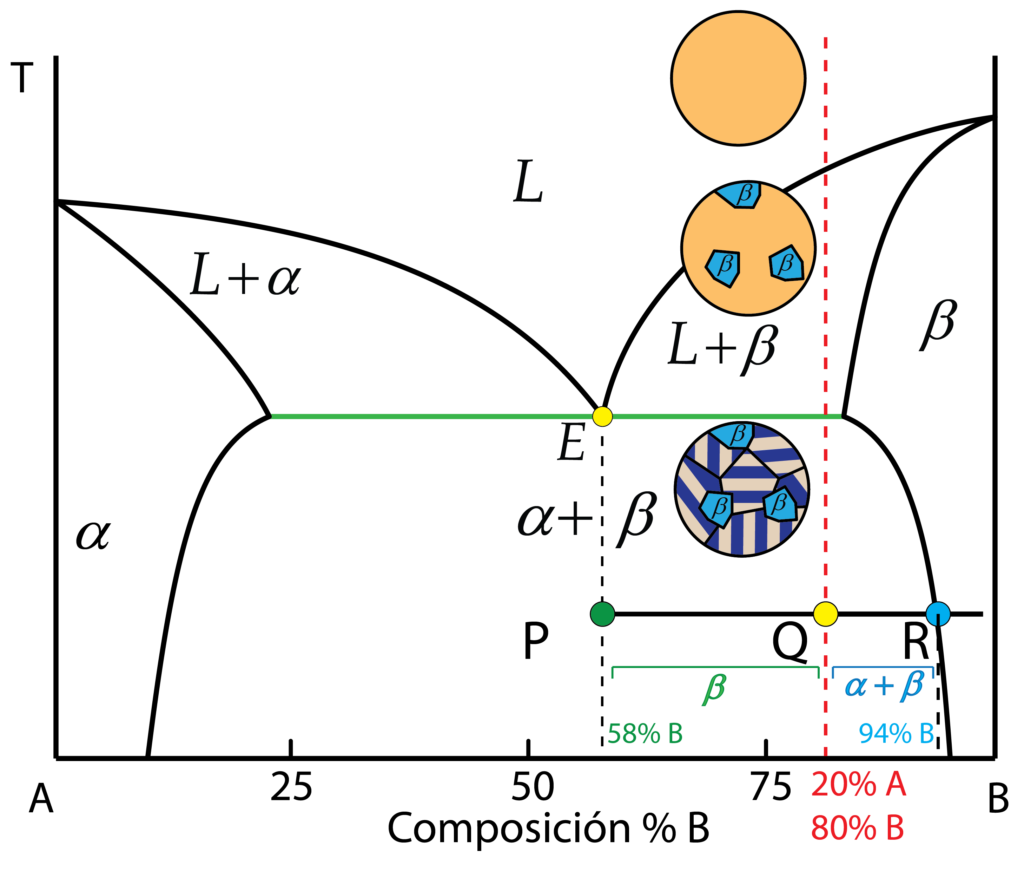
Seleccionemos como ejemplo una aleación con el 20% de A y 80% de B a una temperatura de 200 ºC. Se encuentra en la región bifásica \alpha+\beta, y como durante el enfriamiento se ha cruzado la transformación eutéctica, encontraremos una microestructura típica de una aleación hipereutéctica. Tendremos una matriz eutéctica, y granos dispersos de \beta proeutéctico.
Para obtener los porcentajes de cada uno se trazan los segmentos horizontales PQ y QR, hasta cortar con la línea discontinua que marca la composición eutéctica (P) y con la línea de solvus que marca el límite de solubilidad de \beta (R).
Bajando verticalmente hasta el eje x, leemos cual es la composición para los puntos P y R, obteniendo 58% de B y 94% de B, respectivamente.
Para obtener la masa relativa de eutéctica dividimos el segmento QR entre el segmento PR:
{M_{\alpha + \beta }} = \dfrac{{QR}}{{PR}} = \dfrac{{94 – 80}}{{94 – 58}} = 0,39 \to 39\%
Para obtener la masa relativa de \beta proeutéctico dividimos el segmento PQ entre PR:
{M_\beta } = \dfrac{{PQ}}{{PR}} = \dfrac{{80 – 59}}{{94 – 58}} = 0,61 \to 61\%
Si queréis ampliar un poco más vuestros conocimientos sobre este tipo de diagramas de equilibrio os animo a ver el siguiente vídeo donde se detallan todos estos conceptos con animaciones!!
