En este artículo explicamos cómo resolver vigas hiperestáticas fácilmente, aplicando el método de superposición y la carga unidad. Este método es el más sencillo para vigas con menos de tres reacciones redundantes. Además, al final del artículo tenéis un vídeo con animaciones y más información.
1. Grado de hiperestaticidad
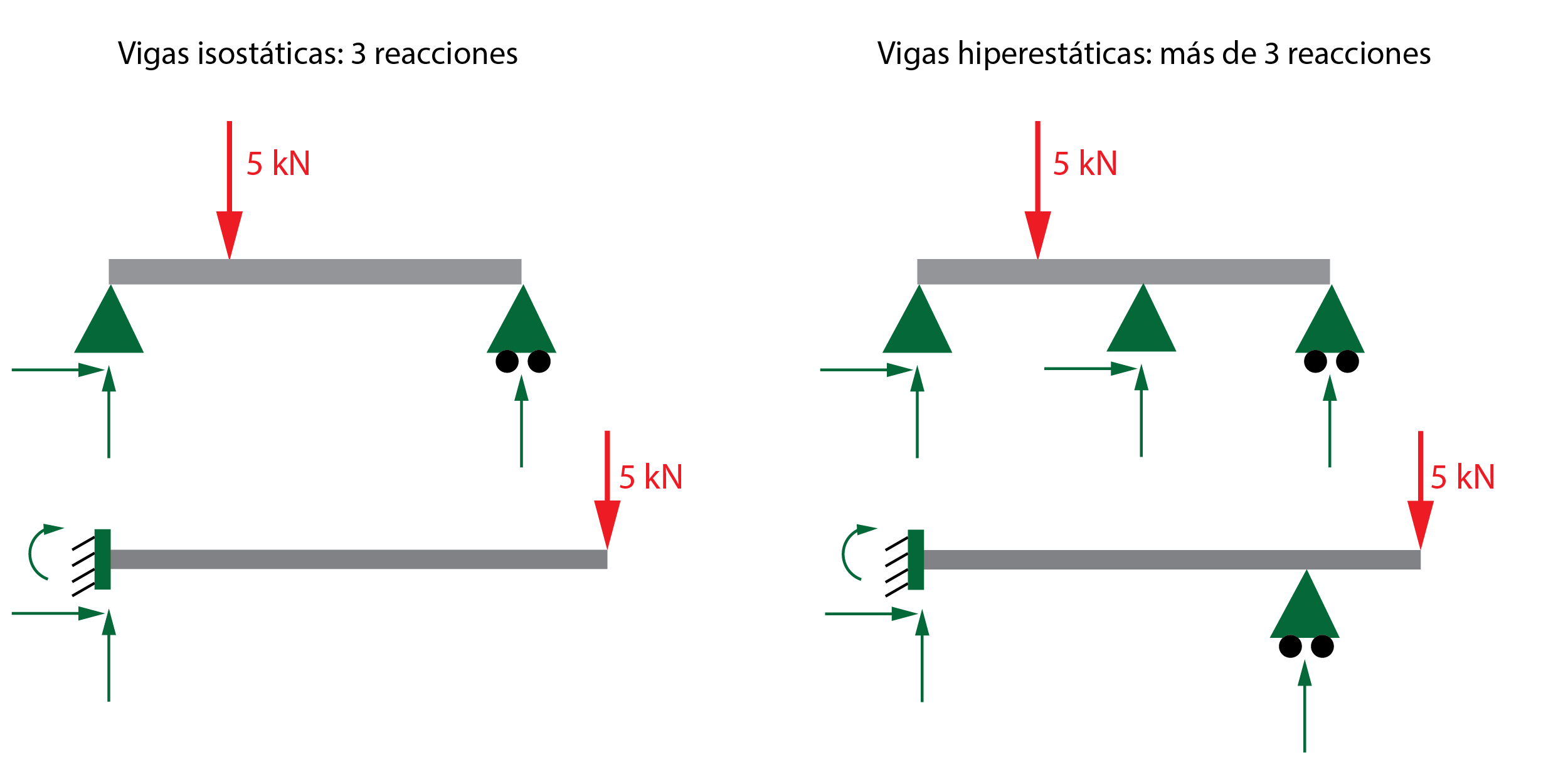
Las vigas (y las estructuras) pueden clasificarse en isostáticas e hiperestáticas. Una viga será isostática si es posible realizar su análisis estático aplicando las ecuaciones de equilibrio, obteniendo las reacciones en los apoyos directamente. Si se trata de un análisis plano, hay tres ecuaciones de equilibrio (suma de fuerzas horizontales y verticales y suma de momentos), por lo que, para que el sistema tenga solución, la viga debe tener tres incógnitas. Es decir, habrá tres reacciones que calcular. Si necesitáis más información previa sobre el método de resolución de vigas, tenéis este artículo.
Nota: esto puede variar en vigas con rótulas, por ejemplo, que añaden ecuaciones adicionales.
Por lo general, si el número de reacciones en los apoyos de la viga es superior a 3, la viga será hiperestática. El grado de hiperestaticidad será mayor conforme aumente el número de reacciones redundantes. Por ejemplo: una viga con 5 reacciones tendrá 2 grados de hiperestaticidad (5-3=2). Estos casos no pueden resolverse directamente, debiendo utilizar métodos con pasos adicionales para su cálculo. En el caso de este artículo aplicaremos el método de superposición y la carga unidad. También puede interesaros el método de pendiente-deflexión.
2. Método de superposición en vigas
El método de superposición. Se trata de una herramienta de gran utilidad aplicable a cualquier tipo de estructura, que permite dividir un caso complejo de cálculo en la suma de casos más sencillos. Las reacciones, leyes y diagramas de la viga original se obtendrán como suma de los casos más simples.
Para la resolución de vigas hiperestáticas, el método es muy sencillo, únicamente hay que dividir la viga original es una viga con las cargas reales, y tantas vigas sencillas adicionales como grados de hiperestaticidad existan en el caso real. Vamos a entenderlo mejor con un ejemplo.
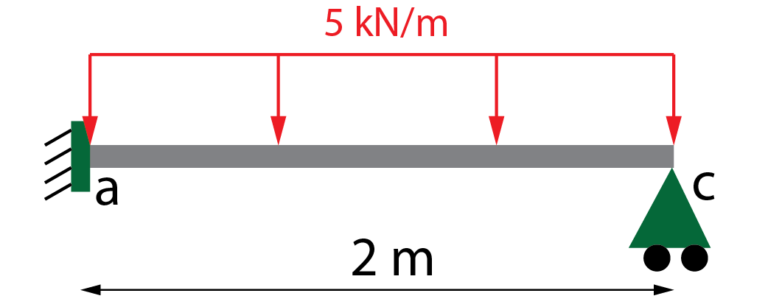
Obtener las reacciones en los apoyos, las leyes de esfuerzos y los diagramas de esfuerzos para la siguiente viga hiperestática.
3. Aplicación del método de superposición
La viga tiene un apoyo empotrado (A) y un apoyo deslizante (C). En total, hay 4 reacciones y 3 ecuaciones estáticas, por lo que se trata de una viga con un grado de hiperestaticidad. Sobra una de las reacciones para poder realizar el cálculo.
Aplicando el método de superposición, dividiremos la viga en suma de dos estados isostáticos:
- Estado 0: debe tener siempre todas las cargas reales. Como tiene que ser isostático (para poder calcularlo), hay que eliminar una reacción. En este caso, lo más sencillo es eliminar el apoyo deslizante. Así es una viga empotrada-libre, con 3 reacciones.
- Estado I: correspondiente a la reacción que se ha eliminado (Rcy). Es una viga que igual tipología que el estado 0 (empotrada-libre), sin cargas reales aplicadas. Únicamente tiene aplicada la reacción Rcy (como si fuera una carga) en la posición del apoyo. El sentido de aplicación es libre. El cálculo posterior determinará el signo de la reacción.

Nota: en caso de más grados de hiperestaticidad, se añadirían estados siguiendo el mismo método para cada reacción eliminada en la viga hiperestática para hacerla isostática.
4. Determinación de las ecuaciones de compatibilidad
El método de superposición ha permitido dividir la viga hiperestática en dos estados isostáticos, hasta aquí todo bien. Sin embargo, sigue existiendo un problema, el estado I tiene como fuerza aplicada Rcy, cuyo valor es desconocido, por lo que no puede resolverse todavía.
Los pasos a seguir son los siguientes:
- Extraer las fuerzas (reacciones) de los estados adicionales multiplicando fuerza de la viga (sí, sé que suena muy raro, pero lo vais entender).
- Para que siga manteniéndose la equivalencia inicial, los estados adicionales tendrán únicamente una carga unidad (fuerza o momento unidad, dependiendo de la reacción). Esta carga unidad, multiplicada por la reacción de fuera de la viga, es igual a lo que inicialmente teníamos.
Ahora, según el método de superposición, la viga hiperestática inicial se obtiene como suma del estado 0, más la reacción Rcy por el estado I, que es un estado unidad.

Sin embargo, esta igualdad no es completamente cierta:
- La viga hiperestática tiene el movimiento vertical en la sección C impedido.
- El movimiento vertical en la sección C, tanto del estado 0 como del estado I, es posible, ya que no hay apoyo que lo restrinja.
Es necesario añadir una ecuación de compatibilidad, que defina un desplazamiento cero en dirección vertical para la sección C. Esta ecuación indica que la suma del desplazamiento vertical en C en el estado 0 y el desplazamiento en el estado I, multiplicado por Rcy debe ser igual a cero.
\delta _y^{C0} + Rcy \cdot \delta _y^{CI} = 0
Esta ecuación es necesaria para resolver el problema y será la que permita obtener la reacción redundante Rcy. Es la ecuación número 4, correspondiente a las 4 reacciones del problema.
Una vez esté resuelta, y Rcy calculado, el resto del problema será muy sencillo.
Nota: en problemas con mayor grado de hiperestaticidad, aparecerá una ecuación de compatibilidad por cada reacción redundante.
5. Aplicación del método de la carga unidad
Ahora bien, la ecuación de compatibilidad conlleva el cálculo del desplazamiento vertical en C para los estados 0 y I. Sin embargo, esto no supone ningún inconveniente si hacemos uso del método de la carga unidad o carga ficticia. Si no conocéis este método, aquí tenéis un artículo previo sobre el mismo.
Según el método de la carga unidad, el desplazamiento (o giro) en una sección de la viga se obtiene con la siguiente fórmula, que depende de las leyes de momento flector de la viga para dos estados: un estado real y un estado ficticio, con una única carga unidad situada en la sección donde quiere obtenerse el desplazamiento (o giro).

\delta = \int_0^L {\dfrac{{{M_{real}} \cdot {M_{ficticio}}}}{{EI}}dx}
La ventaja de combinar el método de superposición y el método de la carga unidad es que el estado I coincide con el estado ficticio necesario para obtener el desplazamiento vertical en C. Esto siempre va a ocurrir, cada estado adicional corresponderá con el estado ficticio para la aplicación del método de la carga unidad en la obtención del desplazamiento para su ecuación de compatibilidad.
De este modo, el desplazamiento en C en el estado 0 se obtiene multiplicando los estados 0 y I.
\delta _y^{C0} = \int_0^L {\dfrac{{{M_0} \cdot {M_I}}}{{EI}}dx}
El desplazamiento en el estado I se obtiene multiplicando dicho estado por sí mismo.
\delta _y^{CI} = \int_0^L {\dfrac{{{M_I} \cdot {M_I}}}{{EI}}dx}
La ecuación de compatibilidad resulta
\int_0^L {\dfrac{{{M_0} \cdot {M_I}}}{{EI}}dx} + Rcy \cdot \int_0^L {\dfrac{{{M_I} \cdot {M_I}}}{{EI}}dx} = 0
Como el material y sección de la viga son constantes, y la ecuación está igualada a cero, el módulo elástico, E, y el momento de inercia, I, pueden simplificarse.
\int_0^L {{M_0} \cdot {M_I}dx} + Rcy \cdot \int_0^L {{M_I} \cdot {M_I}dx} = 06. Cálculo de los estados isostáticos
En este instante, ya estamos listos para calcular los estados isostáticos.
Cálculo del estado 0
En primer lugar, se resuelve el estado 0 con las cargas reales, comenzando con el análisis estático de fuerzas y momentos para la obtención de las reacciones.
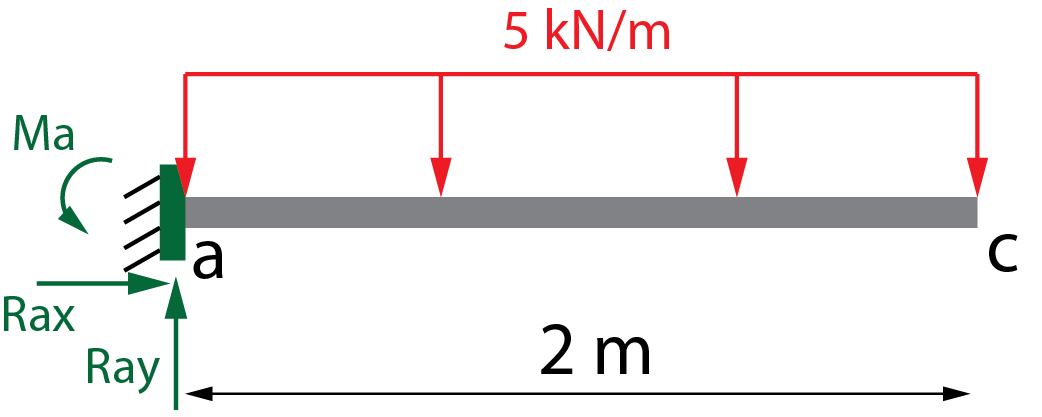
\begin{array}{l}{\sum {{F_x} = 0} \to Rax = 0}\\\\{\sum {{F_y} = 0 \to Ray – 2 \cdot 5 = 0} }\\\\{\sum {M = 0 \to {M_a} – 2 \cdot 5 \cdot 1} = 0}\end{array}
Resolviendo, se obtiene Rax = 0 kN, Ray = 10 kN y Ma = 10 kNm.
Seguidamente, se calculan las leyes de cortante y momento flector. No se calcula la ley de axil ya que no hay cargas ni reacciones en el eje longitudinal de la viga, no existiendo esfuerzo axial en ninguna sección. Para la determinación de las leyes, se parte la viga por una sección antes del extremo final C. La distancia x indica la posición con respecto al inicio de la viga (A). Si tenéis dudas sobre este método de cálculo podéis ojear este artículo.
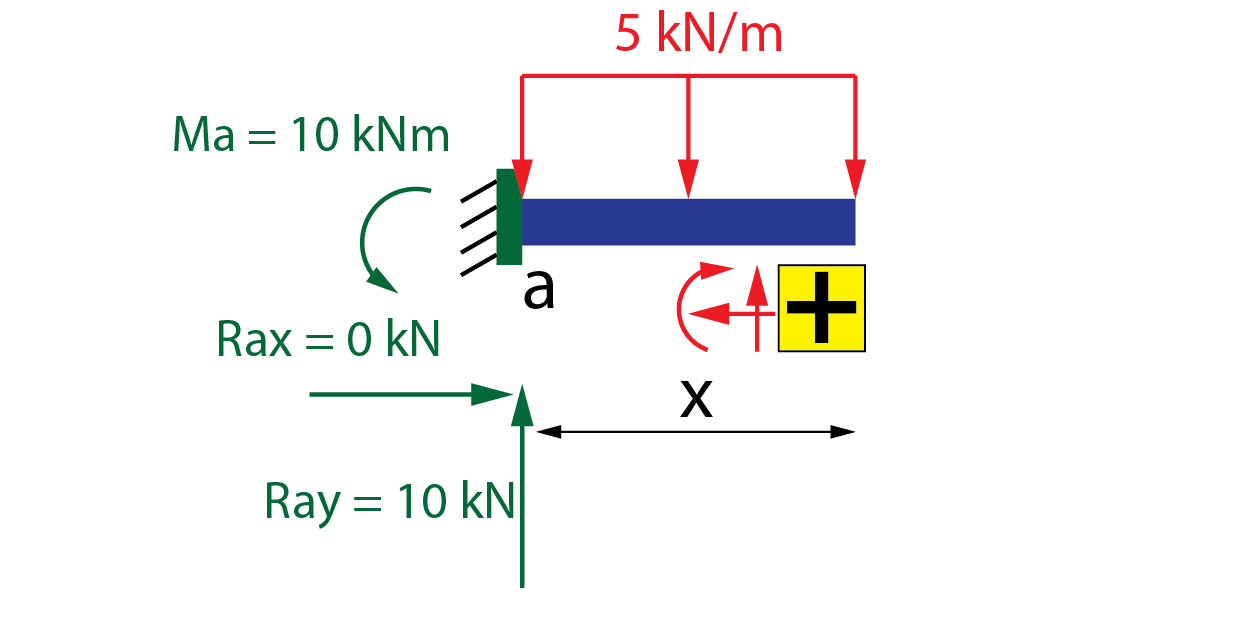
El cortante es generado por la reacción Ray (positivo) y la carga distribuida (negativo).
\left. {V\left( x \right)} \right|_0^2 = Ray – 5 \cdot x
Sustituyendo, resulta
\left. {V\left( x \right)} \right|_0^2 = 10 – 5 \cdot x\;kN
El momento flector es generado por la reacción Ray (positivo), la carga distribuida (negativo) y el momento Ma (negativo).
\left. {M\left( x \right)} \right|_0^2 = Ray \cdot x – 5 \cdot x \cdot \dfrac{x}{2} – Ma
Sustituyendo, resulta
\left. {M\left( x \right)} \right|_0^2 = – \dfrac{{5{x^2}}}{2} + 10x – 10\;kNm
Cálculo del estado I
Para resolver el estado I se opera de manera idéntica, comenzando por el balance estático para obtener las reacciones en los apoyos.

\begin{array}{l}{\sum {{F_x} = 0} \to Rax = 0}\\\\{\sum {{F_y} = 0 \to Ray+1 = 0} }\\\\{\sum {M = 0 \to {M_a} + 2 \cdot 1} = 0}\end{array}
Resolviendo, se obtiene Rax = 0, Ray = -1 y Ma = -2 m. Es importante recalcar que la carga aplicada no tiene unidades. Esto afecta a las unidades de las reacciones: las fuerzas en los apoyos son adimensionales, y el momento tiene unidades de longitud (m).
A continuación, se obtienen las leyes de esfuerzo cortante y momento flector, partiendo la viga por una sección antes del apoyo C. El cortante es generado por la reacción Ray (positivo).
El cortante es generado por la reacción Ray (positivo).
\left. {V\left( x \right)} \right|_0^2 = Ray = – 1
El momento flector es generado por la reacción Ray (positivo) y el momento Ma (negativo).
\left. {M\left( x \right)} \right|_0^2 = Ray \cdot x – Ma = – x + 2\;m
Como se ha comentado antes, las unidades en el estado 0 son distintas. El cortante es adimensional y el momento tiene unidades de longitud (m).
7. Cálculo de la reacción Rcy. Resolución de la ecuación de compatibilidad
Ahora que las leyes de momentos en los estados isostáticos son conocidas, es posible resolver la ecuación de compatibilidad. Para ello, hay que calcular las integrales polinómicas, igualando el resultado a cero.
\int_0^L {{M_0} \cdot {M_I}dx} + Rcx \cdot \int_0^L {{M_I} \cdot {M_I}dx} = 0
\int_0^2 {\left( { – \dfrac{{5{x^2}}}{2} + 10x – 10} \right) \cdot \left( { – x + 2} \right)dx} + Rcy \cdot \int_0^2 {{{\left( { – x + 2} \right)}^2}dx = 0}
– 10 + Rcy \cdot \dfrac{8}{3} = 0
Rcy = 3,75\;kN
8. Cálculo de reacciones y leyes de esfuerzo en la viga hiperestática
Conociendo el valor de la reacción redundante Rcy, resolver la viga hiperestática es muy sencillo si hacemos uso del método de superposición y la ecuación de superposición.
La viga hiperestática es suma del estado 0 y el estado I multiplicado por Rcy, por lo que todas las reacciones y leyes cumplirán dicha relación. Esto permite obtener las reacciones y de leyes de la viga hiperestática a partir de los resultados que ya conocemos.
Reacciones en la viga hiperestática
Ray = Ra{y^0} + Rcy \cdot Ra{y^I} = 10 + 3,75 \cdot \left( { – 1} \right) = 6,25\;kN
Ma = M{a^0} + Rcy \cdot M{a^I} = 10 + 3,75 \cdot \left( { – 2} \right) = 2,5\;kNm
Además, Rax = 0 kN y Rcy = 3,75 kN.
Ley de cortante y ley de momento flector en la viga hiperestática
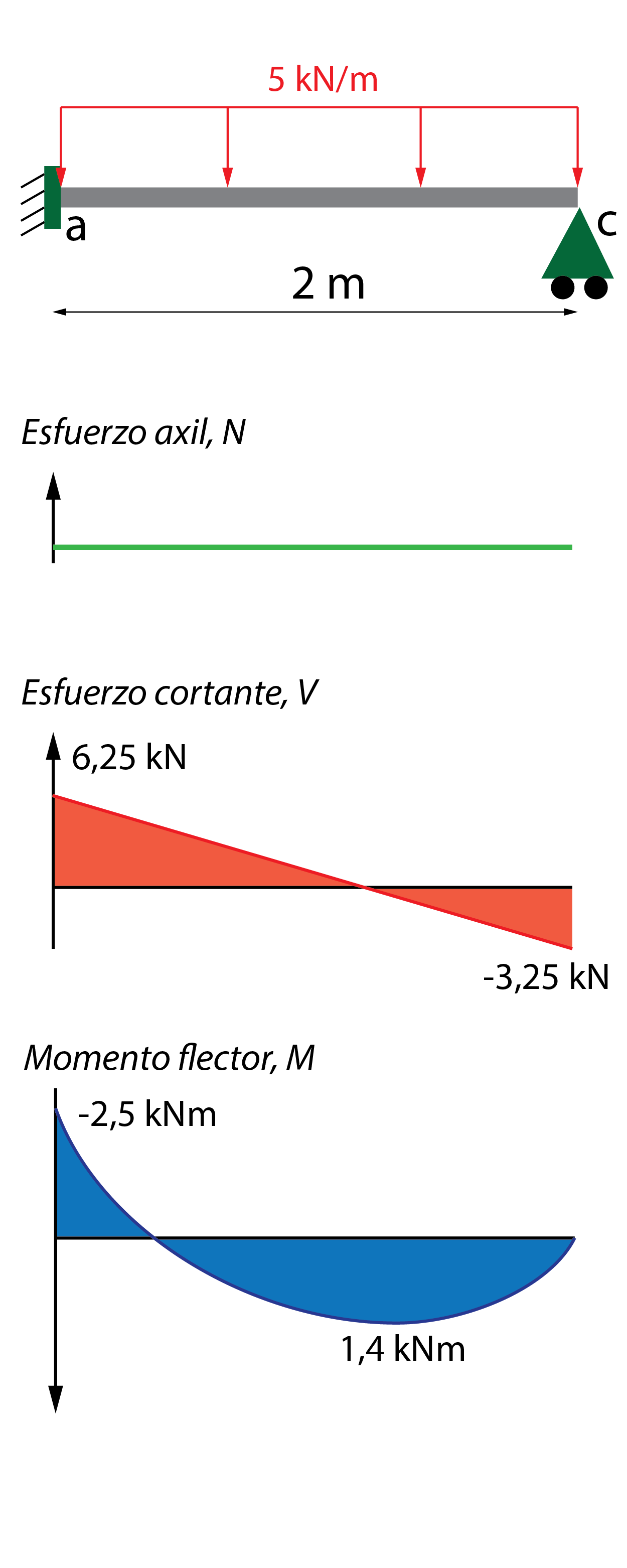
\left. {V\left( x \right)} \right|_0^2 = {V^0} + Rcy \cdot {V^I} = \left( {10 – 5x} \right) + 3,75 \cdot \left( { – 1} \right) = 6,25 – 5x\;kN
\left. {M\left( x \right)} \right|_0^2 = {M^0} + Rcy \cdot {M^I} = \left( { – \dfrac{{5{x^2}}}{2} + 10x – 10} \right) + 3,75 \cdot \left( { – x + 2} \right) = – \dfrac{{5{x^2}}}{2} + 6,25x – 2,5\;kNm
9. Representación de los diagramas de esfuerzo
A partir de las leyes de esfuerzo, se grafican los diagramas siguientes.
Si queréis ampliar un poco más vuestros conocimientos sobre la resolución de vigas hiperestáticas os animo a ver los vídeos siguientes donde hay más ejemplos resueltos!!
