En este artículo explicamos cómo resolver vigas hiperestáticas fácilmente, aplicando el método de pendiente-deflexión Este método es el más sencillo para vigas con más de tres grados de hiperestaticidad. Además, al final del artículo tenéis un vídeo con animaciones y más información. Si estáis empezando con la resolución de vigas hiperestáticas, también puede interesaros conocer el método de superposición.
1. Grado de hiperestaticidad
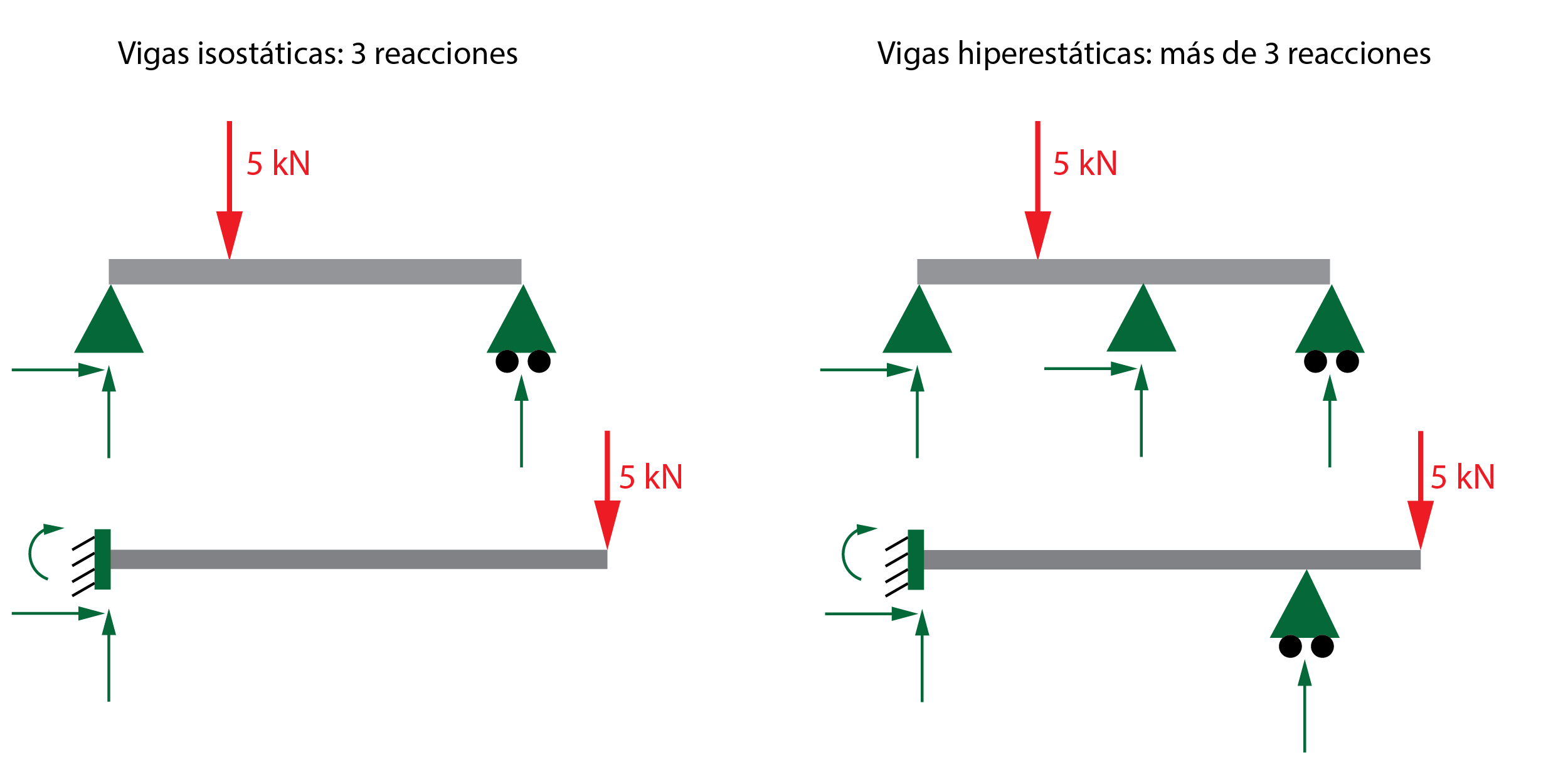
Las vigas (y las estructuras) pueden clasificarse en isostáticas e hiperestáticas. Una viga será isostática si es posible realizar su análisis estático aplicando las ecuaciones de equilibrio, obteniendo las reacciones en los apoyos directamente. Si se trata de un análisis plano, hay tres ecuaciones de equilibrio (suma de fuerzas horizontales y verticales y suma de momentos), por lo que, para que el sistema tenga solución, la viga debe tener tres incógnitas. Es decir, habrá tres reacciones que calcular. Si necesitáis más información previa sobre el método de resolución de vigas, tenéis este artículo.
Nota: esto puede variar en vigas con rótulas, por ejemplo, que añaden ecuaciones adicionales.
Por lo general, si el número de reacciones en los apoyos de la viga es superior a 3, la viga será hiperestática. El grado de hiperestaticidad será mayor conforme aumente el número de reacciones redundantes. Por ejemplo: una viga con 5 reacciones tendrá 2 grados de hiperestaticidad (5-3=2). Estos casos no pueden resolverse directamente, debiendo utilizar métodos con pasos adicionales para su cálculo. Cuando el grado de hiperestaticidad es inferior a 3, normalmente es aconsejable aplicar el método de superposición y la carga unidad. Para vigas con un grado de hiperestaticidad mayor, resulta más coherente utilizar el método de pendiente-deflexión que explicamos a continuación.
2. ¿En qué consiste el método de pendiente-deflexión?
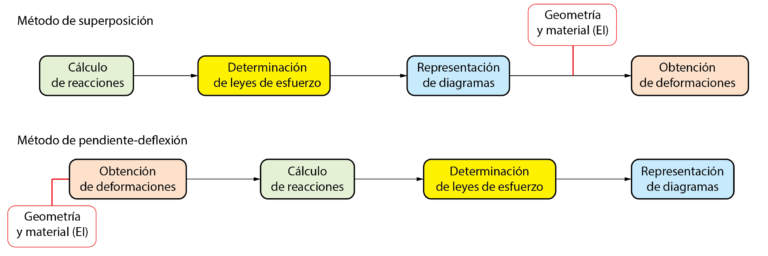
El método de pendiente-deflexión es un método clásico de cálculo de vigas que permite calcular directamente el momento flector, los giros y los desplazamientos en los apoyos de una viga. Esto supone un gran ventaja en aquellas ocasiones donde se busca obtener estos resultados sin necesidad de conocer las reacciones en los apoyos o las leyes de esfuerzo.
La metodología es muy distinta a otros procedimientos, como el método de superposición, ya se calculan las deformaciones para, posteriormente, obtener reacciones y esfuerzos. Normalmente, estamos más habituados a calcular las reacciones en los apoyos en primer lugar, para describir las leyes de esfuerzos en la viga y deducir los desplazamientos y giros en último lugar.
Por lo tanto, el método de pendiente-deflexión en una opción excelente si lo que se busca es conocer las deformaciones en una viga, aunque también puede aplicarse (como veremos a continuación) para calcular una viga hiperestática al completo.
El método de pendiente-deflexión consiste en partir la viga hiperestática en tantos trozos como vanos haya definidos por los apoyos. Recordad que un vano es un tramo de viga entre apoyos.
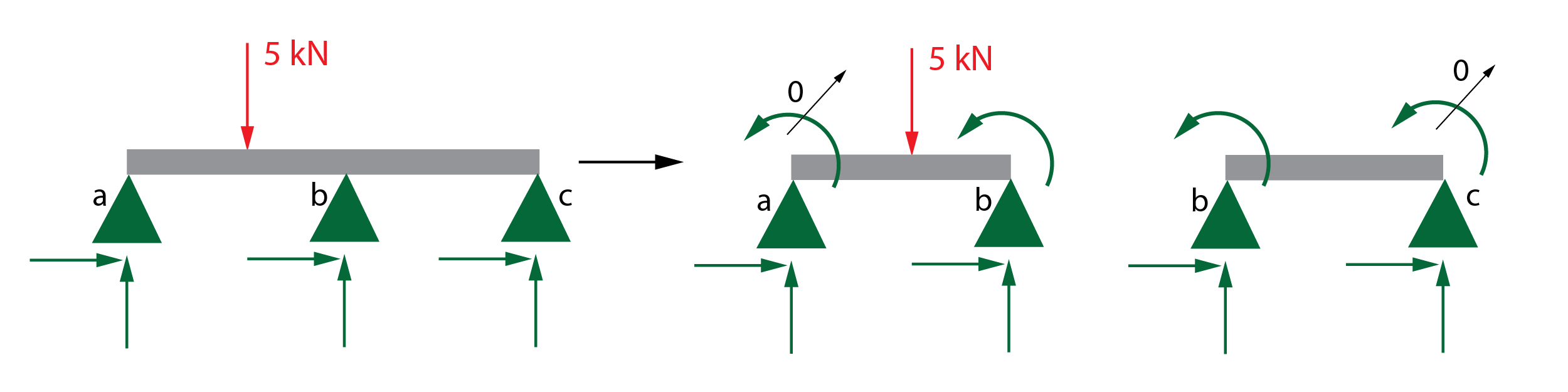
Para que las condiciones del problema, una vez partido, sean las mismas que el original, aparecen unos momentos de giro en los extremos de cada vano, atiendiendo a unas condiciones:
- Si se trata de un apoyo intermedio en la viga hiperestática inicial, siempre aparecerá un momento de giro.
- Si se trata de un apoyo extremo (inicial o final) de la viga hiperestática, solo aparecerá un momento de giro si es un apoyo empotrado. En el caso de apoyos fijos, deslizaderas o voladizos, no existirá momento.
Si nombramos con el subíndice i al extremo inicial del vano, y con el subíndice f al extremo final, la siguientes fórmulas pueden aplicarse para obtener el momento de giro en cada uno de los extremos.
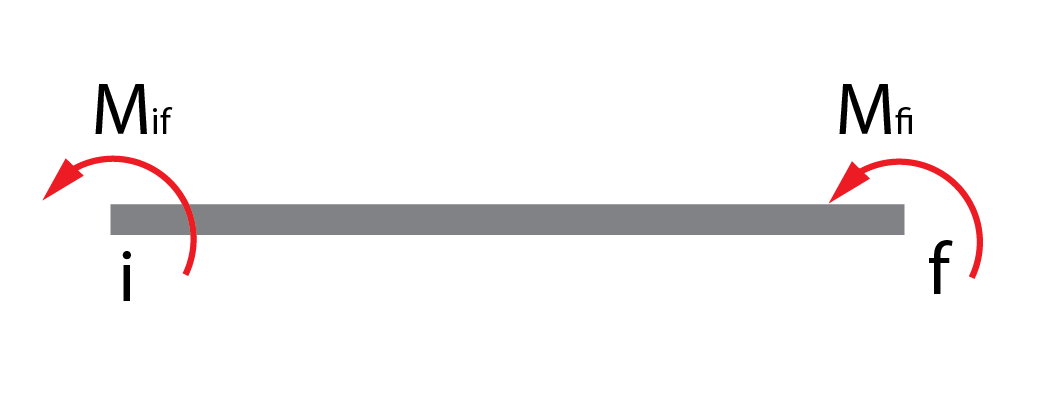
\begin{array}{l}{M_{if}} = \dfrac{{2EI}}{L}\left[ {2{\theta _i} + {\theta _f} – \dfrac{{3\Delta }}{L}} \right]\\\\{M_{fi}} = \dfrac{{2EI}}{L}\left[ {2{\theta _f} + {\theta _i} – \dfrac{{3\Delta }}{L}} \right] \end{array}
Sin entrar en la deducción de las fórmulas, vemos que estas dependen del módulo elástico, E, del material de la viga, y del momento de inercia, I, de la sección. Por lo tanto, al contrario de otros procedimientos, el método de pendiente-deflexión requiere de conocer estos datos a priori para poder aplicarse. El resto de términos son:
- El ángulo de giro en el extremo inicial, \theta_i, y el ángulo de giro en el extremo final, \theta_f. En los apoyos fijos y deslizaderas, el giro está permitido, siendo incógnitas a calcular. En los apoyos empotrados, el giro es nulo.
- El desplazamiento vertical relativo entre los dos apoyos, \Delta. Aquí se tiene en cuenta que alguno de los apoyos pueda desplazarse respecto al otro. Únicamente será incógnita en caso de extremos en voladizo o deslizaderas en dirección vertical.
- El momento de empotramiento perfecto, MP. Los momentos de empotramiento perfecto son aquellos que aparecen en los extremos de una viga biempotrada debido a las cargas aplicadas.
Según el criterio de signos, los momentos M_{if} y M_{fi} se dibujan en sentido antihorario, ya que se toma como positivo. Nota: esto es importante, ya que las tablas de momento perfecto para el extremo final, suelen representar el momento en sentido horario, por lo que es necesario colocarlo con signo negativo en la fórmula.
Aplicando estas fórmulas en cada tramo de la viga, obtendremos relaciones para calcular los momentos y las deformaciones. Para entenderlo mejor, veamos el método aplicado a un ejemplo.
Obtener las reacciones en los apoyos, las leyes de esfuerzo y los diagramas de la siguiente viga hiperestática. E = 210000\, MPa, I = 500\, cm^4.
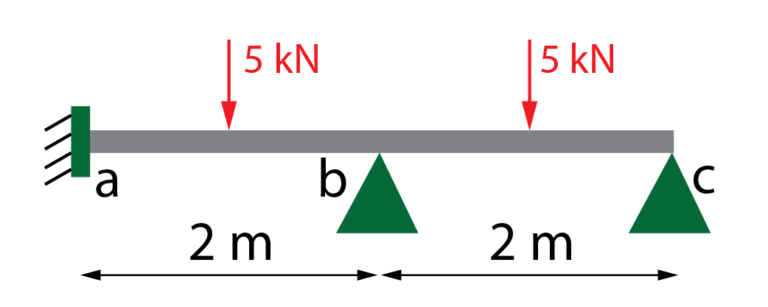
La viga del ejemplo es hiperestática con 4 grados de hiperestaticidad, ya que hay 7 reacciones incógnita y 3 ecuaciones estáticas. Optar por la aplicación del método de pendiente-deflexión es una buena opción.
3. Aplicación de las ecuaciones para determinación de los momentos en los extremos de viga
En primer lugar, es necesario dividir la viga hiperestática en distintos vanos en función de los apoyos. En este caso, resultan 2 vanos, en cuyos extremos aparecerá un momento de giro. Inicialmente, dibujaremos momentos en todos los extremos y en sentido positivo (antihorario).
Mediante las ecuaciones anteriores, se obtendrán relaciones entre las incógnitas del problema: momentos en los extremos, giros y desplazamientos. Para aplicar la ecuación con mayor facilidad, de acuerdo a las unidades del enunciado, tanto E como I serán expresados en kN y m.
\begin{array}{l}E = 210000\;MPa = 2,1 \cdot {10^8}\;kN/{m^2}\\\\I = 500\;c{m^4} = 5 \cdot {10^{ – 6}}\;c{m^4}\end{array}
Así, calculamos el valor del término EI.
EI = 1050\;kN{m^2}
Tramo ab
Se plantean dos ecuaciones, una para cada extremo referidos a los momentos M_{ab} y M_{ba}. En este tramo sabemos que el giro en el extremo a, \theta_{a}=0, ya que se trata de un apoyo empotrado. Por otro lado, como ambos apoyos tienen restringido el desplazamiento vertical (empotramiento y apoyo fijo), \Delta=0.
El momento de empotramiento perfecto se obtiene de la tabla para una viga con una carga puntual en la sección central. De acuerdo con el criterio de signos, el momento en el extremo inicial a es
M{P_a} = \dfrac{{PL}}{8} = \dfrac{{5 \cdot 2}}{8} = 1,25\;kNm
El momento en el extremo final b en la tabla tiene el sentido contrario al planteado como positivo en la resolución del problema, por lo que será un momento negativo
M{P_b} = -\dfrac{{PL}}{8} =- \dfrac{{5 \cdot 2}}{8} =- 1,25\;kNm
Por lo tanto, la ecuación para el extremo a de este vano es
{M_{ab}} = \dfrac{{2EI}}{L}\left[ {2{\theta _a} + {\theta _b} – \dfrac{{3\Delta }}{L}} \right] + M{P_a} = \dfrac{{2EI}}{L}{\theta _b} + 1,25
{M_{ab}} = 1050{\theta _b} + 1,25
Y la ecuación para el extremo b de este vano es
{M_{ba}} = \dfrac{{2EI}}{L}\left[ {2{\theta _b} + {\theta _a} – \dfrac{{3\Delta }}{L}} \right] + M{P_b} = \dfrac{{2EI}}{L} \cdot 2{\theta _b} – 1,25
{M_{ba}} = 2100{\theta _b} – 1,25
Tramo bc
De manera similar, es necesario obtener las dos ecuaciones para los momentos en los extremos del tramo bc de la viga, M_{bc} y M_{cb}.
Como se trata de dos apoyos fijos, sí habrá giro en las secciones b y c, pero no desplazamiento vertical entre apoyos, siendo \Delta=0. Por otro lado, el extremo c es fijo, siendo el final de la barra hiperestática, por lo que no habrá esfuerzo de flexión, siendo M_{cb}=0\,kNm.
Los momentos de empotramiento perfecto, de manera análoga con el tramo ab, son
M{P_b} = \dfrac{{PL}}{8} = \dfrac{{5 \cdot 2}}{8} = 1,25\;kNm
M{P_c} = -\dfrac{{PL}}{8} = -\dfrac{{5 \cdot 2}}{8} =- 1,25\;kNm
Con todo esto, la ecuación para el extremo b de este vano es
{M_{bc}} = \dfrac{{2EI}}{L}\left[ {2{\theta _b} + {\theta _c} – \dfrac{{3\Delta }}{L}} \right] + M{P_b} = \dfrac{{2EI}}{L}\left[ {2{\theta _b} + {\theta _c}} \right] + 1,25
{M_{bc}} = 2100{\theta _b} + 1050{\theta _c} + 1,25
La ecuación para el extremo c es
{M_{cb}} = \dfrac{{2EI}}{L}\left[ {2{\theta _c} + {\theta _b} – \dfrac{{3\Delta }}{L}} \right] + M{P_c} = \dfrac{{2EI}}{L}\left[ {2{\theta _c} + {\theta _b}} \right] – 1,25
0 = 1050{\theta _b} + 2100{\theta _c} – 1,25
4. Resolución del sistema
Tenemos un sistema de ecuaciones lineales con 4 ecuaciones (2 para cada vano) y un total de 5 incógnitas:
- Los momentos M_{ab}, M_{ba} y M_{bc}.
- Los giros \theta_{b} y \theta_{c}.
Sin embargo, el momento flector en la sección b únicamente puede tener un valor, aunque aparezcan dos distintos al partir la viga en dos tramos. Para que exista el equilibrio, ambos momentos deben ser iguales y de sentido contrario (basta con voltear el momento M_{bc}), siendo M_{bc}=-M_{ba}.
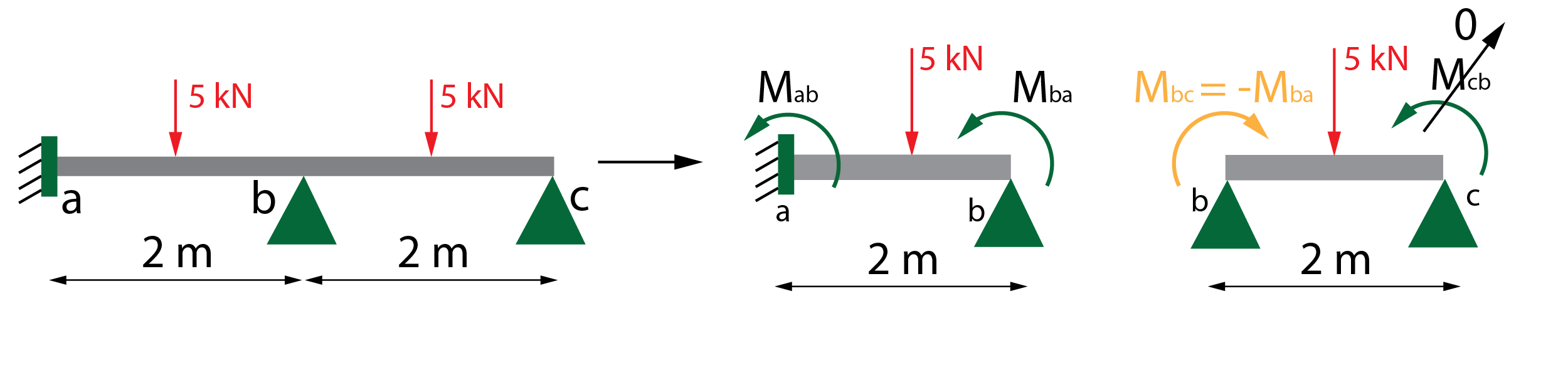Esta duplicidad en los momentos aparecerá siempre en los apoyos intermedios de una viga, cumpliéndose la igualdad. Finalmente, el sistema de ecuaciones a resolver es
\left\{ {\begin{array}{l}{{M_{ab}} = 1050{\theta _b} + 1,25}\\\\{{M_{ba}} = 2100{\theta _b} – 1,25}\\\\{ – {M_{ba}} = 2100{\theta _b} + 1050{\theta _c} + 1,25}\\\\{0 = 1050{\theta _b} + 2100{\theta _c} – 1,25}\end{array}}\right.
Como se trata de un sistema lineal de 4 ecuaciones con 4 incógnitas, lo más cómodo es resolverlo en forma matricial. Para ello, se reescriben las ecuaciones dejando las incógnitas en un lado y los números en otro y se expresa como
\left( {\begin{array}{c}1&0&{ – 1050}&0\\0&1&{ – 2100}&0\\0&{ – 1}&{ – 2100}&{ – 1050}\\0&0&{ – 1050}&{ – 2100} \end{array}} \right) \cdot \left( {\begin{array}{c}{{M_{ab}}}\\{{M_{ba}}}\\{{\theta _b}}\\{{\theta _c}}\end{array}} \right) = \left( {\begin{array}{c}{1,25}\\{ – 1,25}\\{1,25}\\{ – 1,25}\end{array}} \right)
Mediante la matriz inversa se obtiene
\left( {\begin{array}{c}{{M_{ab}}}\\{{M_{ba}}}\\{{\theta _b}}\\{{\theta _c}}\end{array}} \right) = \left( {\begin{array}{c}{1071,5\;Nm}\\{ – 1607\;Nm}\\{ – 0,00017\;rad}\\{0,00068\;rad} \end{array}}\right)
Se han obtenido los momentos en las secciones a y b, y el giro en las secciones b y c.
5. Obtención de las reacciones en los apoyos
Una vez calculados los resultados anteriores, estamos en disposición de obtener las reacciones en los apoyos. Si únicamente se tiene interés en obtener deformaciones, el problema acabaría aquí.
Para obtener las reacciones hay que realizar el balance estático (suma de fuerzas y momentos) en cada vano de viga. Como no hay cargas horizontales, las reacciones en esa dirección son nulas. En la sección b, se obtendrán dos reacciones (una para cada vano), siendo la suma la reacción en la viga hiperestática.
Tramo ab
En primer lugar se plantea el equilibrio de momentos en la sección b, tomando los momentos en sentido horario como positivos (se puede tomar el criterio inverso) e igualando a cero.
2 \cdot Ray – 1 \cdot 5000 + 1607 – 1071,5 = 0
Ray = 2230\;N
La reacción Rb_{1} se obtiene del balance de fuerzas verticales
Ray + R{b_1} – 5000 = 0
R{b_1} = 2770\;N
Tramo bc
De manera similar, se obtiene la reacción Rb_2 mediante el equilibrio de momentos en la sección c
2 \cdot R{b_2} – 1 \cdot 5 – 1607 = 0
R{b_2} = 3300\;N
A partir del equilibrio de fuerzas verticales se obtiene la reacción Rcy
R{b_2} + Rcy – 5000 = 0
Rcy = 1690\;N
Por último, se suman las reacciones Rb_1 y Rb_2, obteniendo las reacciones en la viga hiperestática
\begin{array}{c}{Ray = 2230\;N}\\\\{{M_a} = 1071,5\;Nm}\\\\{Rb = 6100\;N}\\\\{Rcy = 1690\;N}\end{array}
6. Determinación de leyes de esfuerzo
Seguidamente, se calculan las leyes de cortante y momento flector. No se calcula la ley de axil ya que no hay cargas ni reacciones en el eje longitudinal de la viga, no existiendo esfuerzo axial en ninguna sección. Si tenéis dudas sobre este método de cálculo podéis ojear este artículo.
Esfuerzo cortante
\begin{array}{l}\left. {V\left( x \right)} \right|_0^1 = 2,23\;kN\\\\\left. {V\left( x \right)} \right|_1^2 = 2,23 – 5 = – 2,77\;kN\\\\\left. {V\left( x \right)} \right|_2^3 = 2,23 – 5 + 6,1 = 3,33\;kN\\\\\left. {V\left( x \right)} \right|_3^4 = 2,23 – 5 + 6,1 – 5 = – 1,69\;kN\end{array}
Momento flector
\begin{array}{l}\left. {M\left( x \right)} \right|_0^1 = 2,23x – 1,07\;kNm\\\\\left. {M\left( x \right)} \right|_1^2 = 2,23x – 1,07 – 5 \cdot \left( {x – 1} \right)\\\\= – 2,77x + 3,93\;kNm\\\\\left. {M\left( x \right)} \right|_2^3 = 2,23x – 1,07 – 5 \cdot \left( {x – 1} \right) + 6,1 \cdot \left( {x – 2} \right)\\\\= 3,33x – 8,27\;kNm\\\\\left. {M\left( x \right)} \right|_3^4 = 2,23x – 1,07 – 5 \cdot \left( {x – 1} \right) + 6,1 \cdot \left( {x – 2} \right) – 5 \cdot \left( {x – 3} \right)\\\\= – 1,69x + 6,73\;kNm\end{array}
7. Representación de los diagramas de esfuerzo
A partir de las leyes de esfuerzo, se grafican los diagramas siguientes.
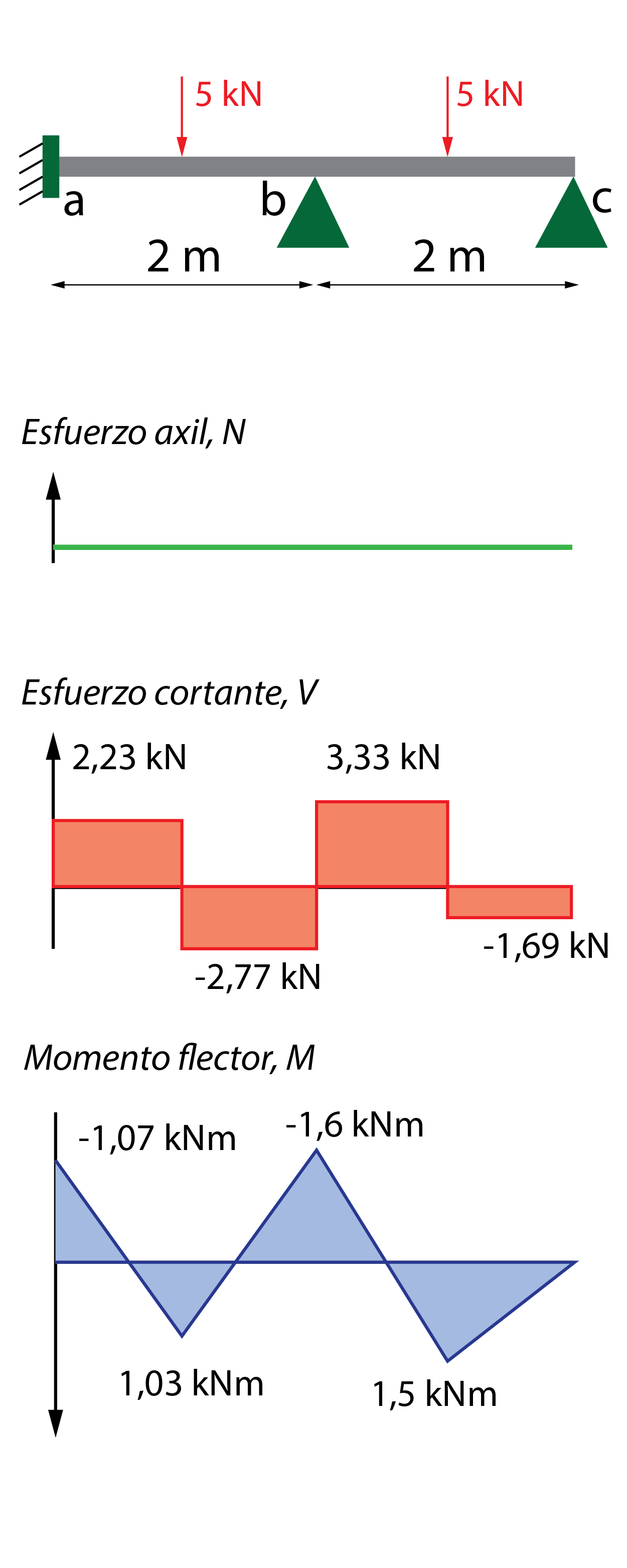
Si queréis ampliar un poco más vuestros conocimientos sobre la resolución de vigas hiperestáticas os animo a ver este vídeo donde hay más ejemplos resueltos!!