En este artículo explicamos cómo realizar el cálculo de pórticos isostáticos para obtener las reacciones en los apoyos, las leyes de esfuerzo y los diagramas de esfuerzo. Además, al final del artículo tenéis un vídeo con animaciones y más información.
1. ¿Qué es un pórtico?
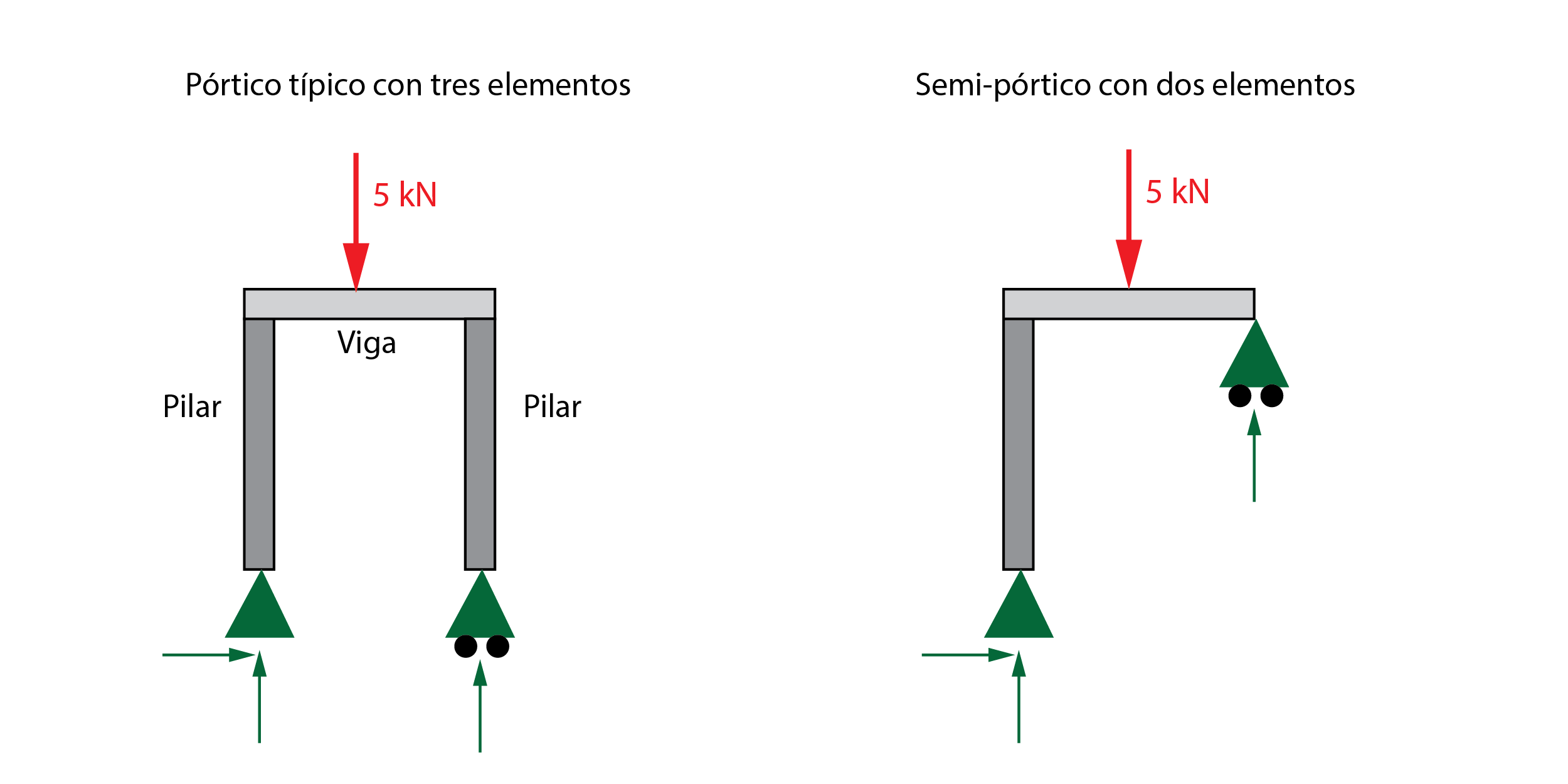
Un pórtico es una estructura formada por tres vigas colocadas de manera perpendicular. Así, dos vigas quedan situadas en vertical, lo que se conoce habitualmente como pilares del pórtico. La tercera viga se coloca horizontalmente sobre los pilares, conocida como viga o dintel. También existen otros tipos de pórtico, como un pórtico formado por un pilar y un dintel, estando este apoyado o empotrado en el otro extremo, pero son casos más específicos.
En este artículo veremos el cálculo de pórticos isostáticos de tres elementos, que es lo más habitual. Al igual que ocurre con las vigas, un pórtico será isostático si se desconocen 3 reacciones incógnita, ya que se conocen 3 ecuaciones estáticas, pudiendo resolver el sistema. Si, debido a los apoyos, el número de reacciones es superior, el pórtico será hiperestático, lo que requiere de etapas y pasos adicionales de cálculo.
2. Metodología para el cálculo de pórticos
Para resolver un pórtico isostático hay que seguir el siguiente procedimiento:
- Primero es necesario obtener las reacciones en los apoyos (al igual que se realiza en una viga isostática). Para ello, se lleva a cabo el balance estático global del pórtico a partir de las 3 ecuaciones estáticas (equilibrio de fuerzas y momentos).
- Seguidamente, se identifican los ejes locales de cada elemento del pórtico. En el caso de la viga horizontal, estos ejes locales coincidirán con los ejes x e y globales. Sin embargo, los elementos verticales tendrán asociado un giro.
- Se obtienen las leyes de esfuerzo (axil, cortante y flector) del primer elemento del pórtico. Lo más común es comenzar calculando el pilar izquierdo.
- A partir de las leyes se calculan los esfuerzos axil, cortante y flector en el extremo final del elemento. En el caso del pilar izquierdo, el extremo final es la cabeza del pilar (punto más alto en unión con la viga).
- Los esfuerzos calculados al final del pilar se «transfieren» al extremo inicial de la viga.
- Se obtienen las leyes de esfuerzos en la viga y, de nuevo, se calculan los esfuerzos en su extremo final. Siguiendo el recorrido de izquierda a derecha en el pórtico, el extremo final es el extremo derecho de la viga.
- Los esfuerzos al final de la viga se «transfieren» al extremo inicial de pilar derecho, es decir, al extremo unido a la viga.
- Por último, se obtienen las leyes de esfuerzo en este pilar. Con todas las leyes ya estamos en disposición de representar los diagramas de esfuerzo.
3. Aplicación de la metodología para el cálculo de pórticos
Esta metodología general para el cálculo de pórticos queda mucho mejor explicada si la ponemos en práctica con el ejemplo siguiente.
Obtener las reacciones en los apoyos, las leyes de esfuerzo y los diagramas de esfuerzo en el siguiente pórtico isostático.
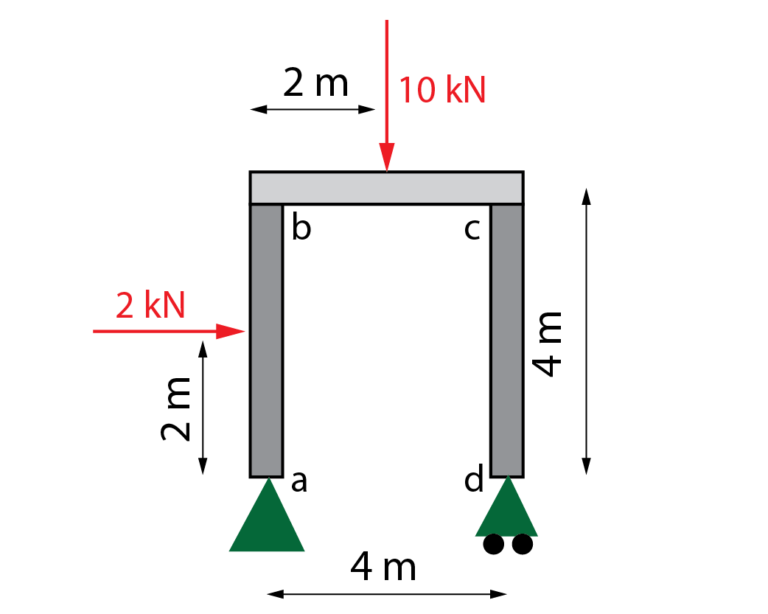
4. Obtención de las reacciones en los apoyos
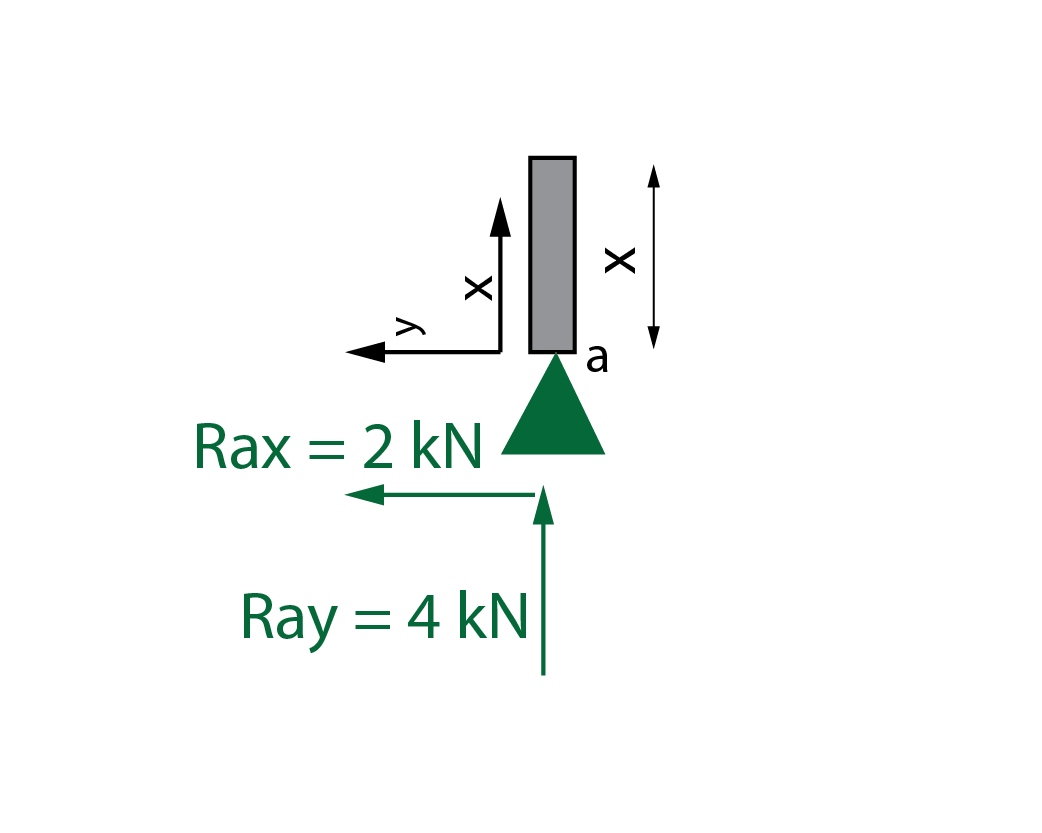
En primer lugar calculamos las reacciones en los apoyos, resolviendo el balance estático. Utilizamos las tres ecuaciones, equilibrio de fuerzas horizontales, equilibrio de fuerzas verticales y equilibrio de momentos en un punto, por ejemplo en el apoyo a. Se ha tomado como positivo el sentido de giro antihorario en la ecuación de momentos.
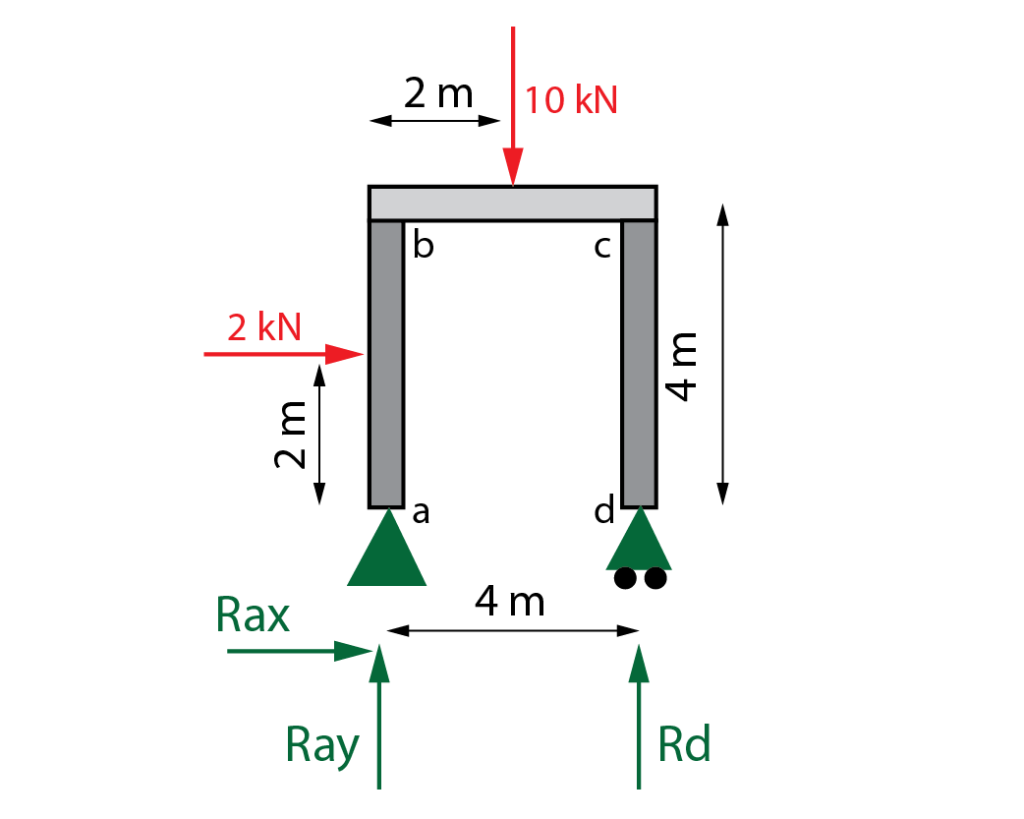
Obtenemos Rax=-2\,kN, Ray=4\,kN y Rd=6\,kN.
5. Determinación de leyes de esfuerzo
A partir de las reacciones en los apoyos, ya es posible obtener las leyes de esfuerzo en cada elemento del pórtico. Comenzaremos por el pilar a-b.
Leyes de esfuerzo en el pilar a-b
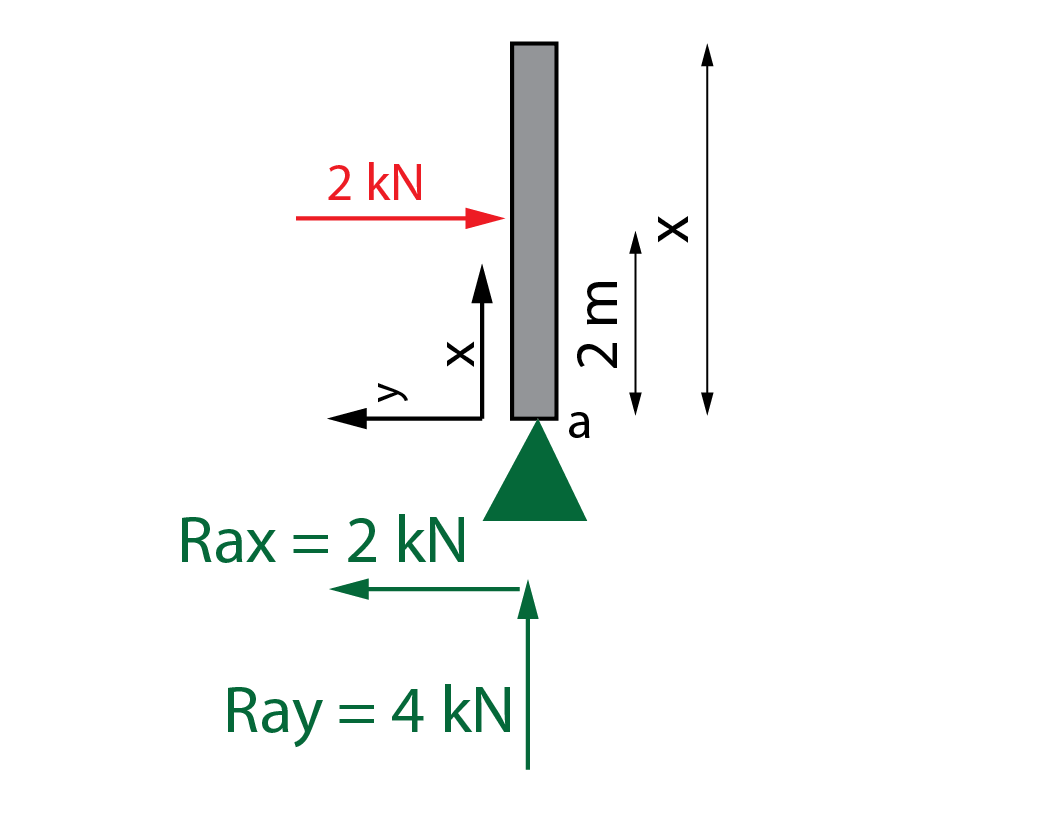
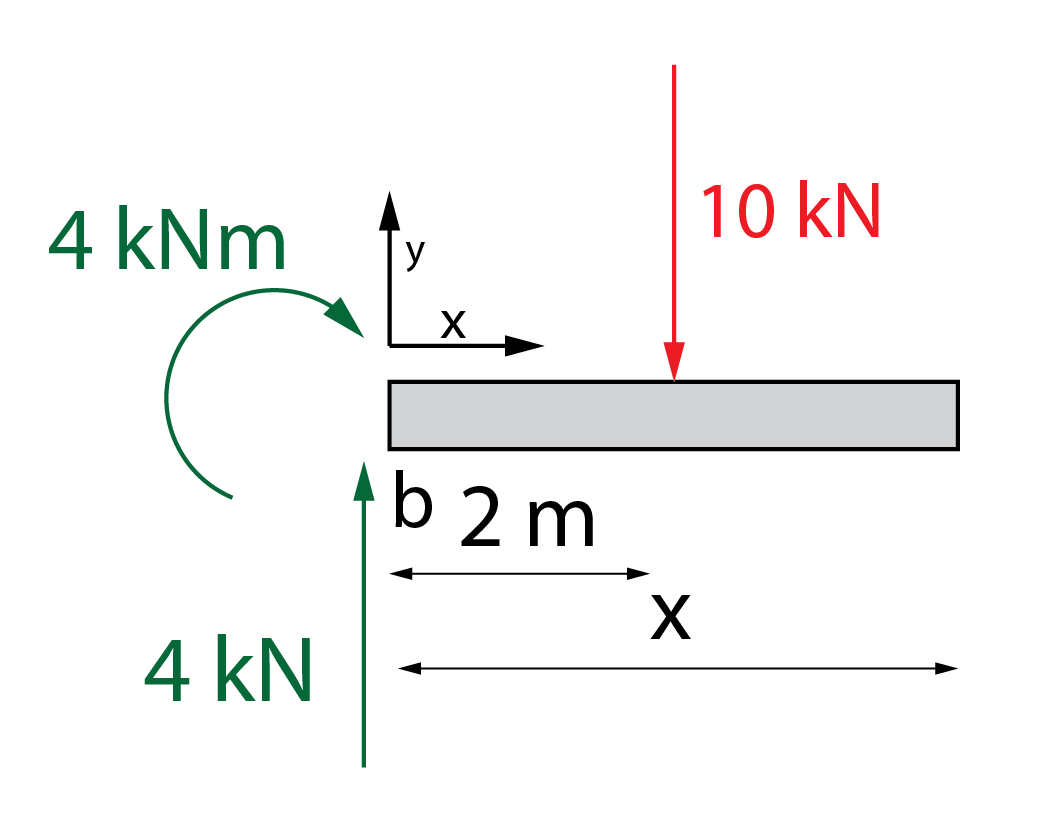
En primer lugar, hay que situar y determinar los ejes x e y. Como el elemento está girado, los ejes giran 90º, quedando el eje x en vertical y el eje y en horizontal. Recuérdese que estos son los ejes locales. El eje x marca la dirección longitudinal del pilar, mientras que el eje y indica la dirección perpendicular. De acuerdo con estos ejes se obtienen los esfuerzos axial, cortante y flector en toda la longitud del pilar utilizando el método habitual.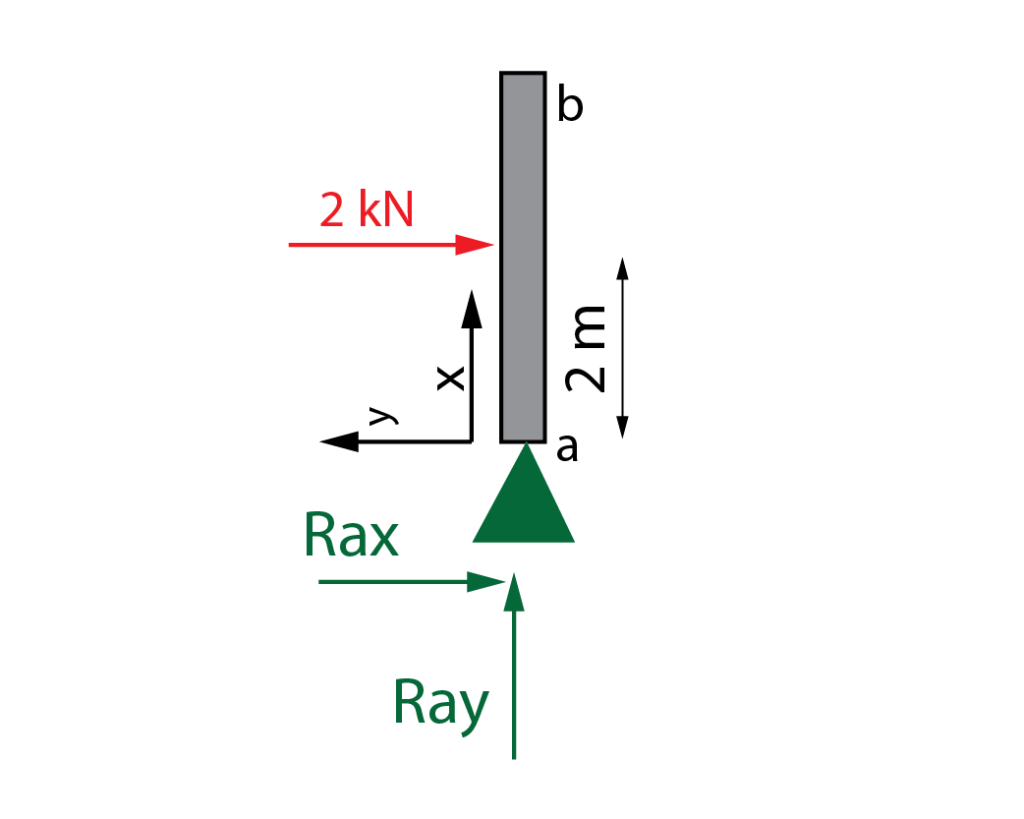
Como hay una carga puntual en mitad del pilar, las leyes estarán partidas en dos tramos, el tramo entre 0 m y 2 m y el tramo entre 2 m y 4 m. Siguiendo el criterio de signos establecido para cada esfuerzo, las leyes en cada tramo son
\begin{array}{l}\left. {N\left( x \right)} \right|_0^2 = – 4\;kN\\\\\left. {V\left( x \right)} \right|_0^2 = 2\;kN\\\\\left. {M\left( x \right)} \right|_0^2 = 2x\;kNm\end{array}
\begin{array}{l}\left. {N\left( x \right)}\right|_2^4 = – 4\;kN\\\\\left. {V\left( x \right)} \right|_2^4 = 2 – 2 = 0\;kN\\\\\left. {M\left( x \right)} \right|_2^4 = 2x – 2\left( {x – 2} \right) = 4\;kNm\end{array}
Con las leyes obtenidas para el segundo tramo, calculamos los esfuerzos en el extremo final, es decir, x = 4 m. En este caso, como las leyes son constantes, es muy sencillo y no es necesario ni siquiera sustituir la x.
\begin{array}{l}N\left( 4 \right) = – 4\;kN\\\\V\left( 4 \right) = 0\;kN\\\\M\left( 4 \right) = 4\;kNm\end{array}
Estos esfuerzos deben ser transferidos a la viga, teniendo las siguientes consideraciones:
- El esfuerzo axial de -4 kN, siguiendo el criterio de signos es una fuerza en dirección vertical hacia abajo. Esta fuerza influirá en el esfuerzo cortante de la viga, al estar girada 90º respecto del pilar.
- No hay esfuerzo cortante, por lo que no se transfiere ninguna carga en dirección axial a la siguiente viga.
- El momento flector es positivo. Según el criterio es sentido horario, que será transferido a la viga.
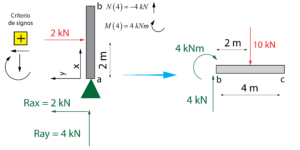
Leyes de esfuerzo en la viga b-c
A continuación obtenemos las leyes de esfuerzo en la viga b-c, teniendo en cuenta las nuevas cargas y momento flector que han sido transferidas al extremo b de la viga. De nuevo, como hay una carga puntual aplicada a la distancia de 2 metros, tendremos dos tramos distintos en la viga. Al ser un elemento horizontal, los ejes x e y se encuentran en la dirección habitual.
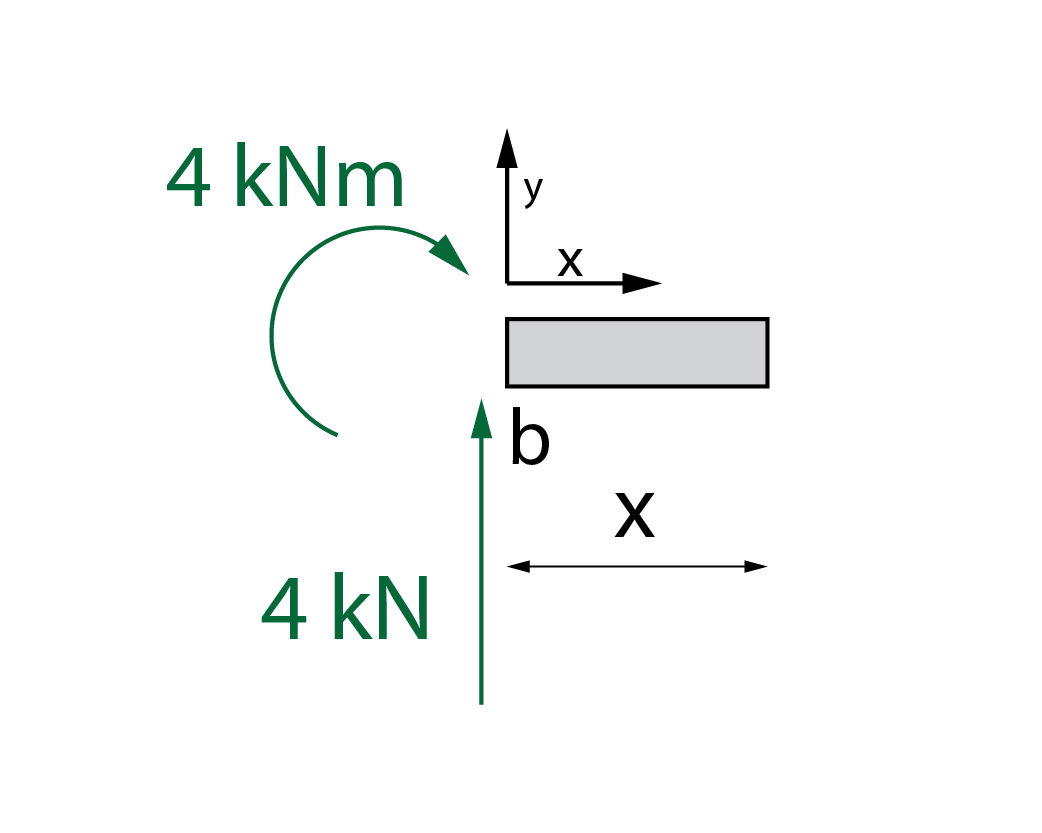
\begin{array}{l}\left. {N\left( x \right)} \right|_0^2 = 0\;kN\\\\\left. {V\left( x \right)} \right|_0^2 = 4\;kN\\\\\left. {M\left( x \right)} \right|_0^2 = 4 + 4x\;kNm\end{array}
\begin{array}{l}\left. {N\left( x \right)} \right|_2^4 = 0\;kN\\\\\left. {V\left( x \right)} \right|_2^4 = 4 – 10 = – 6\;kN\\\\\left. {M\left( x \right)} \right|_2^4 = 4 + 4x – 10\left( {x – 2} \right) = – 6x + 24\;kNm\end{array}
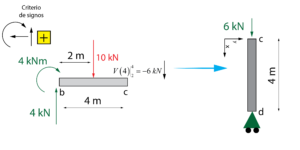
Sustituyendo x = 4 m, que es la posición del extremo c de la viga, se calculan los esfuerzos que se transferirán al último pilar.
\begin{array}{l}\left. {N\left( 4 \right)} \right|_2^4 = 0\;kN\\\\\left. {V\left( 4 \right)} \right|_2^4 = – 6\;kN\\\\\left. {M\left( 4 \right)} \right|_2^4 = – 6 \cdot 4 + 24 = 0\;kNm\end{array}
Estos esfuerzos deben son transferidos al pilar c-d teniendo en cuenta las siguientes consideraciones:
- El esfuerzo axial es nulo en el extremo c de la viga, por lo que no se transfieren cargas de cortante al pilar.
- El cortante en el extremo final de la viga es negativo. Siguiendo el criterio de signos para los esfuerzos, esto es sentido «hacia abajo», lo que se transfiere como una fuerza vertical al pilar. Es decir, el cortante de la viga se transfiere como esfuerzo axial al pilar, al estar estos girados 90º respectivamente.
- No hay momento flector en el extremo final de la viga, por lo que no se transfieren momentos al pilar.
Leyes de esfuerzo en el pilar c-d
Con las cargas transferidas de la viga al extremo inicial del pilar, se calculan los esfuerzos en el mismo. Se debe tener en cuenta los ejes locales del pilar, girados 90º a partir del extremo d. Esto es, el eje x queda en dirección longitudinal del pilar (en dirección c-d), mientras que el eje y es perpendicular a la dirección del pilar.
Únicamente hay un tramo en el pilar, al no existir cargas intermedias. Sólo hay esfuerzo axial N=-6\,kN, ya que solo hay una carga aplicada en dirección del eje longitudinal, siendo un esfuerzo de compresión. No existe cortante ni momento flector.
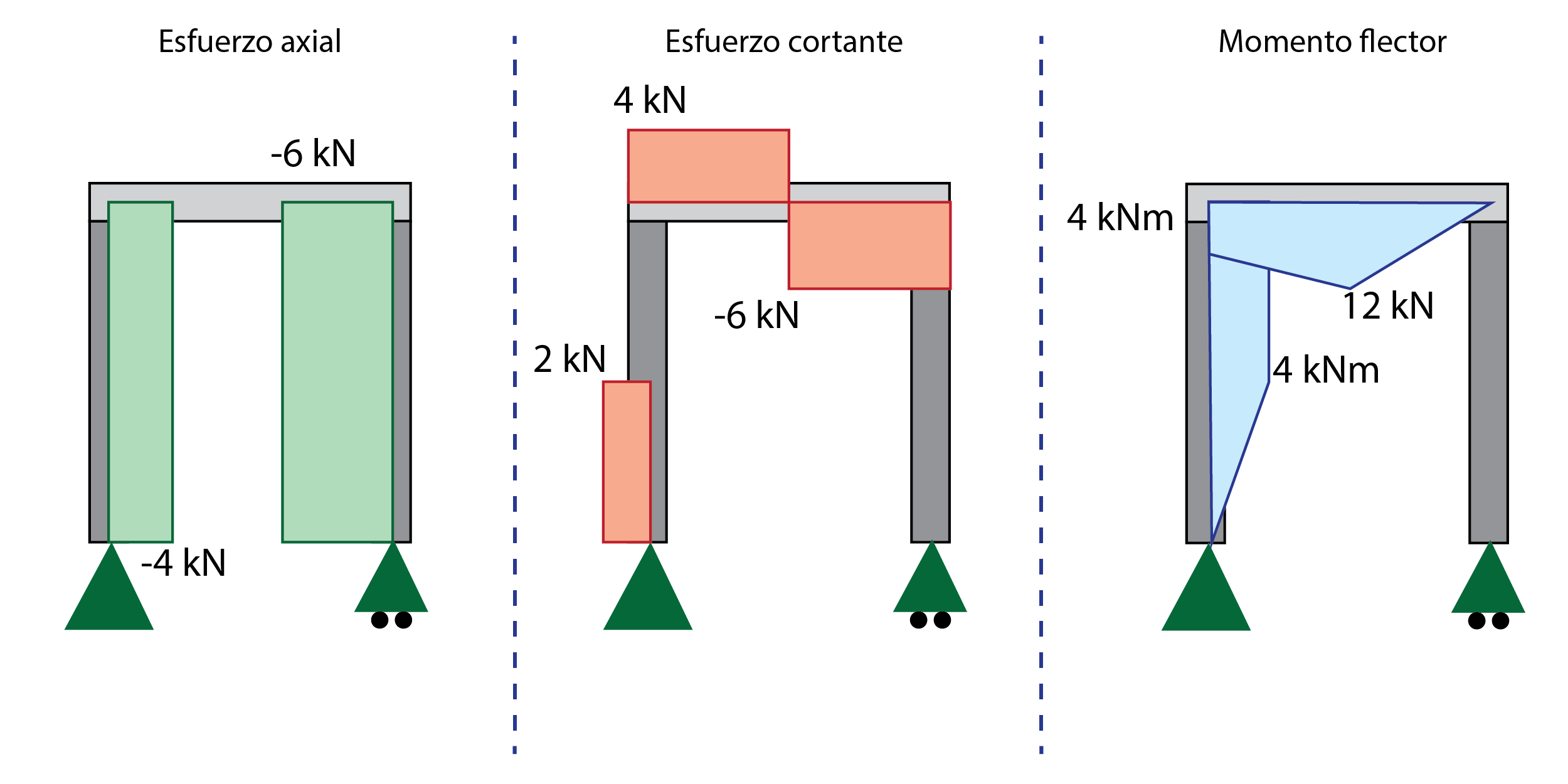
6. Representación de los diagramas de esfuerzo
Con las leyes de esfuerzo calculadas, ya es posible representar los diagramas de esfuerzo. Realmente, este paso es similar al caso de vigas individuales. Únicamente hay que tener en cuenta que los pilares están girados para representar el signo de los esfuerzos correctamente.
Si queréis ampliar un poco más vuestros conocimientos sobre la resolución y cálculo de pórticos os animo a ver este vídeo donde hay más ejemplos resueltos!!