Los trenes de engranajes epicicloidales o planetarios son muy importantes en la construcción de mecanismos. En este artículo explicamos como realizar el análisis cinemático de trenes epicicloidales, resolviendo algún ejemplo. Además, al final del artículo tenéis un vídeo con animaciones y más información. También podéis ojear el artículo previo sobre trenes de engranajes fijos.
1. Módulo de un engranaje
Para que dos ruedas dentadas puedan formar un engranaje, es decir, engranen con precisión transmitiéndose el movimiento de una a otra, deben tener el mismo módulo. El módulo, m, es una relación geométrica entre el diámetro primitivo, d, de la rueda y su número de dientes, z.
m = \dfrac{d}{z}
Para un módulo dado, mayor será el diámetro de la rueda cuanto mayor sea el número de dientes.
De manera muy simplificada, el módulo indica cuánto de espaciados están los dientes en el engranaje. Si dos ruedas tienen distinto módulo no podrán formar un engranaje porque los dientes chocarán de manera defectuosa al producirse el giro.

2. Velocidad en el punto de contacto
Con el objetivo de simplificar la redacción del artículo, a partir de ahora se hará uso de la palabra «engranaje» para referirnos a cualquier rueda o piñón (algo que es muy común).
Cuando se analiza una pareja de engranajes, la velocidad lineal, V, en el punto de contacto entre ambos (dos engranajes únicamente contactan en un diente) debe ser la misma. La velocidad para el engranaje A, V_A, puede calcularse a partir de la velocidad de giro (velocidad angular), \omega_A, del engranaje, multiplicada por su radio, r_A.
{V_A} = {\omega _A} \cdot {r_A}
De manera análoga, la velocidad lineal en el punto de contacto para el engranaje B, V_B, se obtiene como
{V_B} = {\omega _B} \cdot {r_B}
Como se ha comentado, ambas velocidades son iguales, por lo que
{V_A} = {\omega _A} \cdot {r_A} = {\omega _B} \cdot {r_B} = {V_B}
El radio de los engranajes puede expresarse como la mitad del diámetro, que puede sustituirse por el módulo y el número de dientes, resultando
{\omega _A} \cdot \dfrac{{{d_A}}}{2} = {\omega _B} \cdot \dfrac{{{d_B}}}{2}
{\omega _A} \cdot \dfrac{{{m_A} \cdot {z_A}}}{2} = {\omega _B} \cdot \dfrac{{{m_B} \cdot {z_B}}}{2}
Como el módulo de A y B debe ser el mismo, se puede simplificar a ambos lados de la ecuación, obteniendo finalmente
{\omega _A} \cdot {z_A} = {\omega _B} \cdot {z_B}
Es decir, la velocidad de rotación de los engranajes queda definida por el número de dientes de cada uno. Conocida la velocidad de giro del engranaje A, la velocidad de giro de B se obtiene a partir de la relación entre el número de dientes de ambos engranajes
{\omega _B} = \pm {\omega _A} \cdot \dfrac{{{z_A}}}{{{z_B}}}
Obsérvese que se ha añadido el símbolo \pm a la igualdad. Esto tiene que ver con el sentido de giro del engranaje conducido (en este caso B) con respecto al sentido de giro del engranaje conductor (A). Si se trata de engranajes exteriores, B girará en sentido contrario, debiendo escoger el sentido negativo (-). En cambio, si se trata de un par interior (uno de los engranajes es más pequeño que el otro y gira en el interior, piñón y corona), ambos tendrán el mismo sentido de giro, tomando el sentido positivo (+).
Nota: la elección del sentido positivo o negativo no responde a un criterio general, únicamente a la relación entre ambos engranajes.
Si el tren de engranajes tiene un número mayor de elementos, la velocidad de salida del tren, \omega_s, se obtiene, a partir de la velocidad de entrada, \omega_e, multiplicando el número de dientes de los engranajes conductores y dividiendo entre los conducidos. Esto se encuentra más detallado en el siguiente enlace.
{\omega _s} = \pm {\omega _e} \cdot \dfrac{{\prod {{z_{conductores}}} }}{{\prod {{z_{conducidos}}} }}
3. Trenes de engranajes epicicloidales
Los trenes de engranajes epicicloidales se diferencian de los trenes de engranajes fijos en que al menos uno de los engranajes cambia su posición durante el movimiento. Es decir, además de girar, mueve su posición guiado por otro elemento llamado brazo.
Para resolver este tipo de trenes hay que incluir una actualización a la fórmula anterior, añadiendo el término relativo a la velocidad de giro del brazo, \omega_b
\dfrac{{{\omega _s} – {\omega _b}}}{{{\omega _e} – {\omega _b}}} = \pm \dfrac{{\prod {{z_{conductores}}} }}{{\prod {{z_{conducidos}}} }}
Esta ecuación es conocida como Fórmula de Willis.
Nota: la elección del signo siempre quedará definida por el sentido de giro relativo (igual o contrario) de ambos engranajes.
4. Ejercicio
Obtener la velocidad y sentido de giro del engranaje 4 y del brazo sabiendo que el engranaje 2 gira a 900 rpm en sentido horario y que el engranaje 5 está fijo (bloqueado).

Se observa que se trata de un tren planetario donde el eslabón 3 corresponde con el brazo. Este gira el movimiento del engranaje 4, que se desplaza mientras gira alrededor del engranaje 2. Para poder obtener las velocidades del brazo y del engranaje 4 debemos aplicar la ecuación de Willis. Sin embargo, primero es necesario conocer los sentidos de giro para poder utilizar la correctamente.
El análisis de sentidos de giro debe completarse imaginando que se trata de un tren de engranajes fijos, es decir, ninguno de desplaza de su posición. Aunque se trate de una situación irreal, permite seleccionar el signo positivo o negativo en la aplicación de la fórmula. El resultado posterior del cálculo indicará el sentido de giro real:
- El engranaje 2 gira en sentido horario, el cual tomaremos como sentido positivo (+).
- Si se tratara de un tren de ejes fijos, como los engranajes 2 y 4 son exteriores, el sentido de giro del engranaje 4 sería contrario al engranaje 2. Por lo tanto, giraría en sentido antihorario, que es negativo (-).
- Finalmente, si el tren fuera de ejes fijos, como los engranajes 4 y 5 son interiores, 5 giraría en el mismo sentido que 4. Es decir, giraría en sentido antihorario negativo (-).
Ahora ya estamos preparados para aplicar la fórmula de Willis. Esta fórmula tiene 3 variables, las velocidades de salida y entrada y la velocidad del brazo, por lo que se necesita conocer al menos dos para poder aplicarla. En este caso, sabemos la velocidad de entrada del engranaje 2, \omega_2=900\,rpm, y conocemos la velocidad de salida del engranaje 5. Como es un engranaje bloqueado, \omega_5=0\,rpm.
De este modo, utilizando el signo (-), como ambos engranajes girarían en sentidos contrarios en un hipotético tren fijo, obtenemos la velocidad del brazo, \omega_b, multiplicando por los engranajes conductores (2 y 4) y dividiendo por los conducidos (4 y 5) como
\dfrac{{0 – {\omega _b}}}{{900 – {\omega _b}}} = – \dfrac{{24 \cdot 40}}{{40 \cdot 104}}
Despejando, se obtiene {\omega _b} = 168,75\;rpm. Es decir, el brazo gira en sentido horario, que es el positivo.
Conociendo esta variable, podemos volver a aplicar la ecuación, tomando como entrada la velocidad del engranaje 2 y salida la velocidad del engranaje 4. En este caso, como girarían en sentidos contrarios en el hipotético tren fijo, se aplica la ecuación con el signo (-). El engranaje 2 es conductor y el engranaje 4 es conducido.
\dfrac{{{\omega _4} – 168,75}}{{900 – 168,75}} = – \dfrac{{24}}{{40}}
Obtenemos {\omega _4} = – 270\;rpm. Es decir, el engranaje 4 gira en sentido antihorario.
5. Trenes de engranajes compuestos
También hay trenes de engranajes compuestos de trenes fijos y trenes epicicloidales, como el mostrado en la figura siguiente. Estos ejercicios se calculan aplicando los fundamentos anteriores, utilizando la ecuación de Willis únicamente en la parte planetaria. Este ejercicio propuesto se encuentra resuelto en el vídeo del final del artículo.
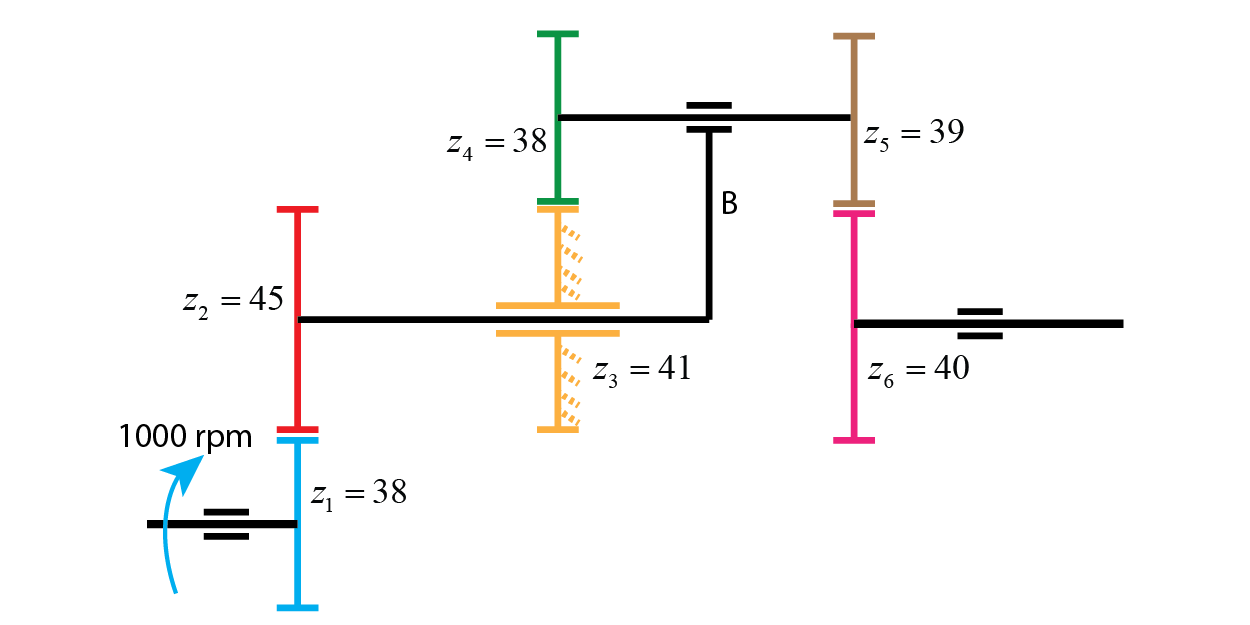
Si queréis ampliar un poco más vuestros conocimientos sobre trenes de engranajes os animo a ver el siguiente vídeo donde se muestran más ejemplos!!
