El cálculo de vigas consiste en la determinación de los esfuerzos y deformaciones generadas en las vigas como resultado de las cargas aplicadas y supone la base del cálculo estructural. En general, aunque en casos muy específicos las vigas puedan estar sometidas a torsión, serán los esfuerzos de axil, cortante y momento flector los que normalmente aparezcan. Mediante los procedimientos de la resistencia de materiales seremos capaces de determinar la magnitud de estos esfuerzos en todos los puntos de la viga, describiendo las leyes de esfuerzos.
En este artículo establecemos los principios básicos para calcular y resolver vigas isostáticas, planteando y resolviendo algún caso sencillo. Además, en el vídeo del final hay disponible más ejemplos resueltos.
Índice de apartados del artículo
Introducción al cálculo de vigas
Cargas aplicadas y reacciones
En primer lugar, es importante distinguir entre qué son las cargas aplicadas y qué son las reacciones generadas como resultado de estas cargas. Una carga es toda aquella fuerza o momento que se aplica sobre la viga, como el peso de la nieve, su propio peso o el empuje del viento.
Las fuerzas pueden ser puntuales (aplicadas en un sólo punto), o distribuidas sobre una longitud de la viga (bien de manera constante o siguiendo alguna función o geometría). Por su parte, los momentos de giro se aplican siempre en una sección concreta de al viga.
Para mantener el equilibrio estático en la viga, es necesario que se produzcan reacciones. La viga no está aislada, estará sujeta en otros elementos (vigas, pilares, suelo, pared…) que generarán, como resultado de las cargas aplicadas, una reacción sobre la viga en forma de fuerzas o momentos.

El estado tensional de la viga, y por lo tanto, las deformaciones, serán resultado conjunto de las cargas aplicadas y las reacciones presentes.
De lo anterior se deduce que el valor de las reacciones es influido por la magnitud de las cargas aplicadas. Sin embargo, las reacciones también dependen de las restricciones presentes en la viga. Lógicamente, no es lo mismo que una viga se deje simplemente apoyada por sus extremos, o que un extremo se introduzca completamente en una pared, empotrándolo. Las limitaciones de movimiento que estos distintos apoyos introducen en la viga definen sus restricciones.
Tipos de apoyos y restricciones
Cuando resolvemos una viga para obtener sus tensiones y deformaciones, realmente se está calculando un modelo matemático que intenta reproducir las condiciones reales de la viga. Esto implica utilizar un sistema de apoyos que simule aquellas restricciones de movimiento que pueden encontrarse en la realidad (apoyar sobre una superficie, empotrar completamente un extremos, fijar una posición…).
De manera general (aunque pueden darse más variantes), para el cálculo de vigas podemos identificar tres tipos de apoyos:
1. Apoyo deslizante (deslizadera): este apoyo restringe el desplazamiento en la dirección perpendicular al apoyo, permitiendo el desplazamiento en la otra dirección. Como resultado, aparecerá una reacción en la dirección cuyo desplazamiento está restringido.
2. Apoyo fijo: este apoyo restringe cualquier tipo de desplazamiento, aunque sí está permitido el giro. Como resultado, aparecerán dos reacciones, una horizontal y otra vertical.
3. Apoyo empotrado (empotramiento): este apoyo restringe tanto los desplazamiento como el giro, generando tres reacciones, las dos fuerzas más un momento de giro.
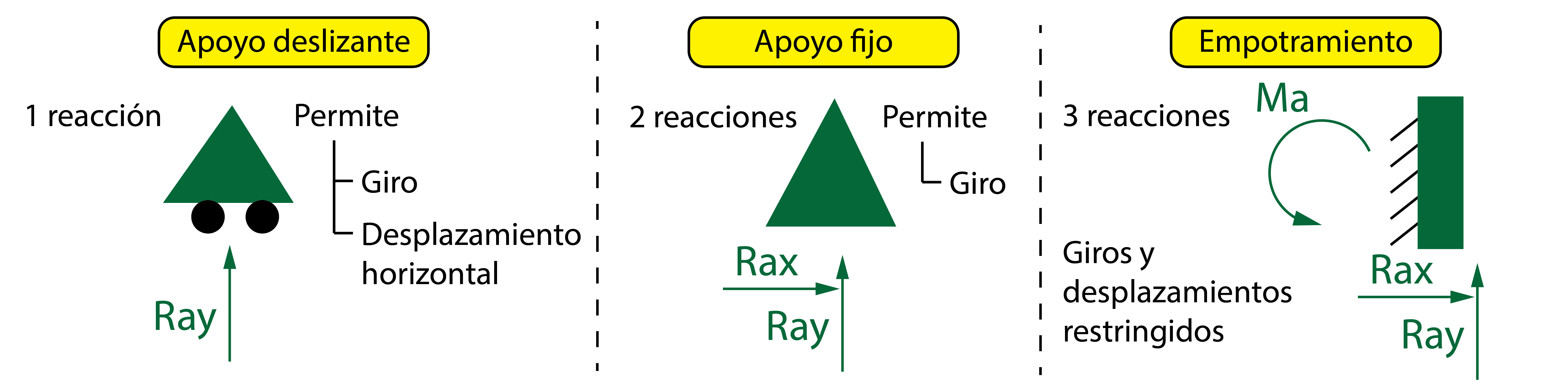
Una viga real será entonces modelizada para su cálculo matemático a partir de las cargas aplicadas y una combinación de apoyos situados en distintas secciones de la viga. Los apoyos definirán el número de reacciones en la viga, que son las incógnitas que debemos obtener para resolverla.
¿Qué es una viga isostática?
El último concepto importante antes de comenzar a resolver vigas isostáticas es entender qué significa este concepto. Una viga será isostática si es posible realizar su análisis estático aplicando las ecuaciones de sumatorio de fuerzas y momentos.
Si se trata de un análisis en el plano (el más común) se disponen de tres ecuaciones, dos relativas al sumatorio de fuerzas horizontales y verticales, y una tercera relativa al sumatorio de momentos de giro. Por lo tanto, para resolver el sistema de ecuaciones, el número total de reacciones (incógnitas) en la viga debe ser 3, coincidente con el número de ecuaciones estáticas disponibles.
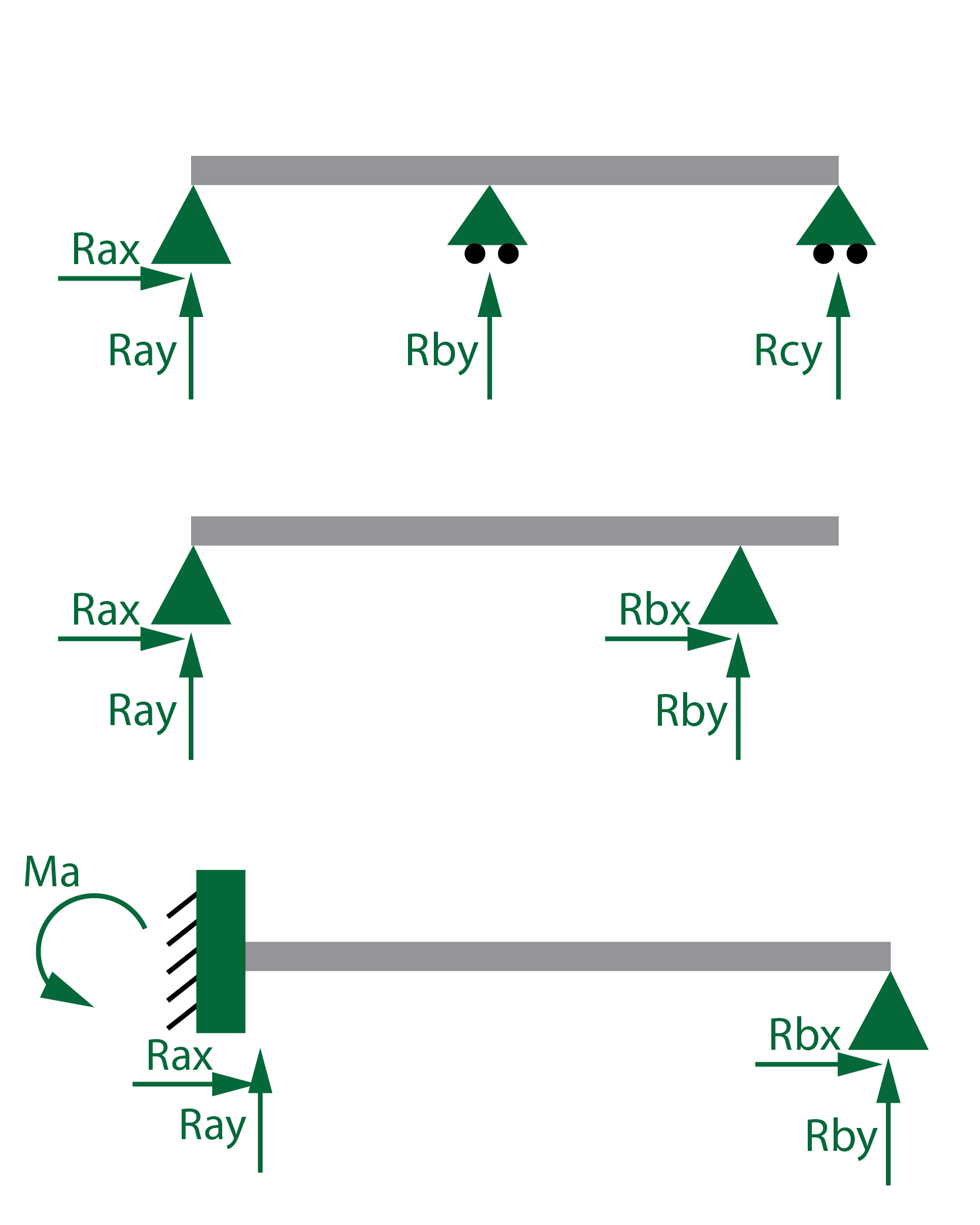
Si el número de reacciones es inferior, la viga será un mecanismo y si el número de reacciones es superior a 3, se tratará de una viga hiperestática. El grado de hiperestaticidad será mayor conforme aumente el número de reacciones redundantes. Este tipo de vigas no puede calcularse directamente, debiendo utilizar pasos adicionales para su resolución.
Las vigas isostáticas se pueden resolver fácilmente ya que el número de reacciones incógnita es igual al número de ecuaciones estáticas disponibles.
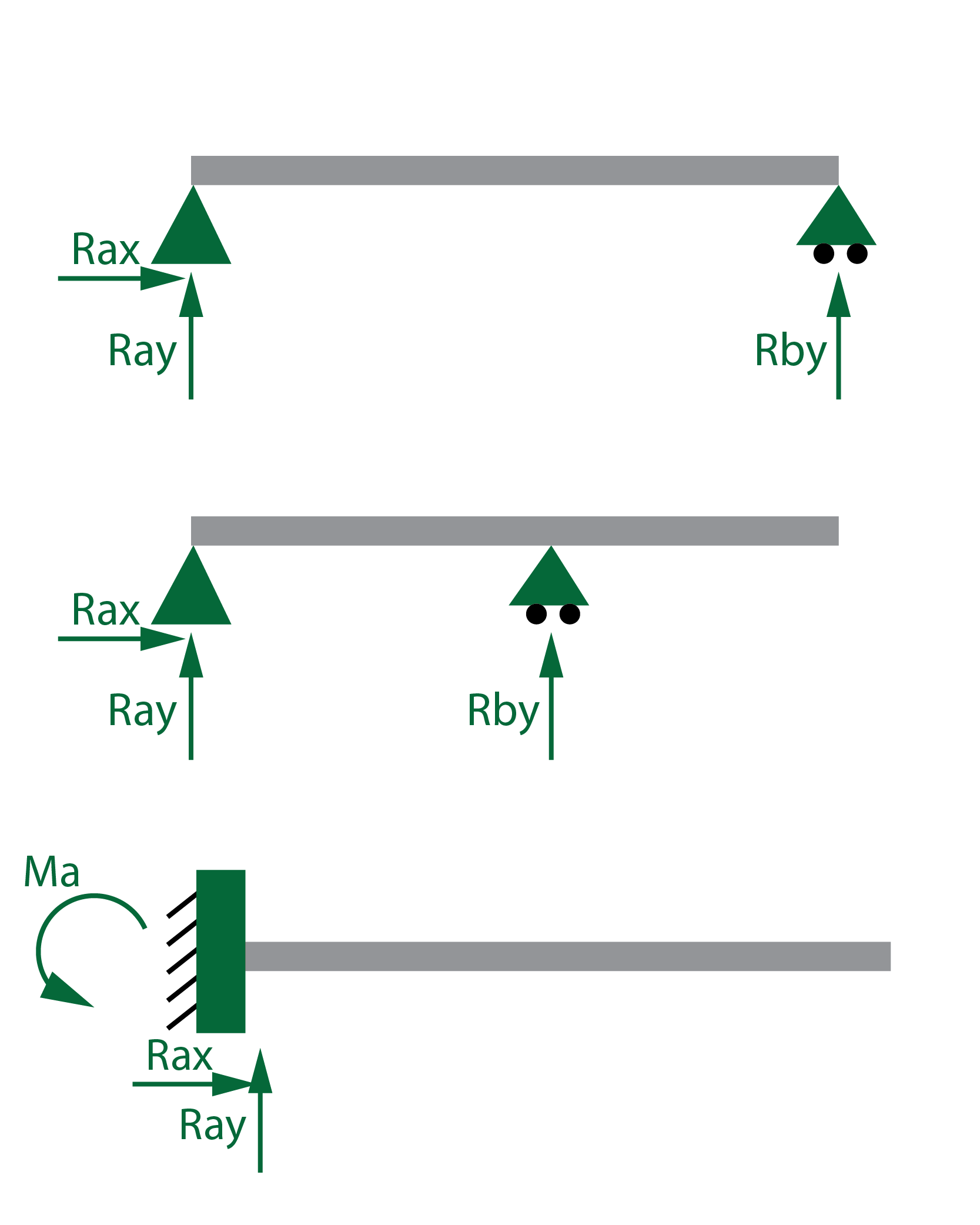
El número de reacciones incógnita de las vigas hiperestáticas es superior al número de ecuaciones estáticas disponibles.
Tipos de esfuerzos en una viga
Las cargas y reacciones producen los siguientes esfuerzos en una viga (ignorando la torsión que rara vez ocurre):
- Esfuerzo axil: genera tensiones normales, según la dirección del eje longitudinal de la viga. Es producido por la suma de todas las cargas y reacciones paralelas al eje longitudinal de la viga.
- Esfuerzo cortante: genera tensiones tangenciales en la viga. Es producido por aquellas cargas y reacciones aplicadas en dirección perpendicular al eje longitudinal de la viga.
- Momento flector: normalmente es el esfuerzo más determinante y genera tensiones normales en la viga. Es producida por aquellas cargas y reacciones perpendiculares al eje longitudinal de la viga, fuerzas paralelas al eje pero descentradas y momentos de giro aplicados.
¿Cómo se calculan las reacciones, leyes de esfuerzo y diagramas de una viga?
Una vez que se han expuesto los conceptos básicos y principios del cálculo de vigas, comenzamos con la explicación del método de resolución de vigas isostáticas simples. El proceso cuenta de las etapas siguientes:
1. Determinación de las reacciones.
2. Obtención de las leyes de esfuerzo axil, cortante y momento flector en todos los tramos de la viga.
3. Representación de los diagramas de esfuerzo.
A continuación, cada una de estas etapas se explica en detalle, aplicadas a la resolución del siguiente caso práctico.
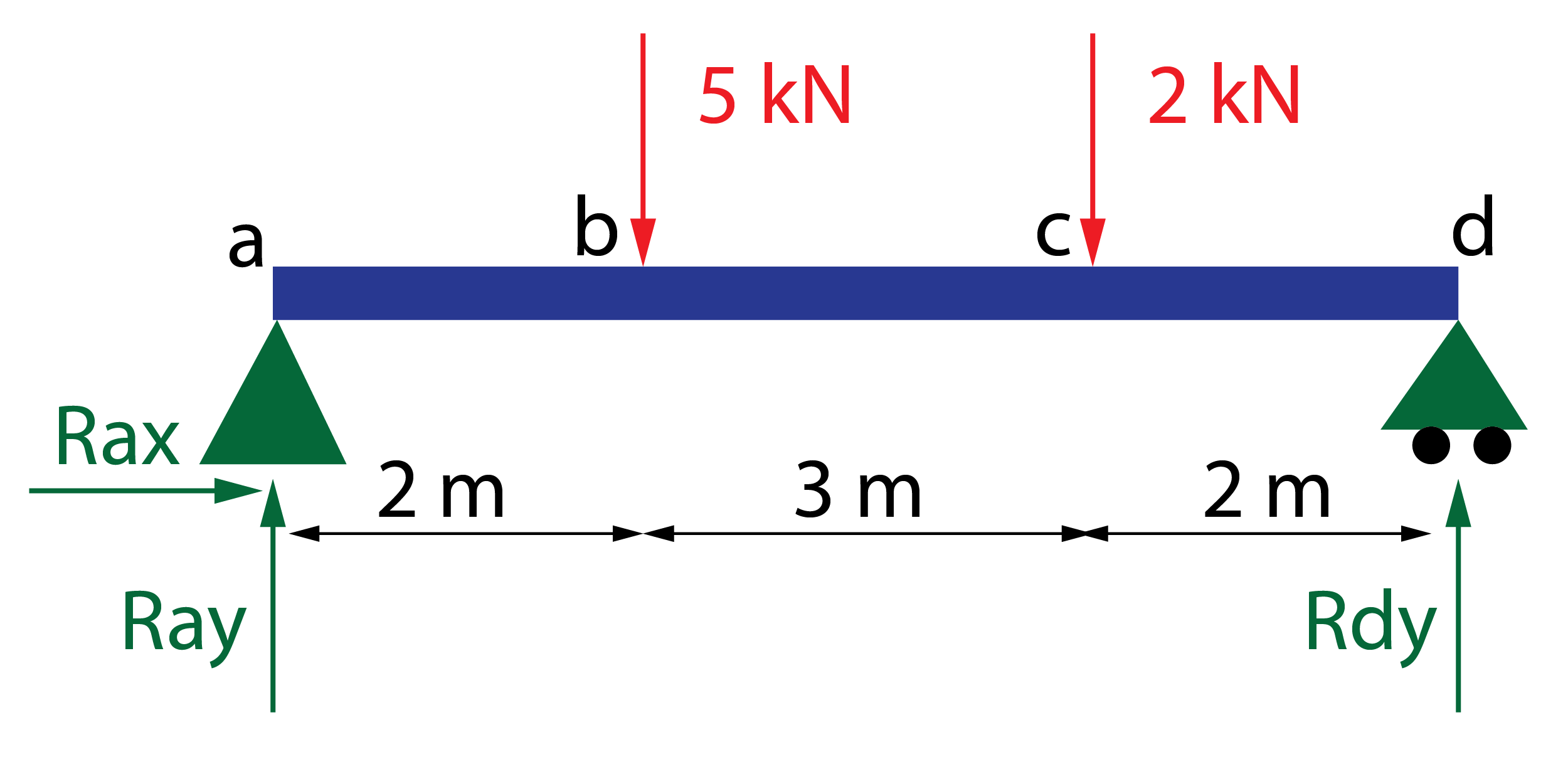
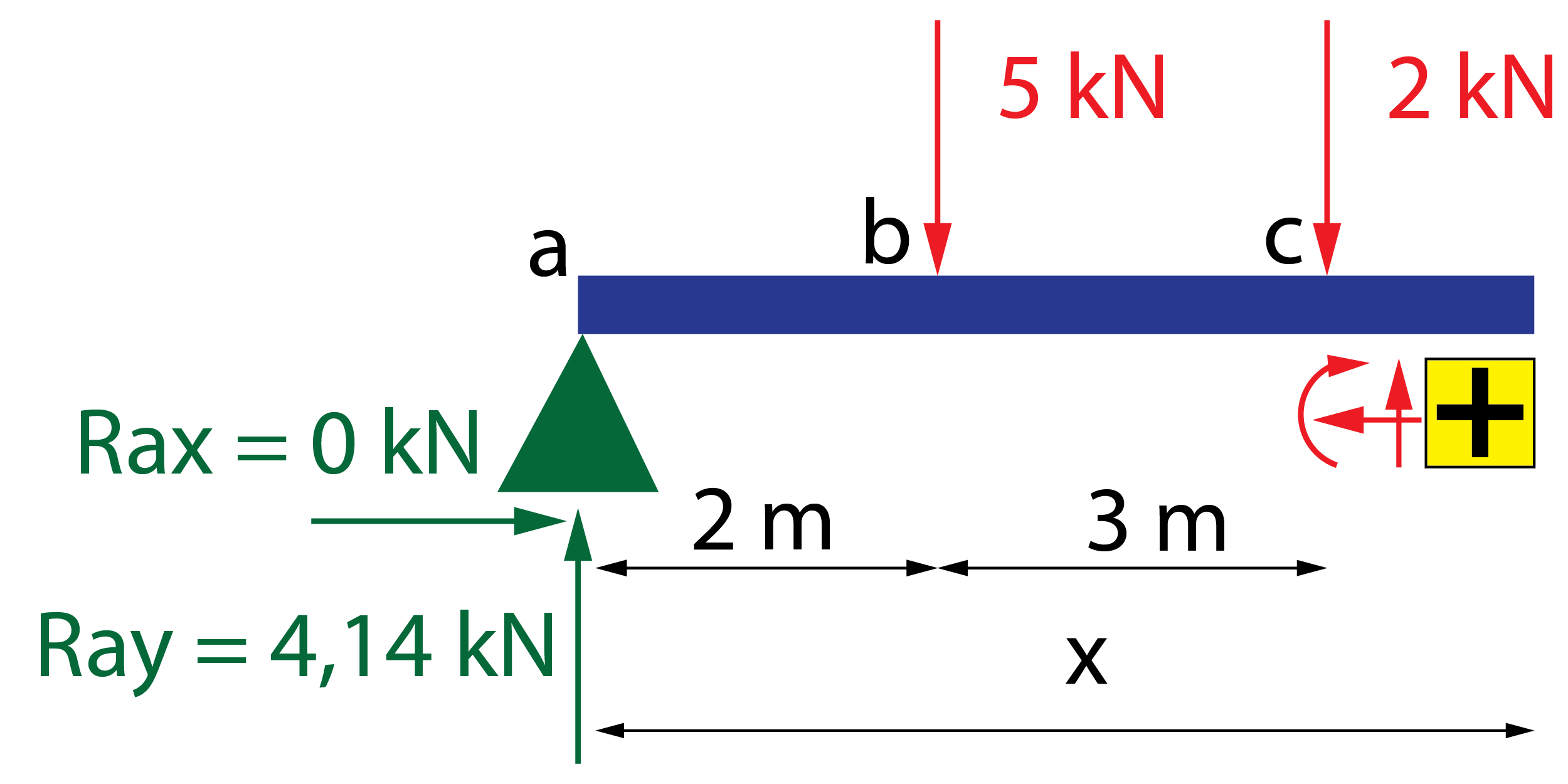
Calcular las reacciones, determinar las leyes de esfuerzos y representar los diagramas de esfuerzos para la siguiente viga isostática.
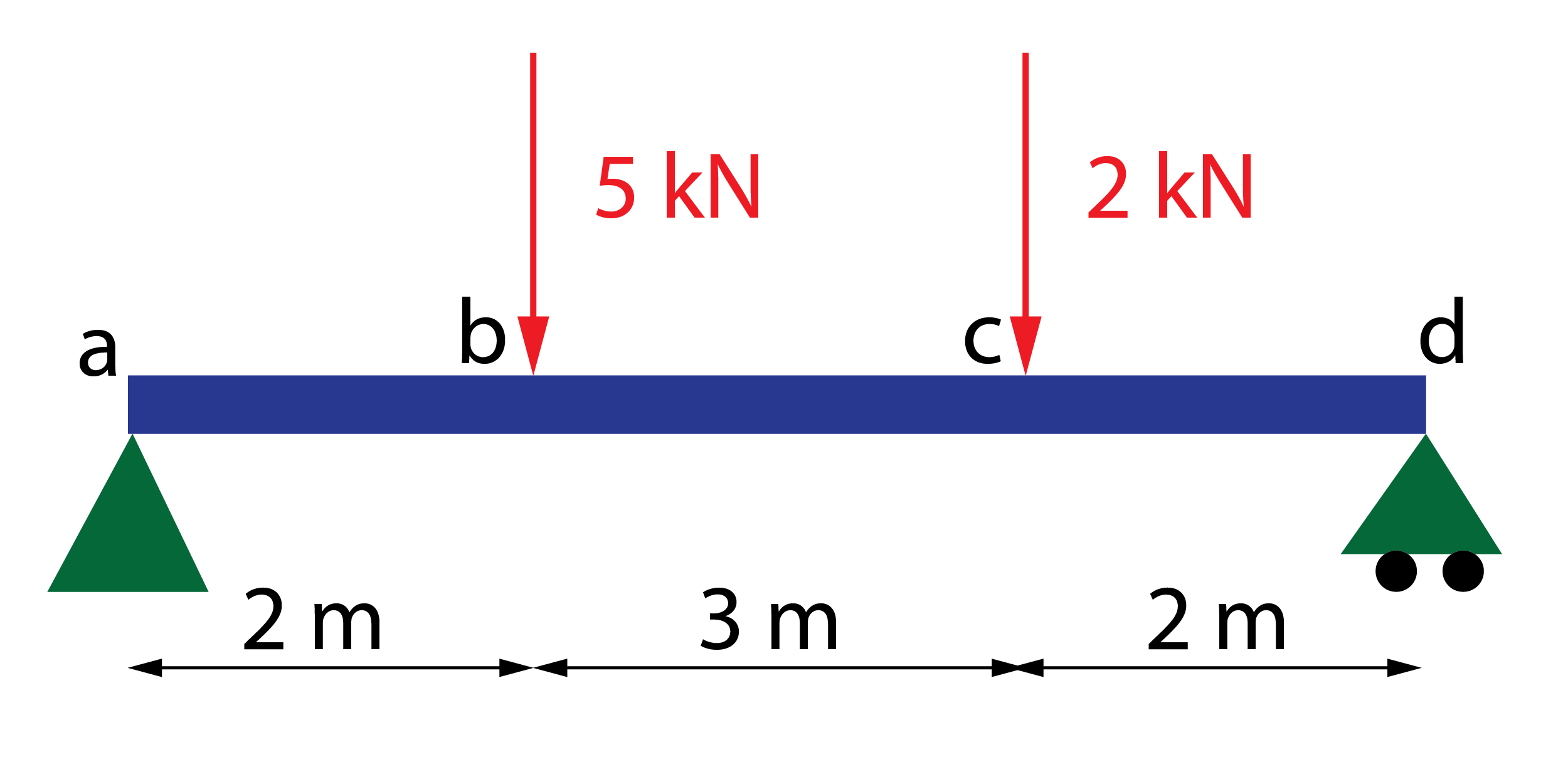
1. Determinación de las reacciones de una viga isostática
El primer paso consiste en obtener el valor de las reacciones que los apoyos definidos en la viga generan como respuesta a las cargas aplicadas.
El apoyo a es un apoyo fijo, por lo que genera dos reacciones, una fuerza en dirección horizontal, Rax, y otra fuerza en dirección vertical, Ray. El apoyo d es un apoyo deslizante. Tal y como está colocado, permite el desplazamiento en la dirección horizontal, por lo que restringe la dirección vertical, generando la fuerza Rdy. Inicialmente, el sentido de las reacciones es desconocido. Por criterio, las reacciones verticales se dibujan hacia arriba y las horizontales hacia la derecha. Si tras el cálculo, el valor es positivo, el sentido es coincidente con el planteado. Si es negativo, el sentido es contrario.
Como en total hay 3 reacciones, lo que coincide con el número de ecuaciones estáticas en el plano, la viga es isostática y puede resolverse mediante el procedimiento habitual.
Se plantean tres ecuaciones estáticas:
- Sumatorio de fuerzas horizontales: por criterio, las fuerzas aplicadas en dirección «hacia la derecha» son positivas y las aplicadas «hacia la izquierda» son negativas. La suma de todas las fuerzas debe ser igual a cero. En este caso, únicamente la reacción Rax es horizontal, por lo que su valor es cero.
\sum {{F_x} = 0 \to Rax = 0\, kN}
- Sumatorio de fuerzas verticales: por criterio, las fuerzas aplicadas «hacia arriba» serán positivas, y las aplicadas «hacia abajo» serán negativas. La suma total de las fuerzas deber ser igual a cero. En este caso, las dos reacciones Ray y Rdy son positivas y las dos fuerzas negativas.
\sum {{F_y} = 0 \to Ray + Rdy – 5 – 2 = 0}
- Sumatorio de momentos en una sección: elegiremos una sección de la viga para realizar el equilibrio de momentos. Es recomendable seleccionar aquella que más incógnitas elimine, en este caso, la sección a, ya que hay dos fuerzas aplicadas en este punto que no generan momento. En el planteamiento de esta ecuación necesitamos hacer uso de la distancia desde el punto de aplicación de las fuerzas hasta a. Para entender cómo plantear la ecuación, pensaremos en una palanca que gira respecto de la sección a, desde el punto de aplicación de cada fuerza. Si el giro es «antihorario» el signo será positivo. Si es «horario» se tomará como negativo. En este caso, la reacción Rdy genera un momento positivo, multiplicada por la distancia total desde d hasta a (7 m). La fuerza de 5 kN, genera un momento negativo (distancia 2 m), y la fuerza de 2 kN genera un momento negativo (distancia 5 m).
\sum {{M_a} = 0 \to 7 \cdot Rdy – 2 \cdot 5 – 5 \cdot 2 = 0}
Despejando en la tercera ecuación, se obtiene Rdy=2,86 \,kN. Sustituyendo en la segunda ecuación, se calcula Ray=4,14 \,kN.
\sum {{F_x} = 0 \to Rax = 0\, kN}
\sum {{F_y} = 0 \to Ray + Rdy – 5 – 2 = 0}
\sum {{M_a} = 0 \to 7 \cdot Rdy – 2 \cdot 5 – 5 \cdot 2 = 0}
2. Obtención de las leyes de esfuerzo axil, cortante y momento flector en todos los tramos de la viga
Una vez que los valores de las reacciones en los apoyos de la viga son conocidas, es posible obtener las leyes de esfuerzo en cada tramo de la viga.
Una ley de esfuerzo es una función que representa el esfuerzo axil, cortante o momento flector en todas las secciones de la viga, desde un extremo a otro en función de la posición. Para ello, definiremos distancia x como la longitud desde el extremo izquierdo de la viga hasta la sección de evaluación.
El procedimiento consiste en partir la viga en tramos, separados por cambios de carga o apoyos. Es decir, recorriendo la viga de derecha a izquierda, se definirá un tramo cuando aparezca una nueva carga o un apoyo.
Siguiendo este criterio, esta viga se divide en tres tramos, a-b, b-c y c-d, definidos por la aplicación de las cargas puntuales.
Por lo tanto, x representará la distancia desde a hasta una sección de corte en el tramo a-b, lo que servirá para obtener las leyes en este tramo.
Seguidamente, x representará la distancia desde a hasta una sección de corte en el tramo b-c, lo que servirá para obtener las leyes en este tramo.
Por último, x representará la distancia desde a hasta una sección de corte en el tramo b-c, lo que servirá para obtener las leyes el tramo final.

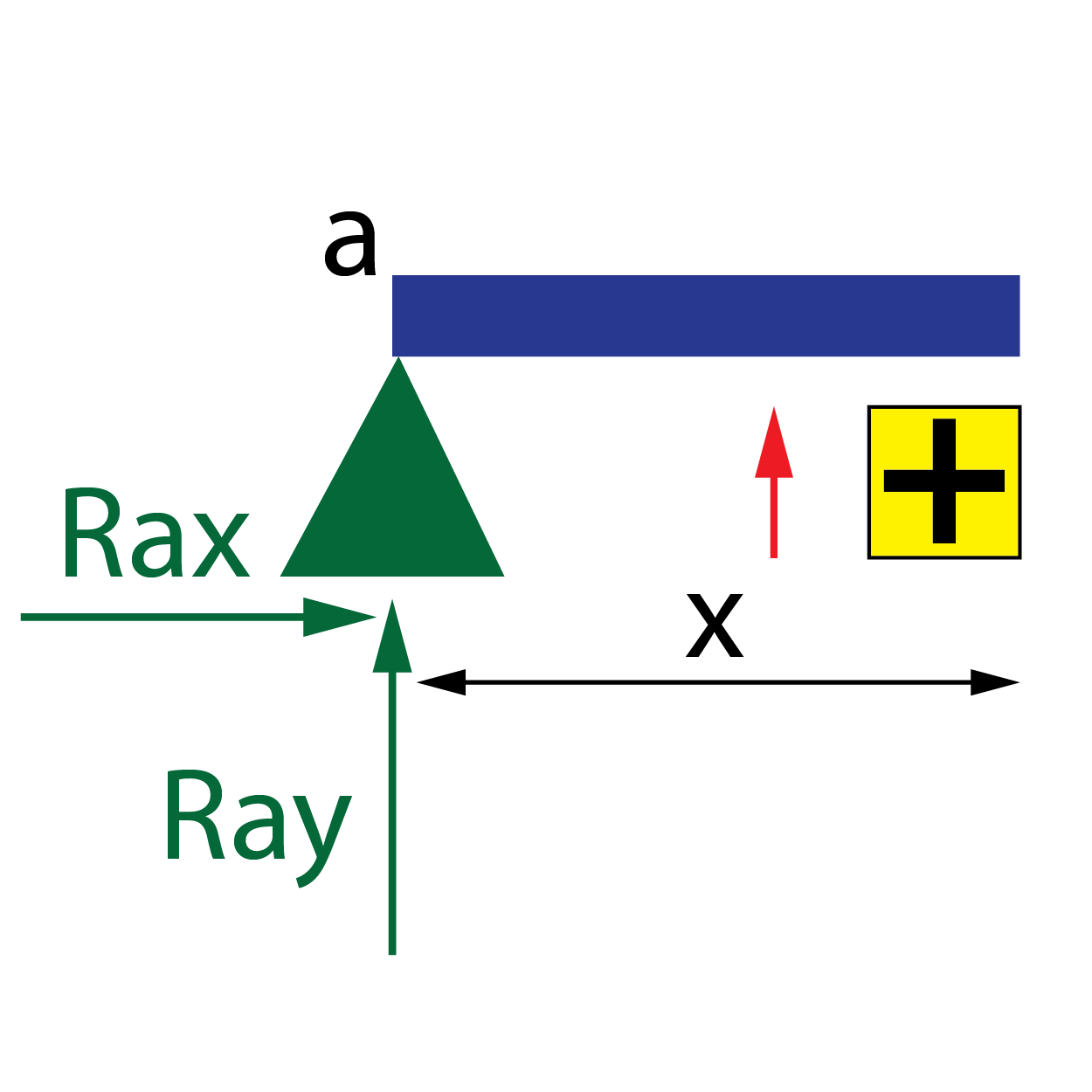
Antes de analizar cada tramo y obtener las leyes de esfuerzo, es necesario definir un criterio de signos.
- Esfuerzo axil, N: se toma como criterio positivo el esfuerzo de tracción, es decir, aquellas cargas que tienen a incrementar la longitud de la barra. Por lo tanto, la compresión es negativa. A nivel del procedimiento de análisis se traduce en definir como criterio positivo todas aquellas fuerzas en dirección paralela al eje de la viga que, situadas a la izquierda de la sección x, están dirigidas hacia la izquierda.

- Esfuerzo cortante, V: aquellas fuerzas situadas a la izquierda de la sección x con dirección perpendicular al eje de la viga y hacia arriba generarán un cortante positivo.
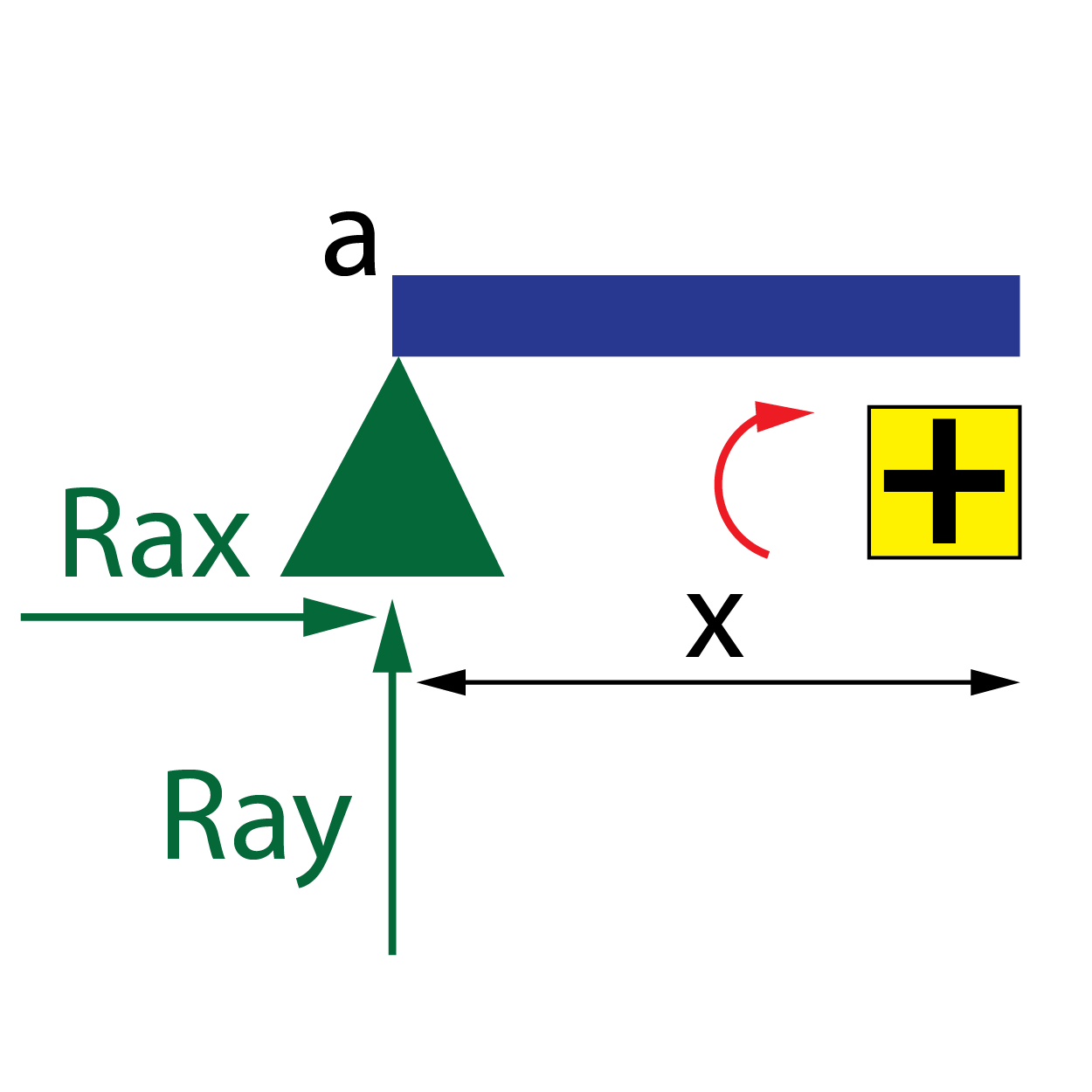
- Momento flector, M: se tomará como criterio de momento positivo, el sentido horario producido por las cargas situadas a la izquierda de la sección x.
A partir de estos criterios establecidos, podemos obtener las leyes de esfuerzos en cada uno de los tramos.
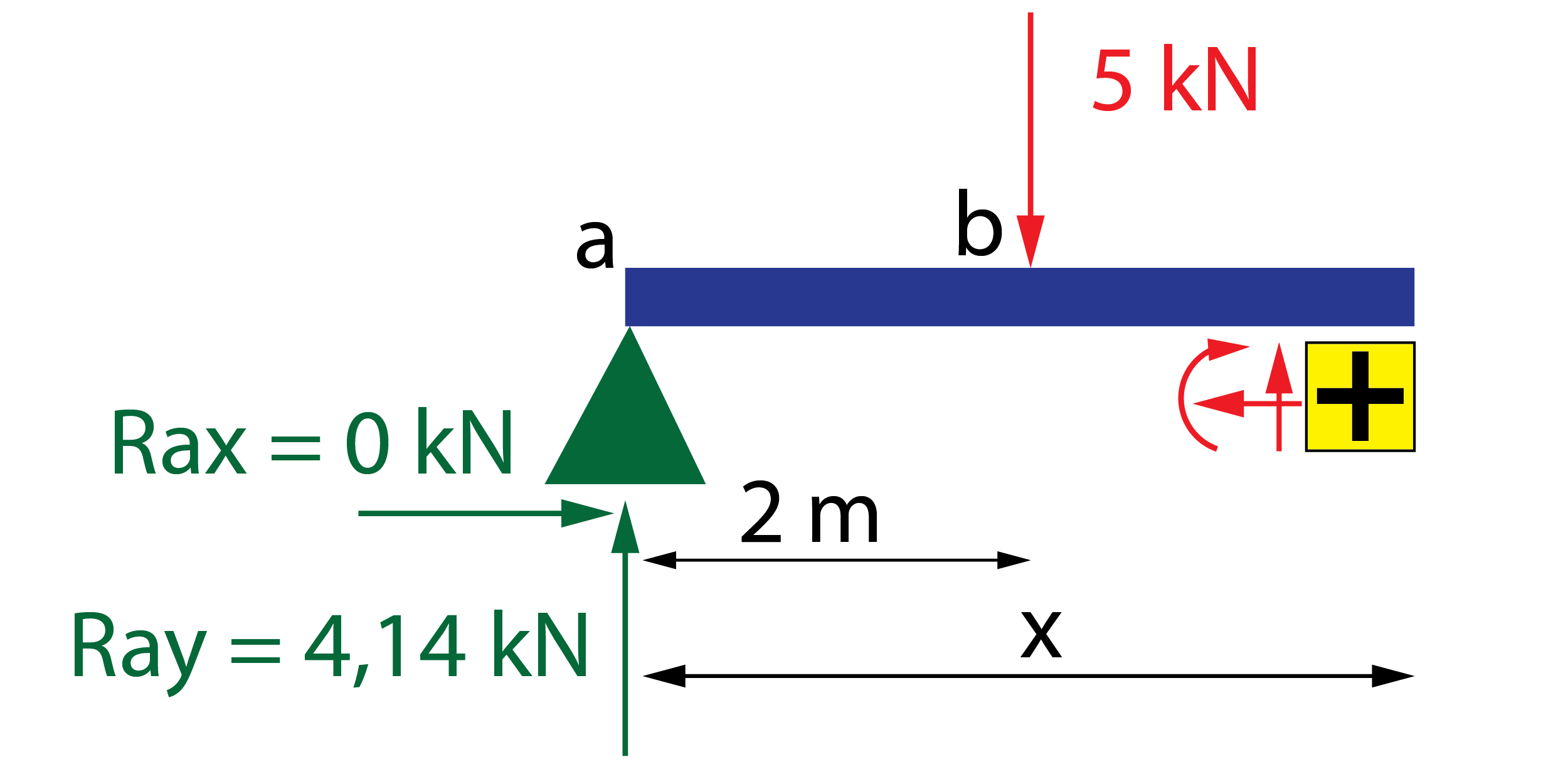
Tramo a-b

El esfuerzo axil es nulo, ya que no hay fuerzas en dirección paralela al eje de la viga.
\left. {N\left( x \right)} \right|_a^b = Rax = 0
La componente vertical Ray de la reacción en el apoyo a es la única fuerza en dirección perpendicular a la viga que genera cortante.
\left. {V\left( x \right)} \right|_a^b = Ray = 4,14\;kN
El momento flector es generado por la reacción Ray, cuya distancia a la sección x es la distancia x. Genera un momento en sentido positivo.
\left. {M\left( x \right)} \right|_a^b = Ray \cdot x = 4,14x\;kNm
Tramo b-c
El esfuerzo axil es nulo, ya que no hay fuerzas en dirección paralela al eje de la viga.
\left. {N\left( x \right)} \right|_b^c = Rax = 0
Al cortante generado por la reacción Ray, se le añade la fuerza aplicada de 5 kN, que genera un cortante negativo.
\left. {V\left( x \right)} \right|_b^c = Ray – 5 = 4,14 – 5 = – 0,86\;kN
Al momento flector generado por la reacción Ray se suma el producido por la fuerza aplicada de 5 kN, cuya distancia a la sección analizada es (x-2). Esta fuerza genera un momento en sentido negativo.
\left. {M\left( x \right)} \right|_b^c = Ray \cdot x – 5 \cdot \left( {x – 2} \right) = – 0,86x + 10\;kNm
Tramo c-d
El esfuerzo axil es nulo, ya que no hay fuerzas en dirección paralela al eje de la viga.
\left. {N\left( x \right)} \right|_c^d = Rax = 0
Al cortante del tramo anterior hay que añadir la fuerza aplicada de 2 kN, que genera cortante en sentido negativo.
\left. {V\left( x \right)} \right|_c^d = Ray – 5 – 2 = 4,14 – 5 – 2 = – 2,86\;kN
Al momento flector del tramo anterior hay que sumar el generado por la fuerza de 2 kN, cuya distancia a la sección analizada es (x-5) y que genera un momento flector negativo.
\left. {M\left( x \right)} \right|_c^d = Ray \cdot x – 5 \cdot \left( {x – 2} \right) – 2 \cdot \left( {x – 5} \right)
= – 2,86x + 20\;kNm
3. Representación de los diagramas de esfuerzo
El último paso para acabar un ejercicio de este tipo es representar los diagramas para los tres esfuerzos. Este paso es muy sencillo, únicamente consiste en graficar las funciones que hemos obtenido en el apartado anterior para cada esfuerzo en función de la posición x de la viga.
Si observamos las leyes obtenidas, cuando las cargas aplicadas en la viga son cargas puntuales, la ley de cortante es constante en cada tramo. Por su parte, la ley de momentos es lineal, por lo que es fácilmente graficable a partir de dos valores en cada tramo.
Como única consideración importante, hay que destacar que, por cuestiones de criterio, la ley de momentos se representa invertida. Esto es, el eje de ordenadas (eje y) tiene sentido contrario, por lo que los valores positivos se representan debajo del eje, y los negativos por encima.

- Se observa como el esfuerzo axil es nulo en toda la viga, al no existir cargas aplicadas en dirección paralela al eje longitudinal de la viga.
- El esfuerzo cortante es constante en cada tramo de la viga. Para comprobar que las leyes de esfuerzo son correctas y que el diagrama está bien dibujado podemos fijarnos en el valor en los extremos de la viga, justo en los apoyos. El cortante debe ser igual a la reacción Ray y tener signo contrario a la reacción Rdy.
- El diagrama de momento flector está formado por tres rectas, una en cada tramo. Si está bien obtenido, debe cumplirse que el momento es cero en los apoyos de la viga, al tratarse de un apoyo fijo y otro deslizante que permiten el giro.
- Además, existe una relación directa entre la ley de cortante y de momento flector. La ley de cortante es la derivada del momento flector.
¿Y qué ocurre cuando las cargas no son puntuales? Cuando las cargas son distribuidas, hay que tener en cuenta el centro de gravedad de la carga. Si quieres aprender cómo analizar vigas isostáticas con cargas distribuidas y ampliar lo aprendido en este artículo, aquí tienes este vídeo!!!
