El coeficiente de Poisson es una propiedad mecánica de los materiales. Una constante elástica que define la relación entre las deformaciones en las distintas direcciones. En este artículo explicamos cómo se define y qué utilidad tiene. Además, al final del artículo tenéis un vídeo con animaciones y más información.
1. Deformación longitudinal y deformación transversal
Una barra sometida a un esfuerzo de tracción incrementa su longitud en la dirección del esfuerzo. Esto se conoce como deformación longitudinal, \epsilon_x. Análogamente, si se produce un esfuerzo de compresión, la longitud de la barra se acorta.
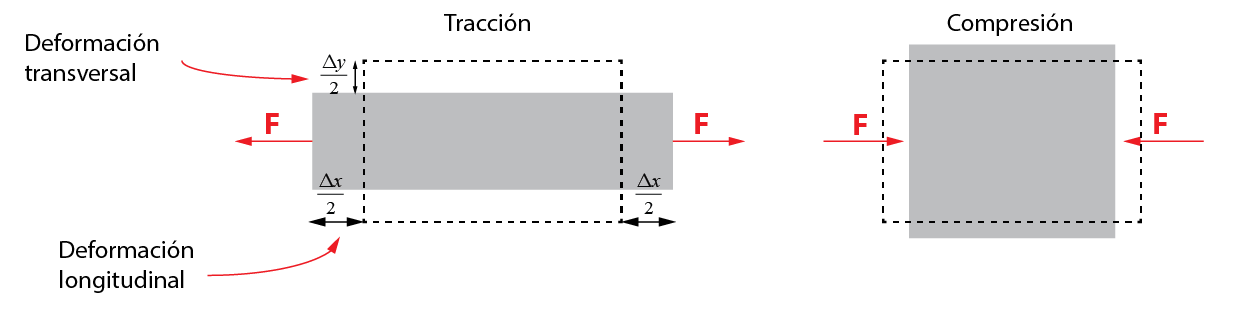
La deformación se define como la variación de longitud en una dirección, dividida entre la longitud inicial, resultando un número adimensional. La deformación longitudinal será positiva para el esfuerzo de tracción (aumento de longitud) y negativa en el caso de la compresión (menor longitud).
\epsilon_x= \dfrac{\Delta L_x}{L_x}
Sin embargo, aunque el esfuerzo se produzca en una única dirección, también se generan deformaciones en las direcciones perpendiculares del espacio, conocidas como deformaciones transversales, \epsilon_y y \epsilon_z.
A partir de la definición de deformación anterior, estas serán calculadas como
\epsilon_y= \dfrac{\Delta L_y}{L_y}, \,\, \epsilon_z= \dfrac{\Delta L_z}{L_z}
En los materiales isótropos, que son aquellos que tienen las mismas propiedades mecánicas en todas las direcciones del espacio, se cumple que las deformaciones transversales (o deformaciones laterales) son iguales.
\epsilon_y=\epsilon_z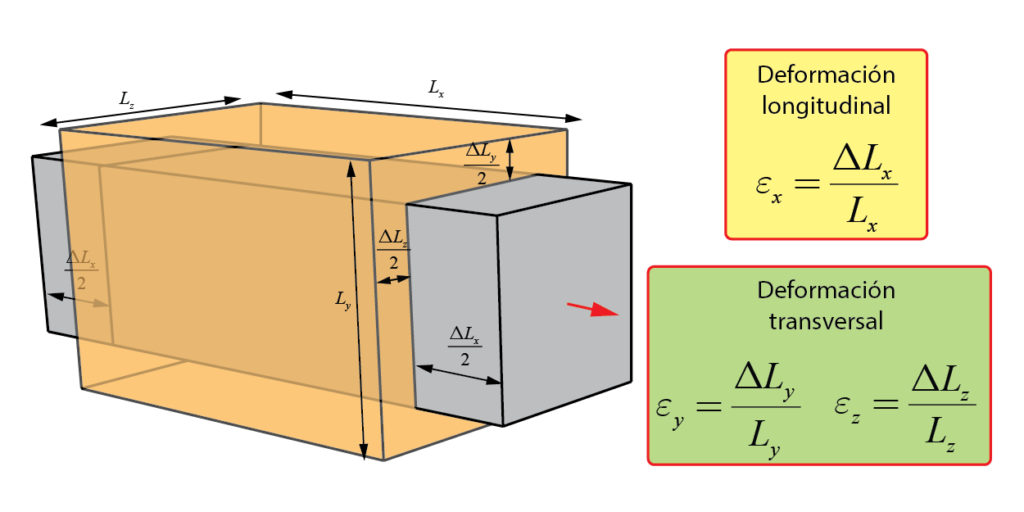
2. ¿Qué es el coeficiente de Poisson?
Las deformaciones transversales, \epsilon_y y \epsilon_z, están ligadas con la deformación longitudinal, \epsilon_x, mediante una relación constante definida por el Coeficiente de Poisson, \nu. Este se obtiene dividiendo la deformación transversal entre la deformación longitudinal.
\nu=-\dfrac{\epsilon_{transversal}}{\epsilon_{longitudinal}}=-\dfrac{\epsilon_y}{\epsilon_x}=-\dfrac{\epsilon_z}{\epsilon_x}
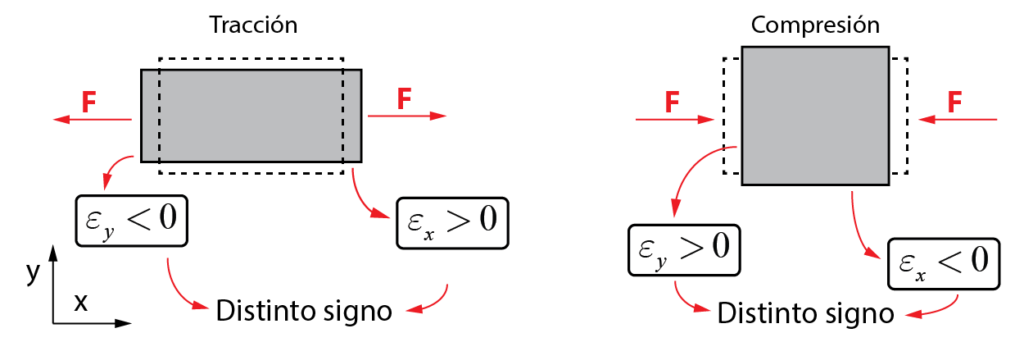
El signo negativo en la fórmula explica el efecto que intuitivamente imaginamos. Cuando la barra es traccionada (deformación longitudinal positiva), la deformación transversal debe ser negativa, ya que la barra reduce su sección. Contrariamente, para el caso de una compresión (deformación longitudinal negativa), la deformación transversal es positiva, ya que esta se ensancha.
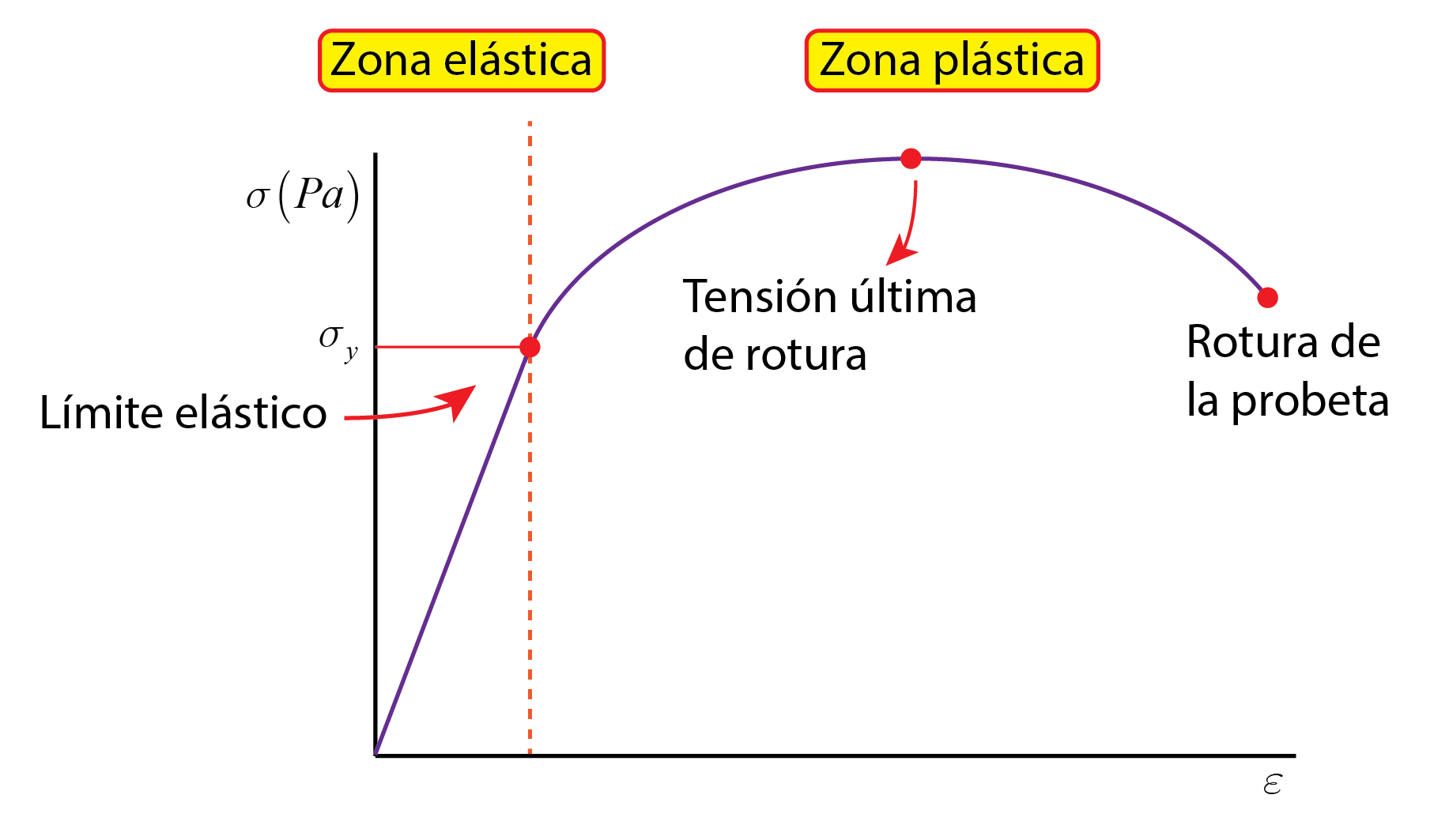
El coeficiente de Poisson es una constante elástica. Explica la relación entre las deformaciones en la zona elástica del material, donde la deformación es reversible al no superar la tensión del límite elástico. En la zona plástica de la curva tracción-deformación el estudio de las deformaciones es mucho más complejo.
3. ¿Qué valores puede tomar el coeficiente de Poisson?
Puede deducirse matemáticamente que el coeficiente de Poisson adquiere valores entre -1 y 0,5, siendo el rango entre 0 y 0,5 el más habitual:
- La mayoría de los metales tiene un coeficiente de Poisson alrededor de 0,3. Esto indica que las deformaciones transversales son aproximadamente 1/3 de la deformación longitudinal.
- Existen materiales como el corcho, con un coeficiente de Poisson \nu=0, lo que indica que no sufren deformación transversal.
- Los materiales con el máximo coeficiente, \nu=0,5, son materiales incompresibles. Su volumen no varía durante la deformación. Un ejemplo es la goma.
- Por último, los materiales auxéticos o augéticos tienen un coeficiente de Poisson negativo, como algunas espumas o polímeros. Son materiales capaces de expandirse o contraerse en todas las direcciones simultáneamente. No son muy comunes.

4. Cómo utilizar el coeficiente de Poisson
El coeficiente de Poisson es muy útil a la hora de calcular deformaciones y relacionarla con las tensiones en el material, en la zona elástica.
El caso más sencillo ocurre bajo la aplicación de una tensión uniaxial, como en el ensayo de tracción. La deformación longitudinal se calcular dividiendo la tensión en el material, \sigma_x entre su módulo elástico, E, lo que se conoce como Ley de Hooke. Recordad que la tensión es la fuerza aplicada dividida entre el área de la sección transversal, \sigma_x=\frac{F}{A}.
\epsilon_x=\dfrac{\sigma_x}{E}
A partir del coeficiente de Poisson, las deformaciones transversales se deducen como
\epsilon_y=\epsilon_z=-\nu\cdot\epsilon_x
Nótese como, aunque no hay tensiones transversales, \sigma_y y \sigma_z, sí hay deformación transversal.
En la mayoría de casos, existirán cargas en distintas direcciones, lo que somete al material a estados tridimensionales de tensión. Es decir, habrá tensiones en más de una dirección. En estos casos, se aplicarán las Leyes de Hooke generalizadas, obteniendo la deformación en cada dirección a partir de la tensión aplicada en dicha dirección y las tensiones en las otras dos, multiplicadas por el coeficiente de Poisson.
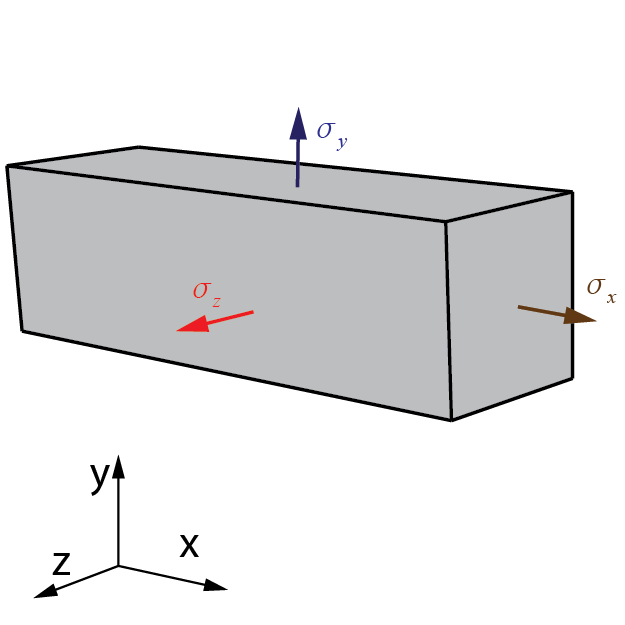
\begin{array}{l}{\varepsilon _x} = \dfrac{1}{E}\left[ {{\sigma _x} – \nu \left( {{\sigma _y} + {\sigma _z}} \right)} \right]\\\\{\varepsilon _y} = \dfrac{1}{E}\left[ {{\sigma _y} – \nu \left( {{\sigma _x} + {\sigma _z}} \right)} \right]\\\\{\varepsilon _z} = \dfrac{1}{E}\left[ {{\sigma _z} – \nu \left( {{\sigma _x} + {\sigma _y}} \right)} \right] \end{array}
Si queréis ampliar un poco más vuestros conocimientos sobre el coeficiente de Poisson os animo a ver el siguiente vídeo donde se muestran más ejemplos!!
