El movimiento en el plano de una cuerda vibrante con extremos fijos en los puntos (0, 0) y (L, 0) (con L > 0) se modela con el siguiente problema de Cauchy (donde la variable t representa el tiempo y c es una constante):
\left\{ {\begin{array}{lll} {{u_{tt}} – c^2{u_{xx}} = 0}&{0 < x < L,\;t > 0,} \\ {u(x,0) = f(x)}&{0 < x < L,} \,&\text{\small forma inicial de la cuerda}\\u_t(x,0)=g(x)&0<x<L&\text{\small velocidad inicial de la cuerda}\\ {u(0,t) = 0}&{t > 0,} \,&\\ {u(L,t) = 0}&{t > 0,}\,& \end{array}} \right.\;
Donde c es una constante.
Vamos a aplicar el método de separación de variables para buscar una solución.
Consideramos una solución de la forma u(x,t)=X(x)\cdot T(t) lo que nos lleva a
X(x)T''(t) – {c^2}X''(x)T(t) = 0
y separando variables
\dfrac{X''(x)}{X(x)}=\dfrac{T''(t)}{c^2T(t)}=\lambda.
\left\{ {\begin{array}{c} {T''(t) – {c^2}\lambda T(t) = 0} \\ {X''(x) – \lambda X(x) = 0} \end{array}} \right.
De la condición inicial u(0,t)=0, X(0)T(t)=0,\,\forall t, luego obtenemos X(0)=0. De forma análoga concluimos que X(L)=0.
Nos planteamos entonces hallar las soluciones del problema
\left\{ {\begin{array}{l} {X''(x)- \lambda X(x) = 0} \\ {X(0) = 0} \\ {X(L) = 0} \end{array}} \right.
Buscamos los valores de \lambda para los que existe solución distinta de la solución trivial X(x)=0. Estos valores se llaman valores propios y las soluciones asociadas funciones propias.
En este caso el polinomio característico es r^2-\lambda=0 cuyas soluciones son r=\pm\sqrt{\lambda}.
- \lambda=0: en este caso X(x)=a+bx, luego
\left\{ \begin{array}{l} X(0) = 0 \Rightarrow a = 0\\ X(L) = 0 \Rightarrow b L= 0 \Rightarrow b=0, \end{array} \right.
con lo que X(x)=0.
- \lambda>0: entonces X(x)=a e^{-\sqrt \lambda x}+b e^{\sqrt \lambda x}.
\left\{ {\begin{array}{l} {X(0) = 0 \Rightarrow a + b = 0} \\ {X(L) = 0 \Rightarrow a{e^{ – \sqrt \lambda L }} + b{e^{\sqrt \lambda L }} = 0} \\ \end{array} } \right.
multiplicando la segunda ecuación por e^{\sqrt \lambda L } tenemos
\left\{ {\begin{array}{l} {a + b = 0} \\ {a + b{e^{2\sqrt \lambda L}} = 0} \\ \end{array} } \right.
y restando b\left(e^{2\sqrt \lambda L }-1\right)=0, luego b=a=0 y X(x)=0.
- \lambda<0: entonces las soluciones son r=\pm\sqrt{-\lambda}i que conlleva la función
X(x)=a\cos\sqrt{-\lambda}x+b\operatorname{sen}\sqrt{-\lambda}x.
X(0) = 0 \Rightarrow a = 0 \Rightarrow X(x) = b\operatorname{sen} \sqrt { – \lambda } x
\begin{gathered} X(L) = 0 \Rightarrow b\operatorname{sen} \sqrt { – \lambda } L = 0 \Rightarrow \operatorname{sen} \sqrt { – \lambda } L = 0 \\ \sqrt { – \lambda } L = n\pi \Rightarrow \lambda = – {\left( {\dfrac{{n\pi }}{L}} \right)^2} .\\ \end{gathered}
Tenemos como valores propios
\lambda_n = – {\left( {\dfrac{{n\pi }}{L}}\right)^2}\;n=1,2,\ldots
y funciones propias
X_n(x)=A_n\operatorname{sen}\left({\dfrac{{n\pi }}{L}}x\right).
Para estos valores propios debemos ahora resolver
{T''(t) + {c^2}{\left( {\dfrac{{n\pi }}{L}} \right)^2} T(t) = 0}
que tiene como ecuación característica r^2+{c^2}{\left( {\dfrac{{n\pi }}{L}} \right)^2}=0 cuyas raíces son r=\pm c\left( \dfrac{n\pi }{L} \right)i, luego obtenemos que
{T_n}(t) = {B_n}\cos \left(\dfrac{{n\pi c}}{L}t\right) + {C_n}\operatorname{sen}\left( \dfrac{{n\pi c}}{L}t\right)
y la solución general del problema es
u(x,t) = \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos\left(\dfrac{{n\pi c}}{L}t\right) + {b_n}\operatorname{sen}\left( \dfrac{{n\pi c}}{L}t\right)} \right)} \operatorname{sen} \left({\dfrac{{n\pi }}{L}}x\right)
Para determinar los coeficientes , de la condición u(x,0)=f(x) tenemos
f(x) = \sum\limits_{n = 1}^\infty {{a_n}\operatorname{sen} \left({\dfrac{{n\pi }}{L}}x\right)}
y por lo tanto a_n son los coeficientes de Fourier del desarrollo en senos de la función f(x) en el intervalo [0,L].
{a_n} = \displaystyle\dfrac{2}{L}\int_0^L {f(x)} \operatorname{sen} \left({\dfrac{{n\pi }}{L}}x\right)\,dx.
Como
{u_t}(x,t) = \sum\limits_{n = 1}^\infty \dfrac{{n\pi c}}{L}\left( – {a_n}\operatorname{sen}\left( \dfrac{{n\pi c}}{L}t\right) + {b_n}\cos \left(\dfrac{{n\pi c}}{L}t\right) \right) \operatorname{sen} \left({\dfrac{{n\pi }}{L}}x\right)
tenemos
{u_t}(x,0) = g(x) = \sum\limits_{n = 1}^\infty {\dfrac{{n\pi c}}{L}{b_n}} \operatorname{sen} \left({\dfrac{{n\pi }}{L}}x\right)
luego {\dfrac{{n\pi c}}{L}{b_n}} son los coeficientes del desarrollo de Fourier en senos de la función g(x) en el intervalo [0,L], es decir,
\displaystyle\frac{{n\pi c}}{L}{b_n} = \frac{2}{L}\int_0^L {g(x)\operatorname{sen} \left( {\frac{{n\pi }}{L}x} \right)dx} \Rightarrow {b_n} = \frac{2}{{n\pi c}}\int_0^L {g(x)\operatorname{sen} \left( {\frac{{n\pi }}{L}x} \right)dx}.
Ejemplo: Hallar la solución del problema
\left\{ {\begin{array}{ll} {{u_{tt}} – {u_{xx}} = 0} & {0 < x < \pi ,\:t > 0,} \\ {u(x,0) = 0} & {0 < x < \pi ,} \\ {{u_t}(x,0) = x(\pi – x)} & {0 < x < \pi ,} \\ {u(0,t) = 0} & {t > 0,} \\ {u(\pi ,t) = 0} & {t > 0.} \\ \end{array} } \right.
Como tenemos que c^2=1 y L=\pi, la solución es
u(x,t) = \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos nt + {b_n}\operatorname{sen} nt} \right)} \operatorname{sen}nx.
Con la condiciones iniciales a_n=0\; \forall n y
b_n=\displaystyle\frac{2}{n\pi}\int_0^\pi\left(\pi x-x^2\right)\operatorname{sen} nx\,dx.
\begin{darray}{l} {b_n} = \frac{2}{{n\pi }}\int_0^\pi {\left( {\pi x – {x^2}} \right)\operatorname{sen} nxdx} = \underbrace { – \frac{2}{{\pi {n^2}}}\left[ {\left( {\pi x – {x^2}} \right)\cos nx} \right]_0^\pi }_0 + \frac{2}{{\pi {n^2}}}\int_0^\pi {(\pi – 2x)\cos nxdx}\\ \left. {\begin{darray}{l} {u = \pi x – {x^2}} & {dv = \operatorname{sen} nxdx} \\ {du = (\pi – 2x)dx} & {v = – \frac{1}{n}\cos nx} \\ \end{darray} } \right\} \end{darray}
e integrando otra vez por partes
\begin{darray}{l} {b_n} =\frac{2}{{\pi {n^2}}}\int_0^\pi {(\pi – 2x)\cos nxdx} = \frac{2}{{\pi {n^3}}}\underbrace {\left[ {(\pi – 2x)\operatorname{sen} nx} \right]_0^\pi }_0 + \frac{4}{{\pi {n^3}}}\int_0^\pi {\operatorname{sen} nxdx}\\ \left. {\begin{array}{l} {u = \pi – 2x} & {dv = \cos nxdx} \\ {du = – 2dx} & {v = \frac{1}{n}\operatorname{sen} nx} \\ \end{array} } \right\} = – \frac{4}{{\pi {n^4}}}\left[ {\cos nx} \right]_0^\pi = – \frac{4}{{\pi {n^4}}}\left( {{{( – 1)}^n} – 1} \right)\\ \end{darray}
entonces si n es par b_n=0 y si n es impar b_n=\dfrac{8}{\pi n^4}.
Podemos escribir la solución como
\boxed{\color{blue}u(x,t) = \dfrac{8}{\pi }\sum\limits_{n = 1}^\infty {\dfrac{1}{{ {{(2n – 1)}^4}}}\operatorname{sen} (2n – 1)t\operatorname{sen} (2n – 1)x.}}
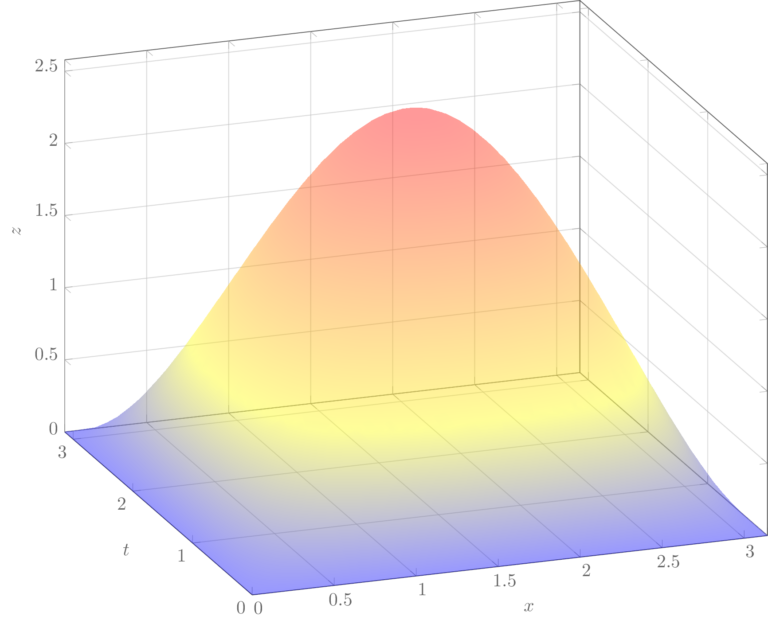
Utilizamos ahora el método de separación de variables para resolver un problema no homogéneo.
Ejemplo: Resolver el problema
\left\{ {\begin{array}{ll} {u_{tt}} -{u_{xx}}=x, &0<x<\pi,\,t>0,\\ u(x,0) = 0, &0<x<\pi,\\ u_t(x,0) = 0, &0<x<\pi, \\ u(0,t)=0, &t>0,\\ u(\pi,t)=0,&t>0. \end{array}} \right.\;
Considerando la solución como u(x,t)= X(x)\cdot T(t) y sustituyendo en la ecuación se obtiene
\dfrac{{T''(t)}}{{T(t)}} = \dfrac{{X''(x)}}{{X(x)}} \Rightarrow \left\{ {\begin{array}{c} {T''(t) – \lambda T(t) = 0} \\ {X''(x) – \lambda X(x) = 0} \end{array}} \right.
que con la condiciones de
\left\{ \begin{gathered} u(x,0) = 0 \Rightarrow X(x) \cdot T(0) = 0 \Rightarrow T(0) = 0,\\ {u_t}(x,0) = 0 \Rightarrow X(x) \cdot T'(0) = 0 \Rightarrow T'(0) = 0, \\ u(0,t) = 0 \Rightarrow X(0) \cdot T(t) = 0 \Rightarrow X(0) = 0, \\ u(\pi ,t) = 0 \Rightarrow X(\pi ) \cdot T(t) = 0 \Rightarrow X(\pi ) = 0. \\ \end{gathered} \right.
nos lleva a estudiar las soluciones de
\left\{ {\begin{array}{l} {X''(x) – \lambda X(x) = 0} \\ {X(0) = 0} \\ {X(\pi) = 0} \end{array}} \right.
y obtenemos los valores propios
\lambda_n = -n^2,\;n=1,2,\ldots
y funciones propias X_n(x)=\operatorname{sen}(nx).
Consideremos la solución
u(x,t)= \sum\limits_{n = 1}^\infty {T_n(t)\operatorname{sen}(nx)}.
aplicando la ecuación, como
u_{tt}=\sum\limits_{n = 1}^\infty {T''_n(t)\operatorname{sen}(nx)}.
u_{xx}=\sum\limits_{n = 1}^\infty -n^2{T_n(t)\operatorname{sen}(nx)}.
entonces
u_{tt}-u_{xx}= \sum\limits_{n = 1}^\infty {\left(T''_n(t)+n^2T_n(t)\right)\operatorname{sen}(nx)}=x,
por lo que T''_n(t)+n^2T_n(t) son los coeficientes del desarrollo en senos de la función x, es decir,
\begin{gathered} T''_n(t)+n^2T_n(t)= \frac{2}{\pi }\int_0^\pi {x\operatorname{sen} nxdx} = – \frac{2}{{\pi n}}\left[ {x\cos nx} \right]_0^\pi +\underbrace {\frac{2}{{\pi n}}\int_0^\pi {\cos nxdx}}_0\\ \left. {\begin{array}{l} {u = x}&{dv = \operatorname{sen} nxdx} \\ {du = dx}&{v = – \frac{1}{n}\cos nx} \end{array}} \right\}\; = – \frac{2}{{\pi n}}\left( {\pi {{( – 1)}^n}} \right) = \frac{{2{{( – 1)}^{n + 1}}}}{n}. \end{gathered}
y debemos resolver el problema
\left\{\begin{array}{l} T''_n(t)+n^2T_n(t)=\dfrac{2(-1)^{n+1}}{n}, \\ T_n(0)=0, \\ T'_n(0)=0. \end{array}\right.
Como la ecuación característica es r^2+n^2=0 con soluciones t=\pm ni, la solución de la ecuación homogénea es
T_h(t)=A\cos nt+B\operatorname{sen} nt.
Una solución particular será de la forma T_p(t)=k constante, y aplicando la condición de la ecuación, como T''_p(t)=0
T''_p(t)+n^2T_p(t)=n^2 k=\dfrac{2(-1)^{n+1}}{n}\Rightarrow k=\dfrac{2(-1)^{n+1}}{n^3}.
La solución general por lo tanto es
T_n(t)=A\cos nt+B\operatorname{sen} nt+\dfrac{2(-1)^{n+1}}{n^3}.
De T_n(0)=0 obtenemos
A+\dfrac{2(-1)^{n+1}}{n^3}=0\Rightarrow A=-\dfrac{2(-1)^{n+1}}{n^3}=\dfrac{2(-1)^{n}}{n^3}.
Como T'_n(t)=-nA\operatorname{sen} nt+nB\cos nt, si T'_n(0)=0 debe ser nB=0 y B=0. Concluimos que
T_n(t)=\dfrac{2(-1)^{n}}{n^3}\cos nt+\dfrac{2(-1)^{n+1}}{n^3}=\dfrac{2(-1)^{n}}{n^3}\left(\cos nt-1\right).
La solución del problema es
\boxed{\color{blue}u(x,t)= \sum\limits_{n = 1}^\infty{\dfrac{2(-1)^{n}}{n^3}\left(\cos nt-1\right)\operatorname{sen} nx}.}
