La ecuación unidimensional del calor es el modelo de variación de la temperatura u según la posición x y el tiempo t en una varilla calentada de longitud L y de temperatura inicial f(x) que se extiende a lo largo del eje X y cuyos extremos se mantienen a una temperatura constante de cero grados en todo instante. Se obtiene el problema de Dirichelt
\left\{ {\begin{array}{lll} {{u_t} – c^2{u_{xx}} = 0}&{0 < x < L,\;t > 0,} \\ {u(x,0) = f(x)}&{0 < x < L,} \,&\text{\small temperatura inicial}\\ {u(0,t) = 0}&{t > 0,} \,&\text{\small temperatura extremo izquierdo}\\ {u(L,t) = 0}&{t > 0,}\,&\text{\small temperatura extremo derecho} \end{array}} \right.\;
Donde c es una constante.
Vamos a aplicar el método de separación de variables para buscar una solución.
Consideramos una solución de la forma u(x,t)=X(x)\cdot T(t) lo que nos lleva a
X(x)T'(t) – {c^2}X''(x)T(t) = 0
y separando variables
\dfrac{X''(x)}{X(x)}=\dfrac{T'(t)}{c^2T(t)}=\lambda.
De la condición inicial u(0,t)=0, X(0)T(t)=0,\,\forall t, luego obtenemos X(0)=0. De forma análoga concluimos que X(L)=0.
Nos planteamos entonces hallar las soluciones del problema
\left\{ {\begin{array}{l} {X''(x)- \lambda X(x) = 0} \\ {X(0) = 0} \\ {X(L) = 0} \end{array}} \right.
Buscamos los valores de \lambda para los que existe solución distinta de la solución trivial X(x)=0. Estos valores se llaman valores propios y las soluciones asociadas funciones propias.
En este caso el polinomio característico es r^2-\lambda=0 cuyas soluciones son r=\pm\sqrt{\lambda}.
- \lambda=0: en este caso X(x)=a+bx, luego
\left\{ \begin{array}{l} X(0) = 0 \Rightarrow a = 0\\ X(L) = 0 \Rightarrow b L = 0 \Rightarrow b=0, \end{array} \right.
con lo que X(x)=0.
- \lambda>0: entonces X(x)=a e^{-\sqrt \lambda x}+b e^{\sqrt \lambda x}.
\left\{ {\begin{array}{l} {X(0) = 0 \Rightarrow a + b = 0} \\ {X(L ) = 0 \Rightarrow a{e^{ – \sqrt \lambda L}} + b{e^{\sqrt \lambda L }} = 0} \\ \end{array} } \right.
multiplicando la segunda ecuación por e^{\sqrt \lambda L } tenemos
\left\{ {\begin{array}{l} {a + b = 0} \\ {a + b{e^{2\sqrt \lambda L }} = 0} \\ \end{array} } \right.
y restando b\left(e^{2\sqrt \lambda L }-1\right)=0, luego b=a=0 y X(x)=0.
- \lambda<0: entonces las soluciones son r=\pm\sqrt{-\lambda}i que conlleva la función
X(x)=a\cos\sqrt{-\lambda}x+b\operatorname{sen}\sqrt{-\lambda}x.
X(0) = 0 \Rightarrow a = 0 \Rightarrow X(x) = b\operatorname{sen} \sqrt { – \lambda } x
\begin{gathered} X(L) = 0 \Rightarrow b\operatorname{sen} \sqrt { – \lambda } L = 0 \Rightarrow \operatorname{sen} \sqrt { – \lambda } L = 0 \\ \sqrt { – \lambda } L = n\pi \Rightarrow \lambda = – {\left( {\dfrac{{n\pi }}{L}} \right)^2} .\\ \end{gathered}
Tenemos como valores propios
\lambda_n = – {\left( {\dfrac{{n\pi }}{L}}\right)^2}\;n=1,2,\ldots
y funciones propias
X_n(x)=a_n\operatorname{sen}\left({\dfrac{{n\pi }}{L}}x\right).
Para estos valores propios debemos ahora resolver
\dfrac{T'(t)}{T(t)}=c^2\lambda_n
cuya solución es
T_n(t)=b_ne^{c^2\lambda_n t}=b_ne^{-{c^2{\left( {\frac{{n\pi }}{L}} \right)^2}}t}=b_ne^{-{{\left( {\frac{{cn\pi }}{L}} \right)^2}}t}
luego
u_n(x,t)=c_ne^{-{{\left( {\frac{{cn\pi }}{L}} \right)^2}}t}\operatorname{sen}\left({\dfrac{{n\pi }}{L}}x\right).
y la solución general es
\boxed{\color{blue}u(x,t) = \sum\limits_{n = 1}^\infty {{c_n}{e^{ – {{\left( {\frac{{cn\pi }}{L}} \right)}^2}t}}\operatorname{sen}\left({\dfrac{{n\pi }}{L}}x\right)}.}
Para determinar los coeficientes c_n de la condición u(x,0)=f(x) tenemos
f(x) = \sum\limits_{n = 1}^\infty {{c_n}\operatorname{sen} \left({\dfrac{{n\pi }}{L}}x\right)}
y por lo tanto son los coeficientes de Fourier del desarrollo en senos de la función f(x) en el intervalo [0,L].
{c_n} = \displaystyle\dfrac{2}{L}\int_0^L {f(x)} \operatorname{sen} \left({\dfrac{{n\pi }}{L}}x\right)\,dx.
Ejemplo: Hallar la solución del problema
\left\{ {\begin{array}{l} {{u_t} – 2{u_{xx}} = 0}&{0 < x < \pi,\;t > 0,} \\ {u(x,0) = x}&{0 < x < \pi,} \\ {u(0,t) = 0}&{t > 0,} \\ {u(\pi,t) = 0}&{t > 0.} \end{array}} \right.\;
Como tenemos que c^2=2 y L=\pi, la solución es
u(x,t) = \sum\limits_{n = 1}^\infty {{c_n}{e^{ – 2{n^2}t}}\operatorname{sen} nx}
donde c_n son los coeficientes de Fourier del desarrollo en senos de la función f(x)=x en el intervalo [0,\pi].
\begin{gathered}{c_n} = \dfrac{2}{\pi }\int_0^\pi x \operatorname{sen} nxdx = – \dfrac{2}{{\pi n}}\left[ {x\cos nx} \right]_0^\pi + \underbrace {\dfrac{2}{{\pi n}}\int_0^\pi {\cos nxdx} }_0\\ \left. {\begin{array}{c} {u = x}&{dv = \operatorname{sen} nx} \\ {du = dx}&{v = – \dfrac{1}{n}\cos nx} \end{array}} \right\}\quad = – \dfrac{2}{{\pi n}}\left( {\pi {{( – 1)}^n}} \right) = \dfrac{{2 \cdot {{( – 1)}^{n + 1}}}}{n} \end{gathered}
concluimos que la solución es
\boxed{\color{blue}u(x,t)=\sum\limits_{n = 1}^\infty {\dfrac{{2 \cdot {{( – 1)}^{n + 1}}}}{n}{e^{ – 2{n^2}t}}\operatorname{sen} nx}.}
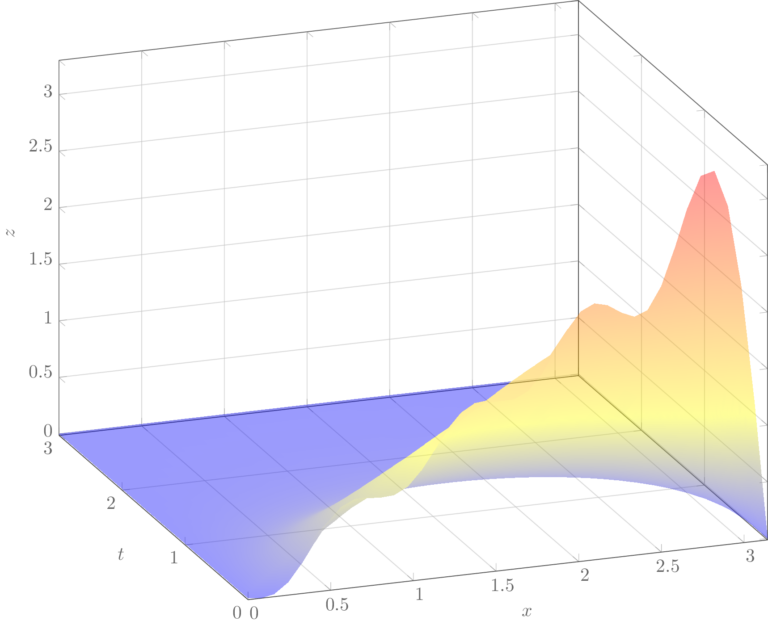
La grafica de la superficie solución es
Si la temperatura en los extremos no es cero, pongamos por ejemplo u(0,t)=T_0 y u(L,t)=T_L podemos transformar el problema mediante el cambio de variable
w(x,t)=u(x,t)-r(x)
donde r(x) es la recta que pasa por los punto \left(0,T_0\right) y \left(L,T_L\right)
\dfrac{x}{L}=\dfrac{y-T_0}{T_L-T_0}\Rightarrow y=r(x)=T_0+\dfrac{x}{L}\left(T_L-T_0\right)
de forma que ahora w(0,t)=w(L,t)=0 y w(x,0)=u(x,0)-r(x)=f(x)-r(x).
Además, w_t=u_t y w_{xx}=u_{xx} y el problema se transforma en
\left\{ {\begin{array}{ll} {{w_t} – c^2{w_{xx}} = 0}&{0 < x < L,\;t > 0,} \\ {w(x,0) = f(x)-r(x)}&{0 < x < L,} \\ {w(0,t) = 0}&{t > 0,} \\ {w(L,t) = 0}&{t > 0,} \end{array}} \right.\;
Ejemplo: Resolver el problema
\left\{ {\begin{array}{ll} {{u_t} – {u_{xx}} = 0}&{0 < x < 1,\;t > 0,} \\ {u(x,0) = 1}&{0 < x < 1,} \\ {u(0,t) = 1}&{t > 0,} \\ {u(1,t) = 0}&{t > 0,} \end{array}} \right.\;
En este caso tenemos que r(x)=1+x(0-1)=-x+1 y el problema se transforma en
\left\{ {\begin{array}{l} w_t – w_{xx}= 0 \\ w(x,0) = -x \\ w(0,t) = 0\\ w(1,t) = 0. \end{array}} \right.\;
La solución de este problema es entonces
w(x,t) = \sum\limits_{n = 1}^\infty {{c_n}{e^{ – {n^2}{\pi ^2}t}}\operatorname{sen} \left( {n\pi x} \right)}
donde c_n son los coeficientes de Fourier del desarrollo en senos de la función -x en el intervalo [0,1].
\begin{array}{l} {c_n} = \displaystyle2\int_0^1 { – x} \operatorname{sen} n\pi xdx = \frac{2}{{\pi n}}\left[ {x\cos n\pi x} \right]_0^1 – \underbrace {\frac{2}{{\pi n}}\int_0^1 {\cos nxdx} }_0\; = \frac{2}{{\pi n}}{{{( – 1)}^n}}\, \\ \left. {\begin{array}{c} {u = x} & {dv = – \operatorname{sen} n\pi x} \\ {du = dx} & {v = \dfrac{1}{n}\cos n\pi x} \\ \end{array} } \right\}\;\\ \end{array}
de forma que
w(x,t) = \sum\limits_{n = 1}^\infty {\dfrac{{2{{( – 1)}^n}}}{{n\pi }}} {e^{ – {n^2}{\pi ^2}t}}\operatorname{sen} (n\pi x)
y la solución del problema pedido es
\boxed{\color{blue}u(x,t)=\sum\limits_{n = 1}^\infty {\dfrac{{2{{( – 1)}^n}}}{{n\pi }}} {e^{ – {n^2}{\pi ^2}t}}\operatorname{sen} (n\pi x)+x-1.}
Resolvemos ahora un ejemplo en el que los coeficientes de Fourier están más definidos.
Ejemplo: Utilizar el método de separación de variables para obtener la solución del problema:
\left\{ {\begin{array}{l} {{u_t} – 4{u_{xx}}=0,}& 0<x<10, t>0 \\ u(0,t) = 0, &t>0, \\ u(10,t) = 0,&t>0, \\ u(x,0) =f(x) ,& 0<x<10. \end{array}} \right.\;
con f(x)=5\operatorname{sen} \dfrac{{3\pi x}}{2} + 2\operatorname{sen} \pi x – 7\operatorname{sen} 4\pi x.
En este caso c^2=4 y L=10, entonces la solución será de la forma
u(x,t) =\sum\limits_{n = 1}^\infty {{c_n}{e^{ – {{ {\frac{{4n^2\pi^2 }}{100}} }}t}}\operatorname{sen}\left({\dfrac{{n\pi }}{10}}x\right)}=\sum\limits_{n = 1}^\infty {{c_n}{e^{ – {{ {\frac{{n^2\pi^2 }}{25}} }}t}}\operatorname{sen}\left({\dfrac{{n\pi }}{10}}x\right)}.
Donde c_n son los coeficientes de Fourier de la función del desarrollo en senos f(x). Como la función ya está expresada en senos y solo hay tres términos entonces
\begin{darray}{l} \frac{3}{2} = \frac{n}{{10}} \Rightarrow n = 15 \Rightarrow \frac{{{n^2}{\pi ^2}}}{{25}} = \frac{{225{\pi ^2}}}{{25}} = 9{\pi ^2}\\ 1 = \frac{n}{{10}} \Rightarrow n = 10 \Rightarrow \frac{{{n^2}{\pi ^2}}}{{25}} = \frac{{100{\pi ^2}}}{{25}} = 4{\pi ^2} \\ 4 = \frac{n}{{10}} \Rightarrow n = 40 \Rightarrow \frac{{{n^2}{\pi ^2}}}{{25}} = \frac{{1600{\pi ^2}}}{{25}} = 64{\pi ^2} \\ \end{darray}
Además c_{10}=2,\,c_{15}=5,\,c_{40}=-7 y c_n=0\,\forall n\neq10,15,40. La solución es pues
\boxed{\color{blue}u(x,t)=2e^{-4\pi^2t}\operatorname{sen}\pi x+5e^{-9\pi^2t}\operatorname{sen}\dfrac{3\pi x}{2}-7e^{-64\pi^2t}\operatorname{sen}4\pi x.}
