El ensayo de tracción es sin duda el más importante de los ensayos mecánicos realizados en ingeniería de materiales. Es un ensayo simple, sencillo de realizar, pero muy completo, dando una gran cantidad de información sobre el comportamiento mecánico y las propiedades de un material.
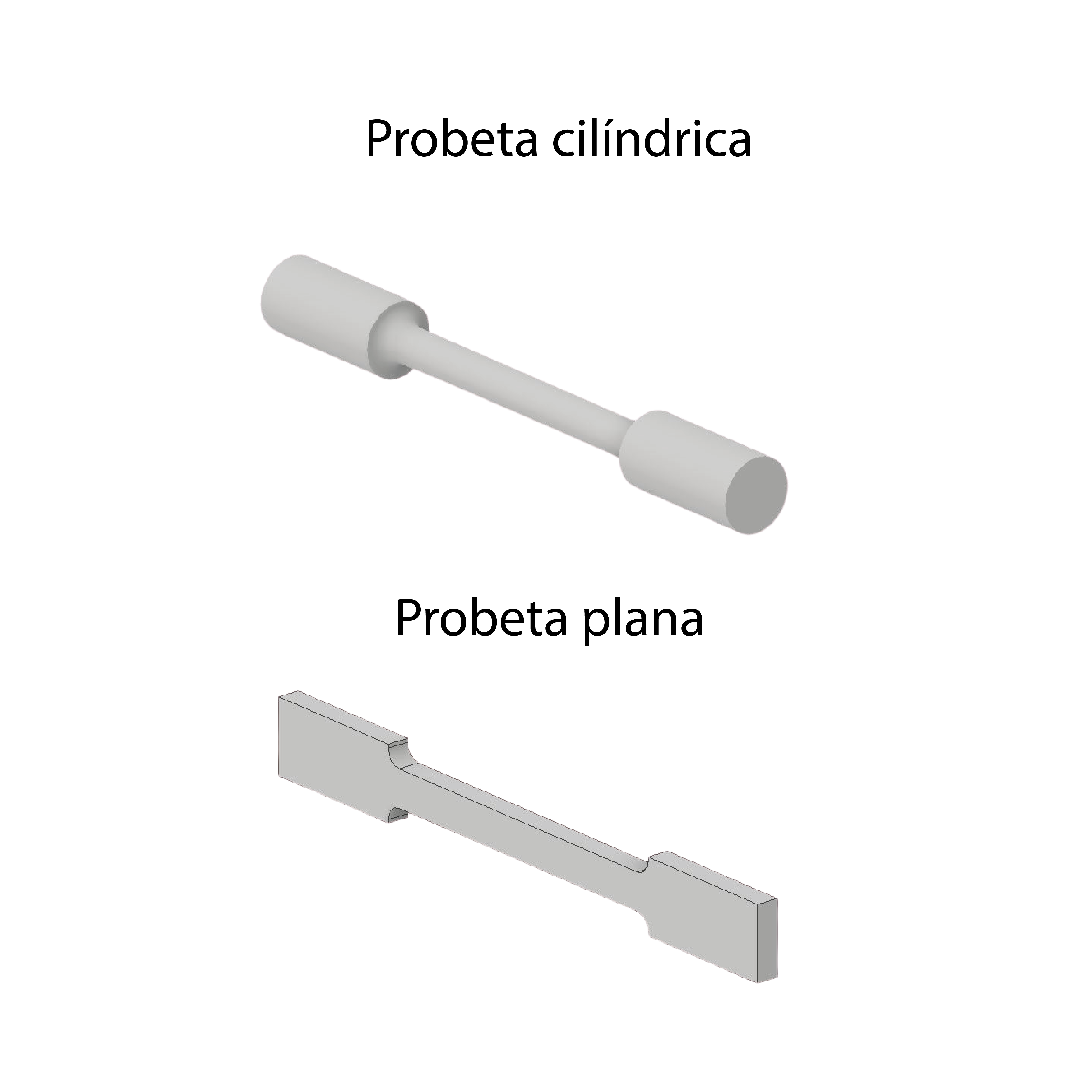
El ensayo consiste en producir un estiramiento, mediante un esfuerzo de tracción, a una probeta del material que se quiere analizar. Las probetas utilizadas están normalizadas (tienen unas medidas estándar buscando que todos los ensayos se realicen bajo las mismas condiciones), asegurando una zona central de sección constante y con dos cabezas mucho más anchas que la zona central. Las probetas pueden ser planas o cilíndricas.
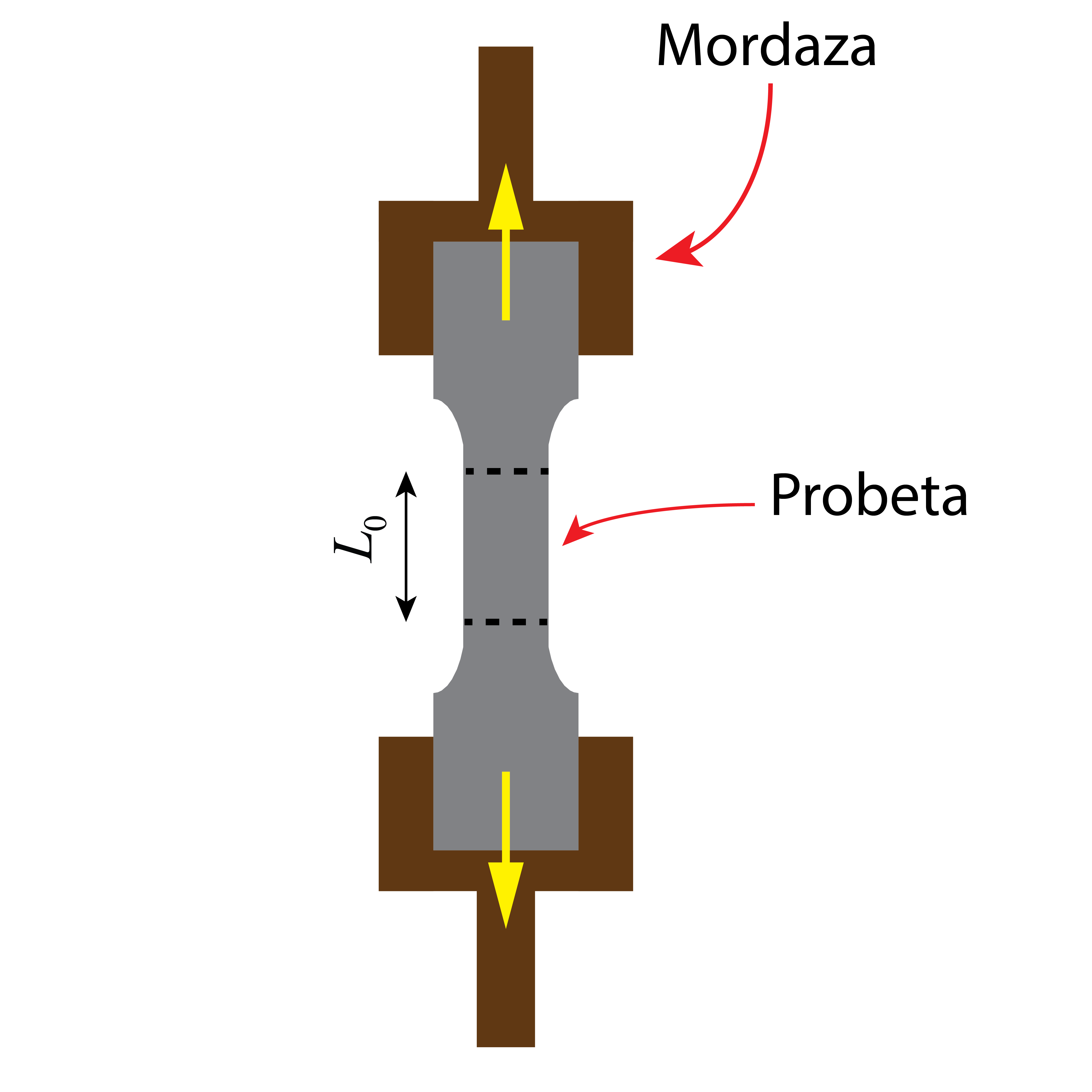
Para realizar el ensayo es necesario disponer de una máquina de tracción (o máquina universal de ensayos). Esta máquina es capaz de producir la deformación en la probeta, estirándola para generar la deformación. La probeta se sujeta en la máquina mediante dos mordazas que aprietan las cabezas, de modo que la probeta no se resbale.
Una de las mordazas (normalmente la inferior) se queda fija, mientras la otra mordaza aplica un desplazamiento a una velocidad controlada (también normalizada), produciendo una separación entre ambas mordazas e incrementando la longitud de la probeta. En todo momento, la máquina registra automáticamente el desplazamiento y la fuerza aplicada.
Durante el ensayo, la deformación que se produce en la probeta está homogéneamente repartida por toda su longitud, observando como la sección se reduce (se vuelve más estrecha o fina) conforme se incrementa su longitud. La deformación es homogénea hasta que se alcanza el punto de fuerza máxima. En ese momento, en materiales dúctiles, aparece el fenómeno de la estricción, localizando una zona en la que se produce una reducción acelerada de la sección, conduciendo a la rotura. El ensayo finaliza cuando la probeta se rompe. Se dará como válido si la rotura de la probeta ocurre en la zona central, la de sección constante, siendo nulo si la rotura se produce cerca de la zona de empalme con las cabezas.
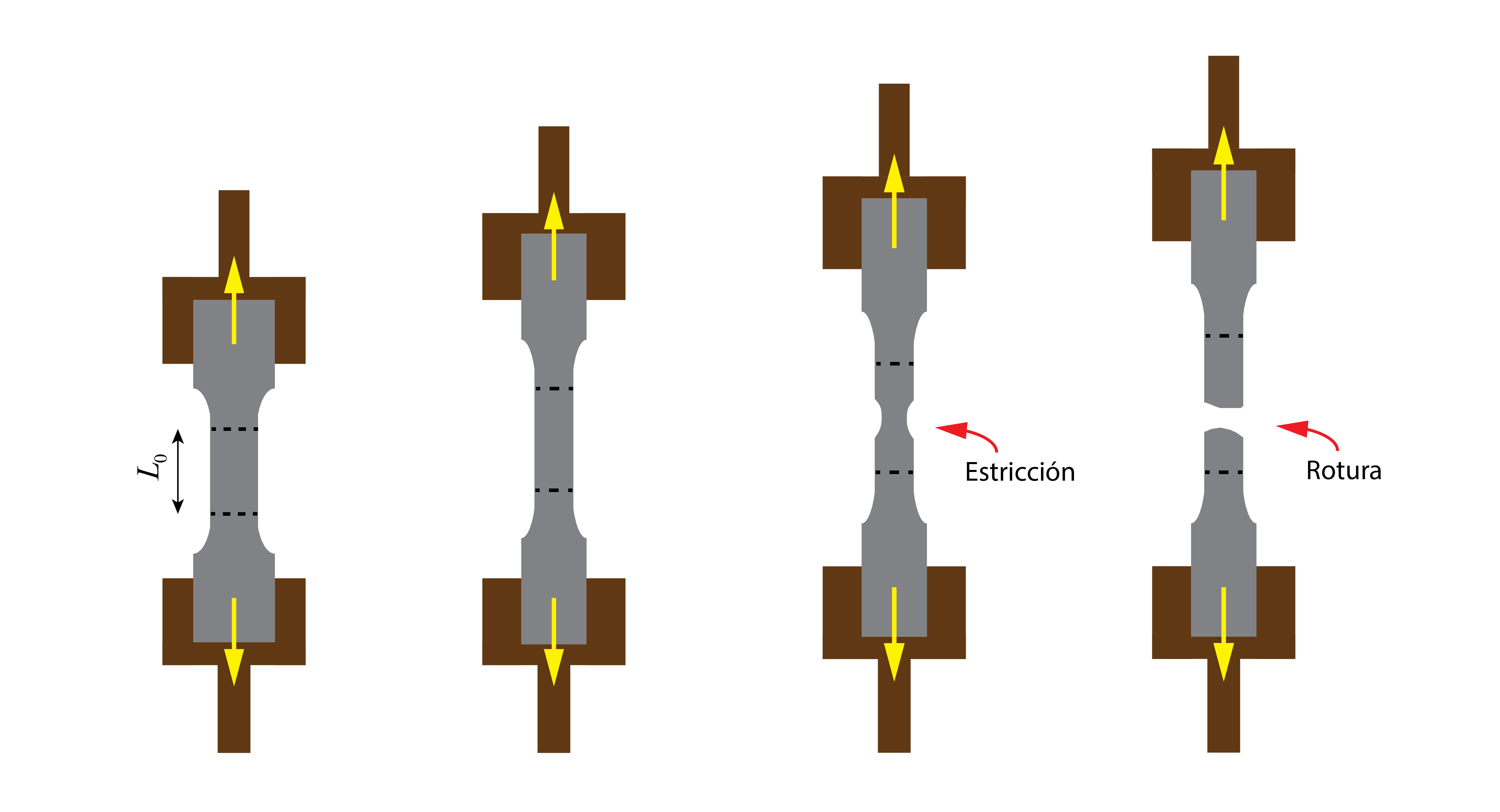
A partir de los datos registrados por la máquina, se construye la gráfica fuerza-alargamiento, en la que ya se distinguen dos zonas claramente diferenciadas. Sin embargo, esta gráfica no es normalmente utilizada para comprender el comportamiento del material, ya que el resultado obtenido depende de una variable introducida en el ensayo, el área transversal de la probeta.
Como es obvio, la probeta resistirá una fuerza mayor cuanto más grande sea su sección transversal, es decir, cuanto más gruesa sea. Desde el punto de vista de la ingeniería de materiales, resulta mucho más interesante conocer la tensión máxima que un material puede soportar, ya que con este valor, la fuerza puede calcularse en función de la sección que tenga la pieza.
Por este motivo, en lugar de trabajar con la curva fuerza-alargamiento, se obtiene la curva tensión-deformación ingenieril. La tensión, σ, se calcular dividiendo la fuerza, F, registrada por la máquina entre el área inicial de la sección transversal de la probeta, A_0.
\sigma = \dfrac{F}{{{A_0}}}
La deformación, ε, producida en el material se obtiene, a partir del alargamiento medido por la máquina, como
\varepsilon = \dfrac{{\Delta L}}{{{L_0}}} = \dfrac{{L – {L_0}}}{{{L_0}}}
Donde L es la longitud en cada instante y L_0 es la longitud inicial de la probeta en la zona de sección uniforme. Según esta definición, la deformación es adimensional (no tiene unidades) y representa el porcentaje de incremento de longitud respecto de la longitud inicial.
Aunque la curva tensión-deformación presente una forma semejante a la gráfica fuerza-alargamiento, no depende de la geometría de la probeta, por lo que los resultados son únicamente función del material y sus propiedades mecánicas.
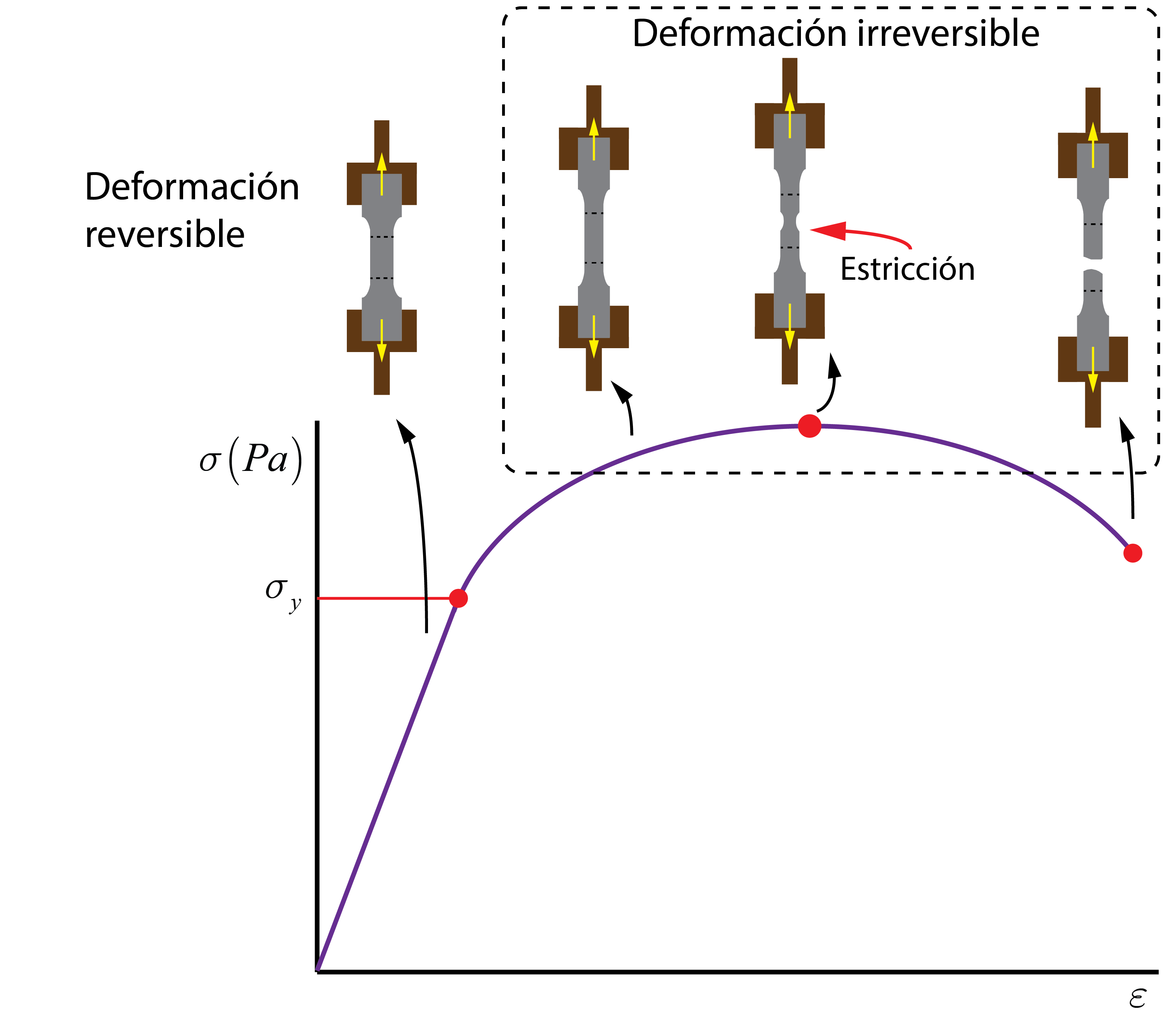
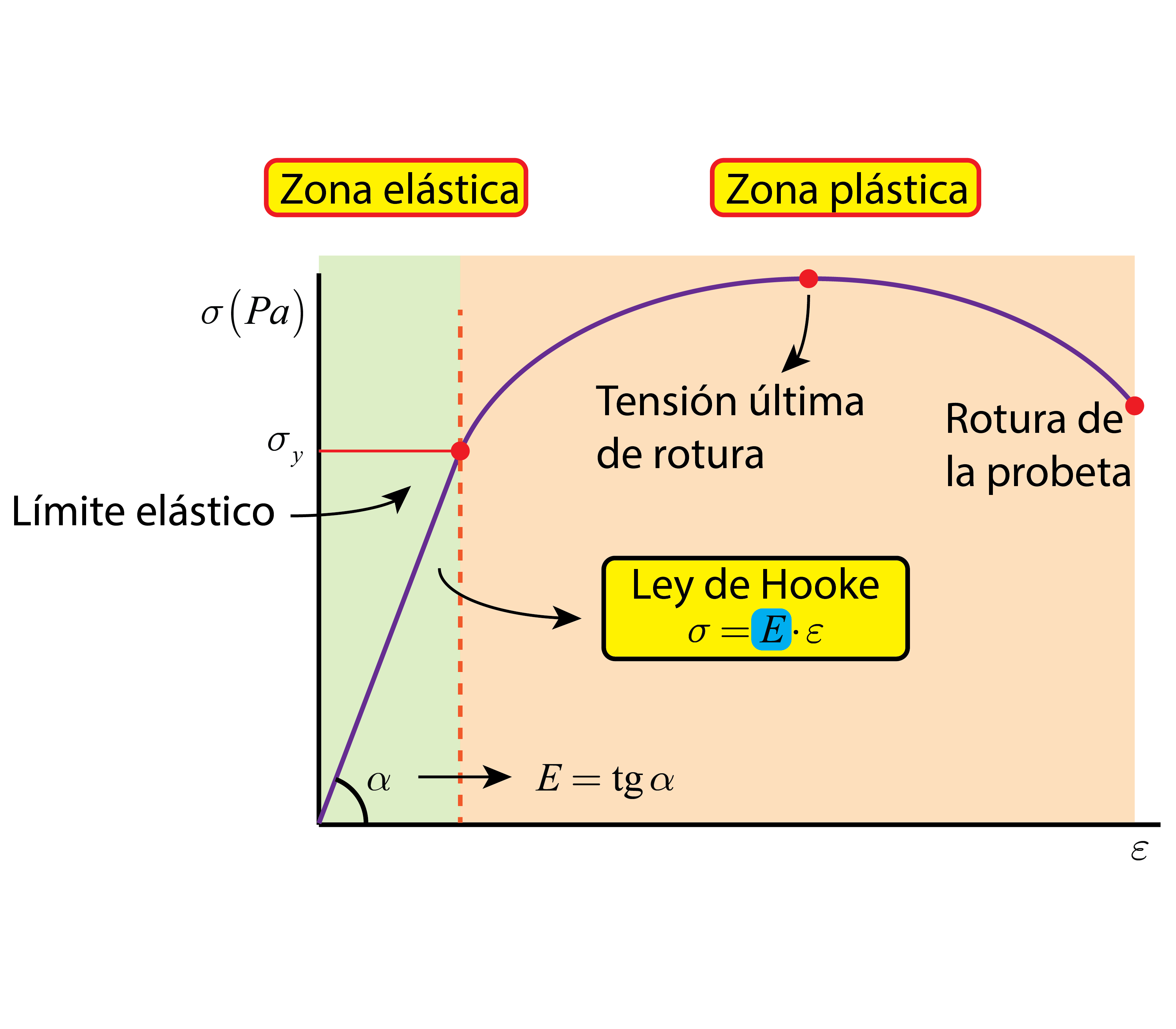
Se identifican dos zonas claramente diferenciadas. En la primera zona, la tensión es linealmente proporcional a la deformación. Es conocida como zona elástica del material. Por el contrario, a partir de un punto llamado límite elástico, la relación entre la tensión y la deformación deja de ser lineal. Se dice que la curva entra en la zona plástica.
En la zona elástica, el material se comporta como un muelle, ya que la relación entre tensión y deformación es lineal, siguiendo la Ley de Hooke. Además, la deformación en esta zona es reversible, se recupera tras el cese de la carga. Es decir, si después de deformar el material, se deja de aplicar la fuerza, el material recupera su estado inicial.
Ley de Hooke \to \sigma = E \cdot \varepsilon
La constante de proporcionalidad que relaciona tensión y deformación es conocida como módulo de Young o módulo elástico, E, definido a partir de la pendiente de la curva tensión-deformación en la zona elástica. Es una constante elástica del material muy importante, ya que aporta información acerca de la rigidez del material, que es la resistencia a la deformación. Cuanto mayor sea el módulo elástico, la pendiente de la zona elástica será mayor, lo que significa que se requiere una tensión más grande para producir la misma deformación. Por ejemplo, los polímeros tienen un bajo módulo elástico comparado con los materiales metálicos.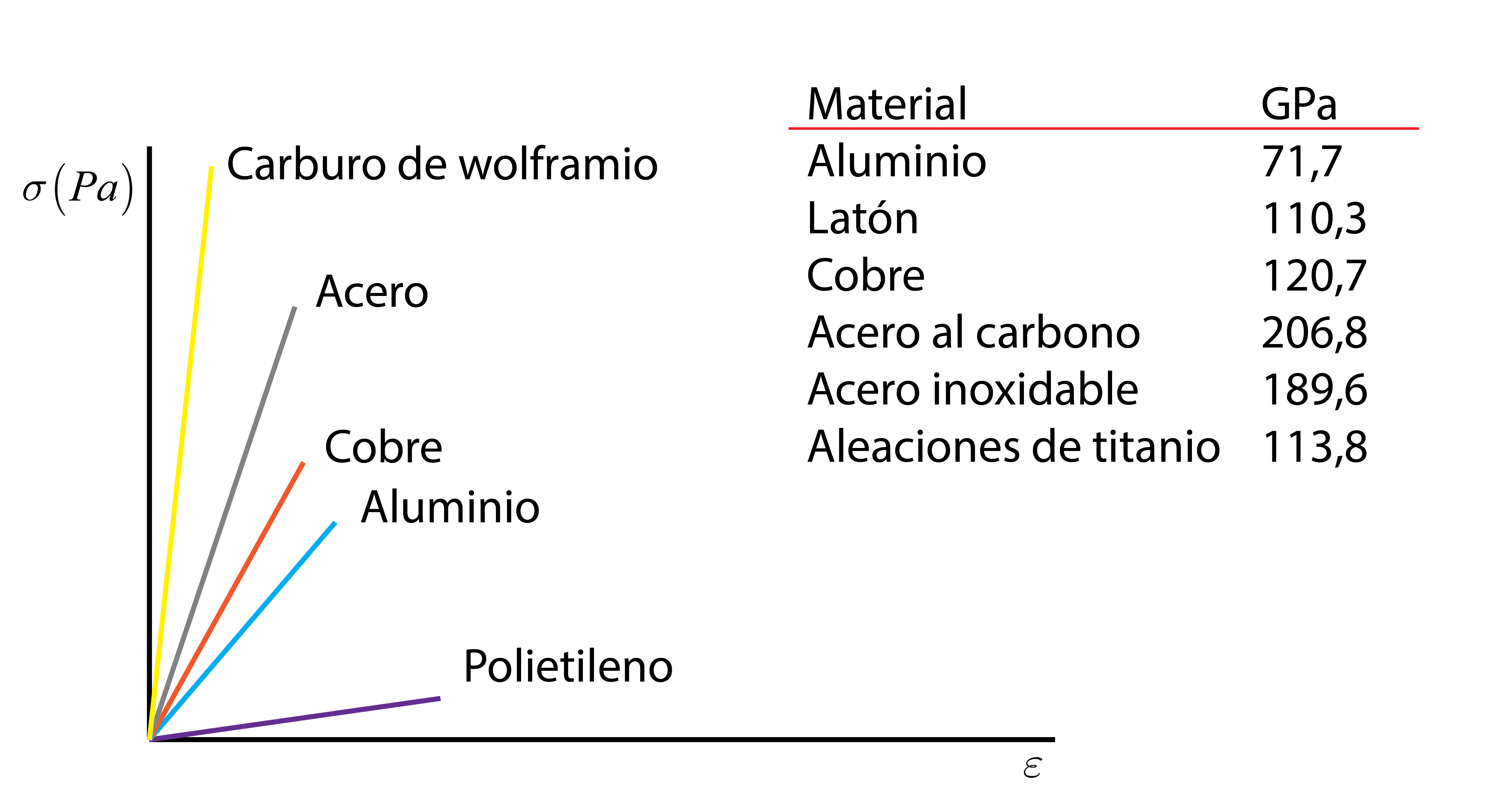
La región elástica finaliza en el límite elástico, que es la tensión máxima que puede aplicarse en el material sin que plastifique. Es decir, a partir de este valor el material entra en zona plástica.
El límite elástico se localiza donde se observa un cambio de pendiente en la curva tensión-deformación. Sin embargo, hay ocasiones en las que no es sencillo apreciar este cambio de tendencia. Por convenio, se define el valor del límite elástico al 0,2% de deformación, trazando una recta paralela a la zona elástica, hasta el valor de corte en la gráfica. Cuanto mayor sea el límite elástico de un material, mayor carga podrá soportar sin deformarse de manera irreversible.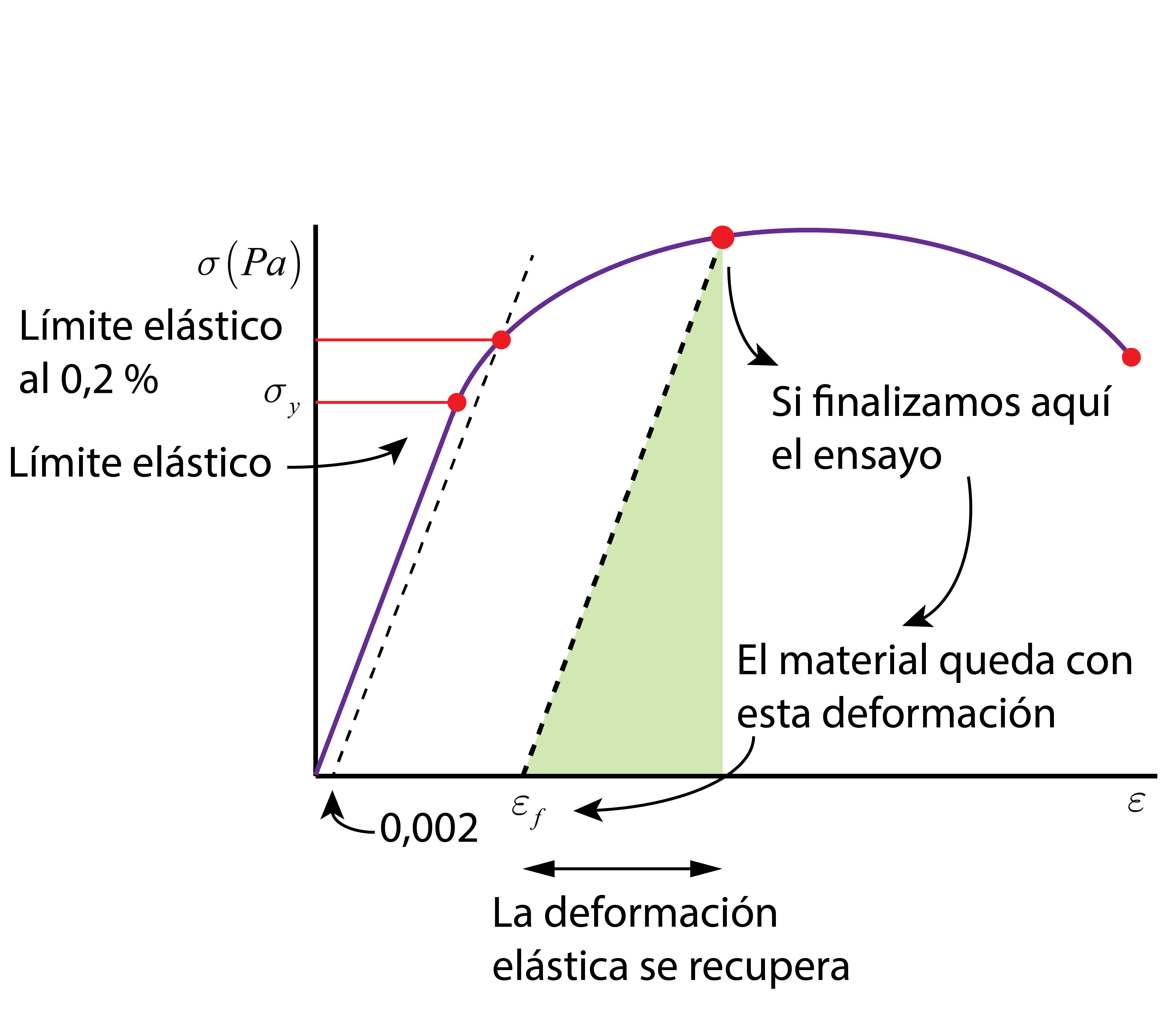
Cuando la tensión aplicada es superior a este límite, el material entra en zona plástica. Aquí, únicamente la deformación elástica será recuperada tras el cese de la carga, quedando el material deformado. Para conocer el estado de deformación después de retirar la carga, hay que descender en la gráfica siguiendo una recta paralela a la zona elástica.
En la zona plástica, la relación entre la tensión y la deformación no es lineal. Al principio, la tensión aumenta, lo que se conoce como endurecimiento por deformación, hasta llegar al valor de tensión última del material, el máximo de la curva. Esta es la resistencia máxima del material. A partir de este valor, se localiza una zona de deformación abrupta, llamada zona de estricción. La sección se reduce rápidamente provocando un descenso en la fuerza hasta llegar al valor de la tensión de rotura.
¿Cuándo un material es dúctil o frágil?
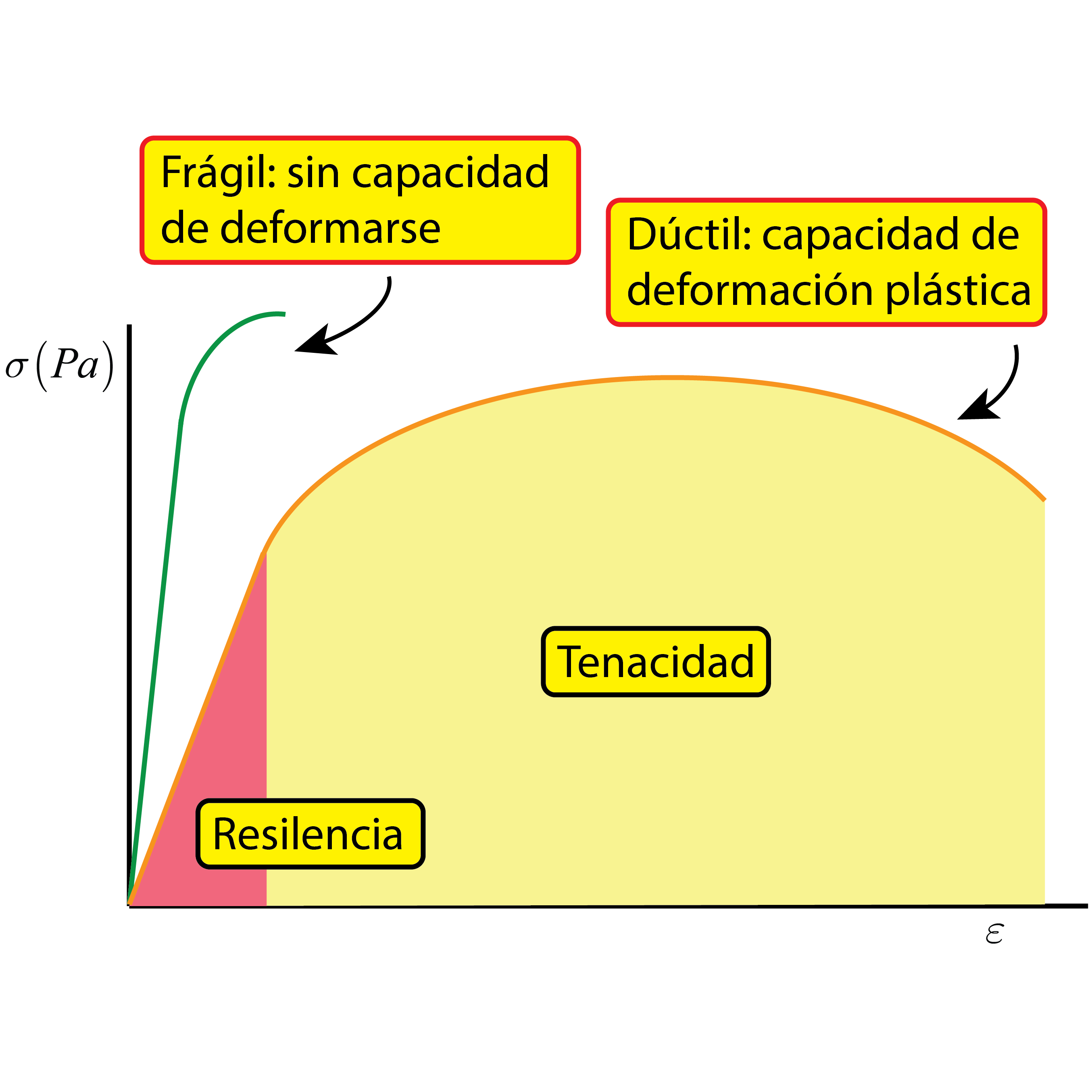
Llegados a este punto es importante hablar de ductilidad, fragilidad y tenacidad. Un material es dúctil si tiene capacidad de deformarse plásticamente antes de la rotura. Será más dúctil cuanto mayor grado de deformación alcance.
Por el contrario, los materiales frágiles no tienen capacidad de deformarse plásticamente, llegando a la rotura en una etapa temprana tras superar el límite elástico y presentando una curva tensión-deformación mucho más corta. En estos casos, tampoco suele aparecer la estricción.
Este hecho es útil para detectar, observando la forma de la rotura, si un material es dúctil o frágil. En un material dúctil, aparecerá una zona de estricción, formando lo que se conoce como una copa y un cono (rotura copa-cono). En cambio, la rotura frágil se caracteriza por no tener deformación, siendo una rotura plana y brillante.
El área bajo la curva representa la energía absorbida por el material, en modo de energía de deformación, hasta la rotura, lo que se conoce como tenacidad del material. La tenacidad relaciona, por lo tanto, tensión y deformación, ya que para que un material sea considerado como tenaz, debe ser capaz de alcanzar un grado de deformación elevado y resistir tensiones altas. El área bajo la curva en la zona elástica es la energía necesaria para deformar elásticamente el material, conocida como resiliencia.
Resumiendo, el ensayo de tracción aporta una gran cantidad de información sobre las características mecánicas del material. De un ensayo, pueden obtenerse las siguientes propiedades:
- Límite elástico
- Módulo elástico
- Tensión última de rotura
- Deformación en tensión última
- Tensión de rotura
- Deformación de rotura
- Valoración de la ductilidad/fragilidad.
Además, para algunos materiales, como el caso del acero, la curva puede presentar una forma algo distinta, encontrando una tercera región llamada zona de fluencia. Esta región se sitúa entre la zonas elástica y plástica. Al superar el límite elástico, se produce un incremento de la deformación sin aumentar la tensión aplicada, lo que se conoce como fluencia. La tensión en el punto de inicio se llama límite de fluencia y la deformación producida en esta zona es también irreversible.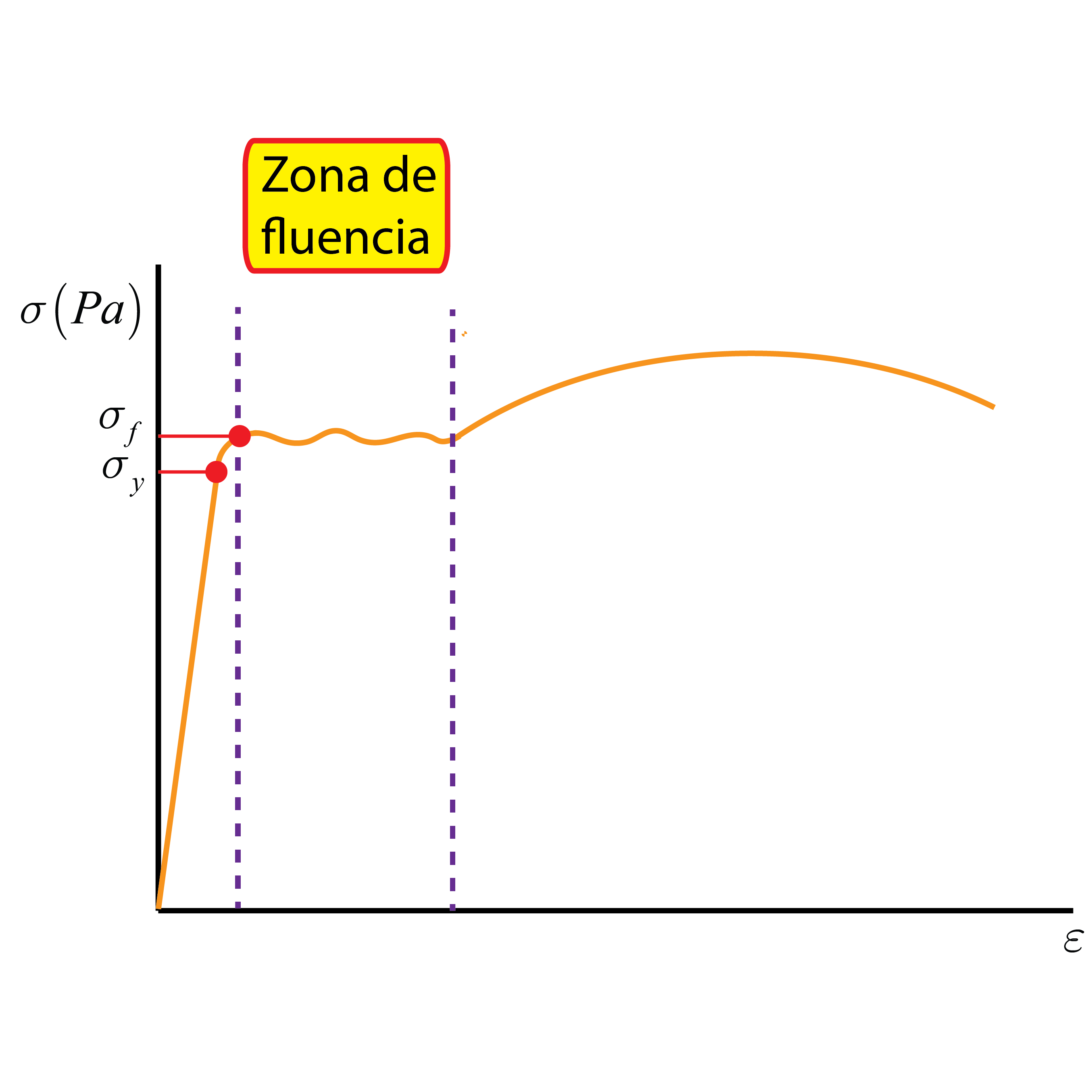
Los materiales isótropos son aquellos que presentan las mismas propiedades mecánicas en todas las direcciones del espacio, como la mayoría de los metales. Sin embargo, hay materiales que no cumplen esta característica, como la madera, los materiales compuestos o el hormigón. Sus propiedades mecánicas varían según la dirección de aplicación del esfuerzo. Son conocidos como materiales ortótropos, siendo necesario caracterizar sus propiedades en todas las direcciones del espacio.
Como podemos observar, conocer todos estos datos sobre los materiales es muy importante, ya que nos permite decidir qué material utilizar para cada aplicación. Normalmente, para cálculos estructurales, los materiales trabajan únicamente en zona elástica sin superar el límite elástico. Es decir, siempre se trabaja con la hipótesis de que las deformaciones serán reversibles, teniendo un gran margen de seguridad respecto de la rotura.
En otros casos, como los procesos de deformación plástica (extrusión, laminación, forja…), se lleva a los materiales hasta la zona plástica. Esto es necesario, ya que estos procesos consisten en deformar los materiales para conseguir una geometría final distinta a la inicial, lo que se logra si las deformaciones son irreversibles.
Como último apunte, la curva tensión-deformación descrita en este artículo es conocida como curva ingenieril, pero no es una curva totalmente realista del comportamiento del material. Si tenéis intriga en saber cuál es la curva tensión-deformación verdadera os sugiero clicar en este enlace.
También os animo a ver el siguiente vídeo donde se detallan todos estos conceptos con animaciones!!