El esfuerzo cortante es muy importante en ingeniería, ya que está presente en la mayoría de estructuras, piezas y componentes mecánicos e, incluso, es el fenómeno principal que aparece en procesos de fabricación como el cizallado o el troquelado.
En este artículo te explicamos en qué consiste, qué tensiones y deformaciones genera y cómo calcularlo. También hay un vídeo sobre el tema al final del artículo.
Para realizar la explicación, vamos a ayudarnos de una barra, la cual tiene aplicadas dos fuerzas iguales en sentido contrario y perpendiculares a su eje longitudinal, separadas una distancia muy pequeña (entiéndase muy pequeña como una distancia casi insignificante, pero lo suficiente para que las fuerzas no estén aplicadas en la misma sección).
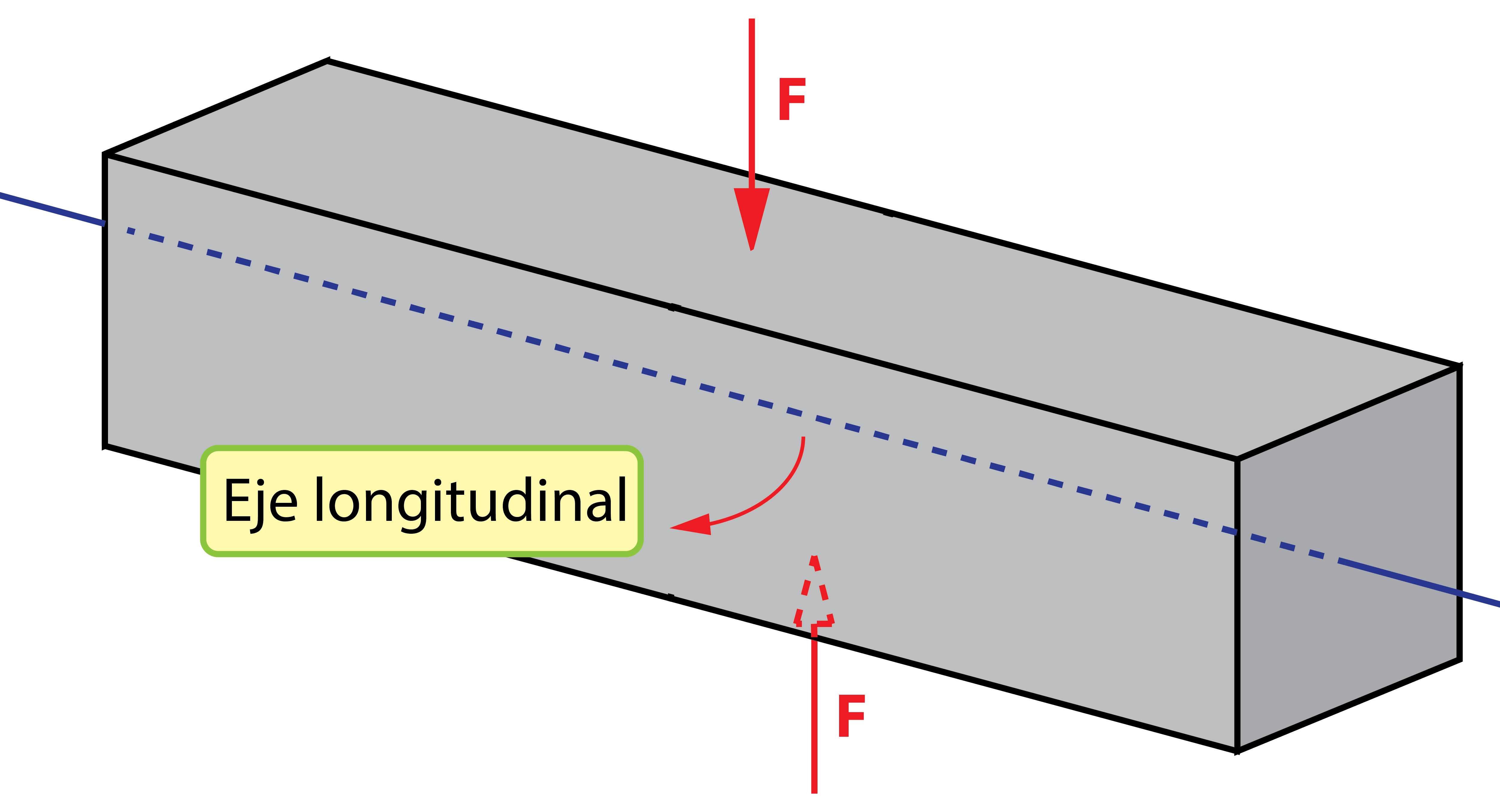
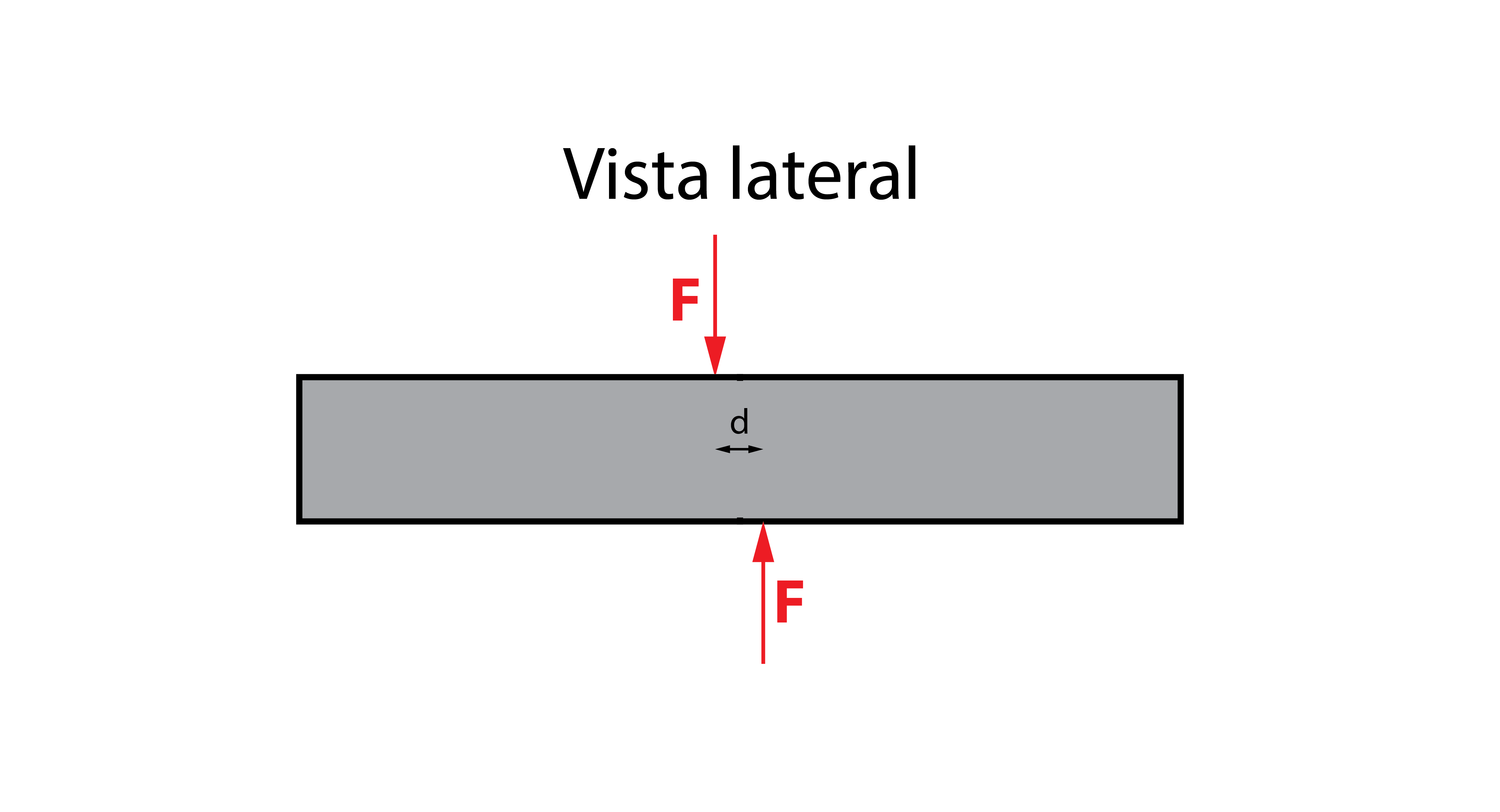
En la barra se está produciendo un esfuerzo cortante o cizalladura, que tiende a cortar la barra transversalmente, a cizallarla. Para entender qué está ocurriendo internamente en el material, es necesario analizar por separado una mitad de la barra, excluyendo la otra parte.
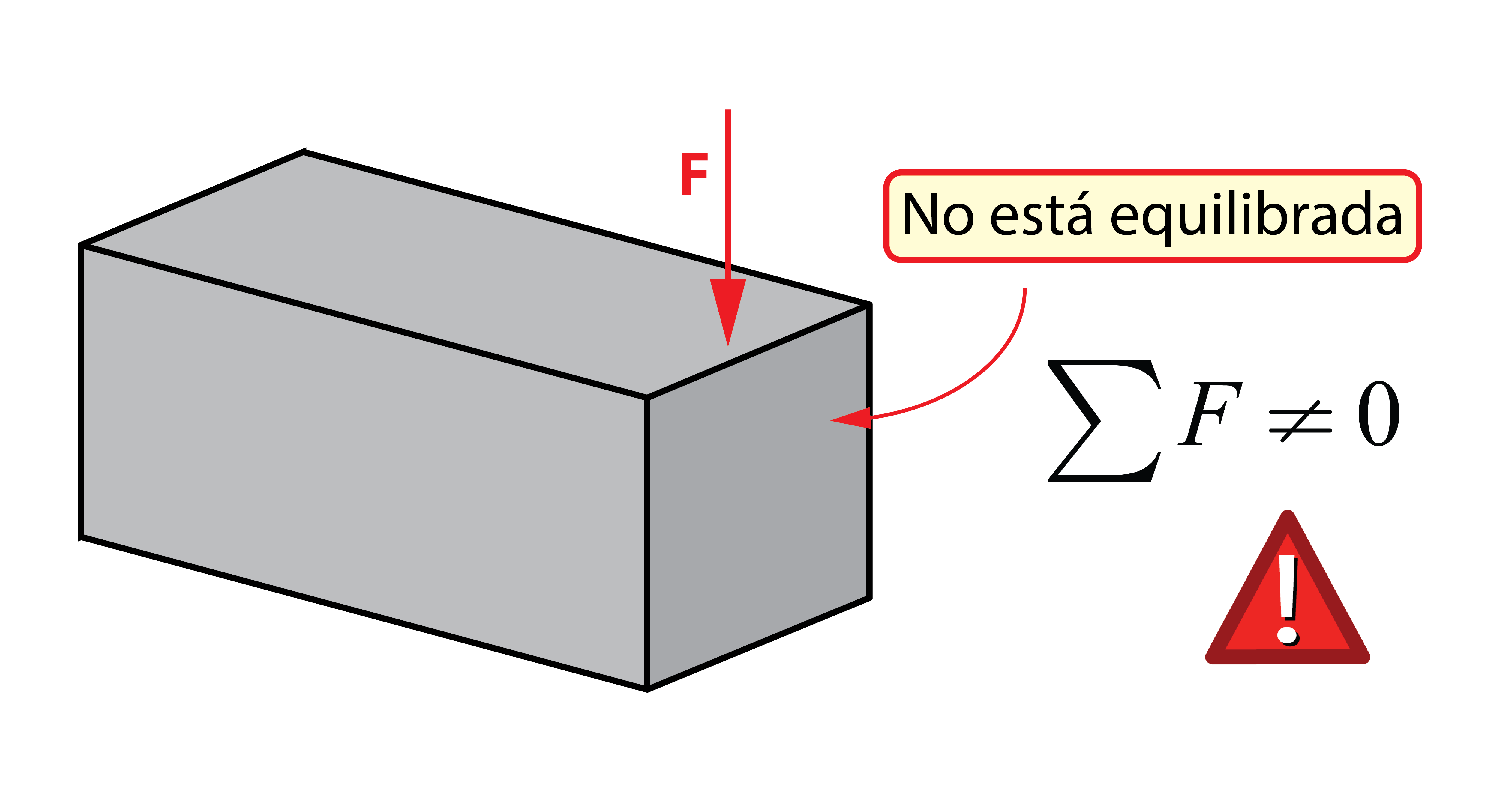
Al eliminar del estudio la mitad derecha, la parte izquierda no se encuentra en equilibrio estático. La fuerza F no está equilibrada, por lo que la barra se desplazaría en la dirección de aplicación de la carga. Para conseguir el equilibrio, es necesario que aparezca una tensión interna (reacción interna del sólido ante la aplicación de la carga), tangente al plano de corte y en sentido opuesto a F. Esta tensión es conocida como Tensión Tangencial.
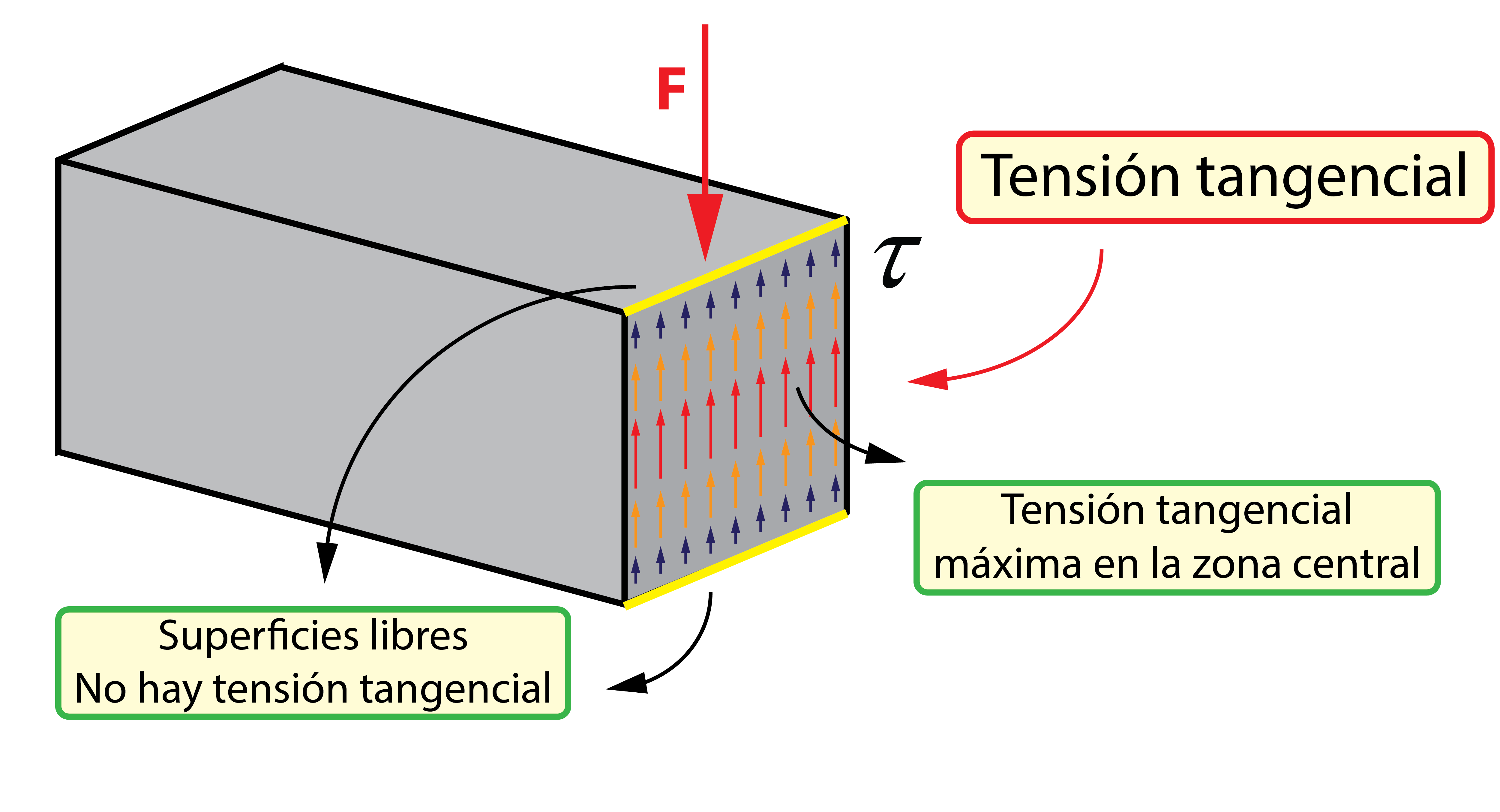
La tensión tangencial, al contrario de lo que ocurre con la tensión normal generada en los esfuerzos de tracción y compresión, no está uniformemente distribuida por la sección de la barra. La tensión tangencial es nula en las fibras superior e inferior del perfil y máxima en la zona central de la sección. El valor medio de la tensión tangencial se puede estimar calculando el balance estático, dividiendo la fuerza aplicada entre el área de la sección transversal de la barra, A.
\sum {\overrightarrow F } = 0
F = \tau \cdot A
\tau = \dfrac{F}{A}
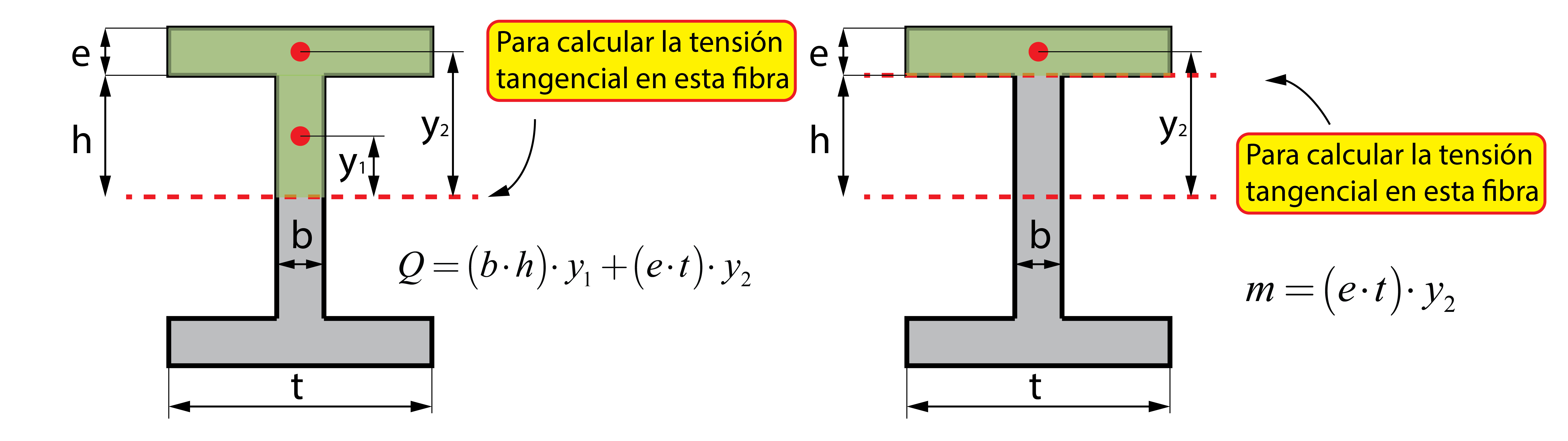
La tensión tangencial máxima en el centro de la sección puede calcularse utilizando la Ecuación de Collignon (no está claro que la autoría sea suya o de Dmitri Zhuravski), a partir del cortante aplicado en la sección, V, el primer momento de área o momento estático, Q, el momento de inercia de la sección, I, y el espesor de la sección en la zona central, b.
\tau = \dfrac{{V \cdot Q}}{{I \cdot b}}
Esta ecuación también puede utilizarse para estimar la tensión tangencial en cualquier otra posición del perfil, obteniendo el momento estático de la zona limitada entre la fibra externa y la posición donde se realiza el cálculo, m, y el espesor de la sección en dicha posición.
\tau = \dfrac{{V \cdot m}}{{I \cdot b}}
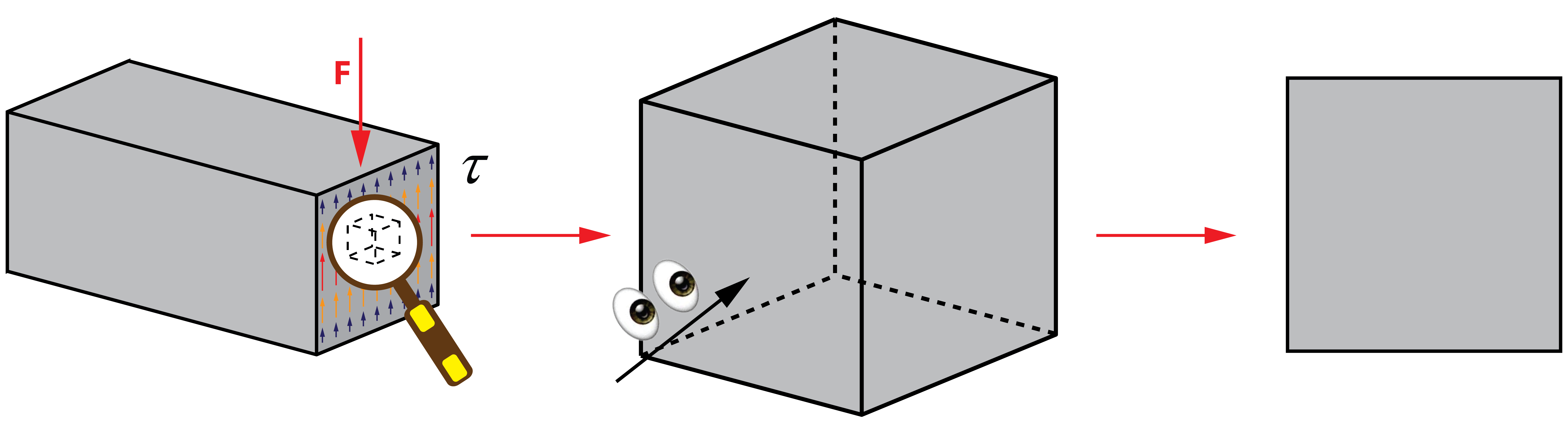
Como es lógico, el esfuerzo cortante, además de producir una tensión tangencial, genera una deformación en la pieza. Recuérdese que los conceptos de tensión y deformación siempre están ligados en mecánica de materiales. Con el objetivo de entender cómo se produce la deformación cortante, se analiza un elemento diferencial del interior del sólido (un trocito muy pequeño del material).
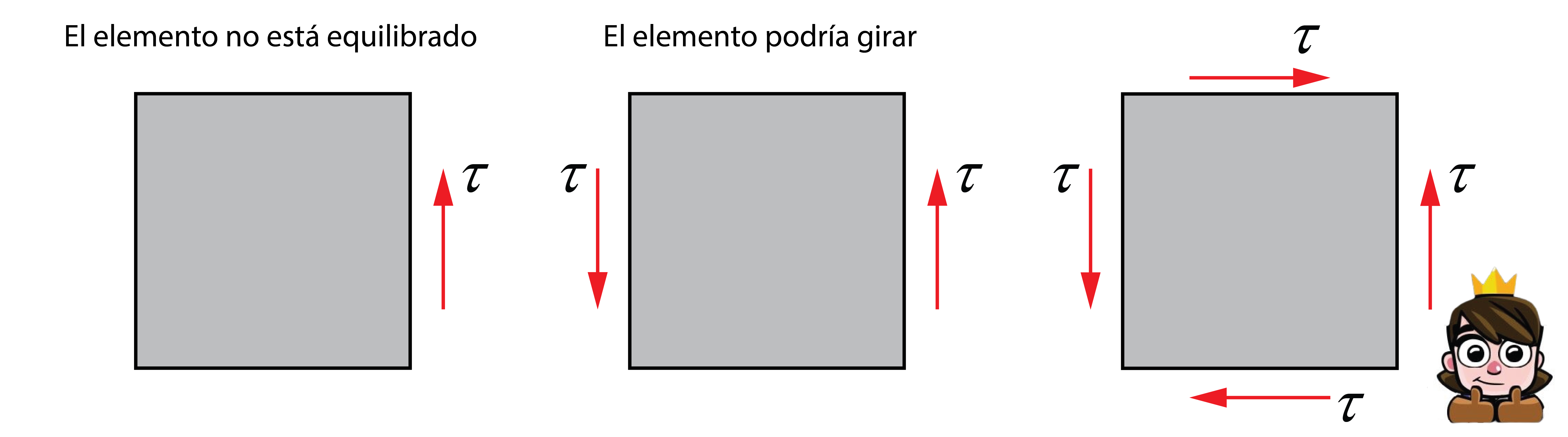
El elemento debe estar en equilibrio estático, por lo que es necesario que aparezca una tensión cortante igual en sentido contrario en el lado opuesto. Sin embargo, esto generaría el giro del elemento, lo que se evita con la aparición de los tensiones tangenciales adicionales en la dirección horizontal. La generación de tensiones tangenciales en los cuatro lados del elemento explica cómo las tensiones tangenciales se distribuyen entre fibras de una misma sección y se transportan entre las distintas secciones de la barra.
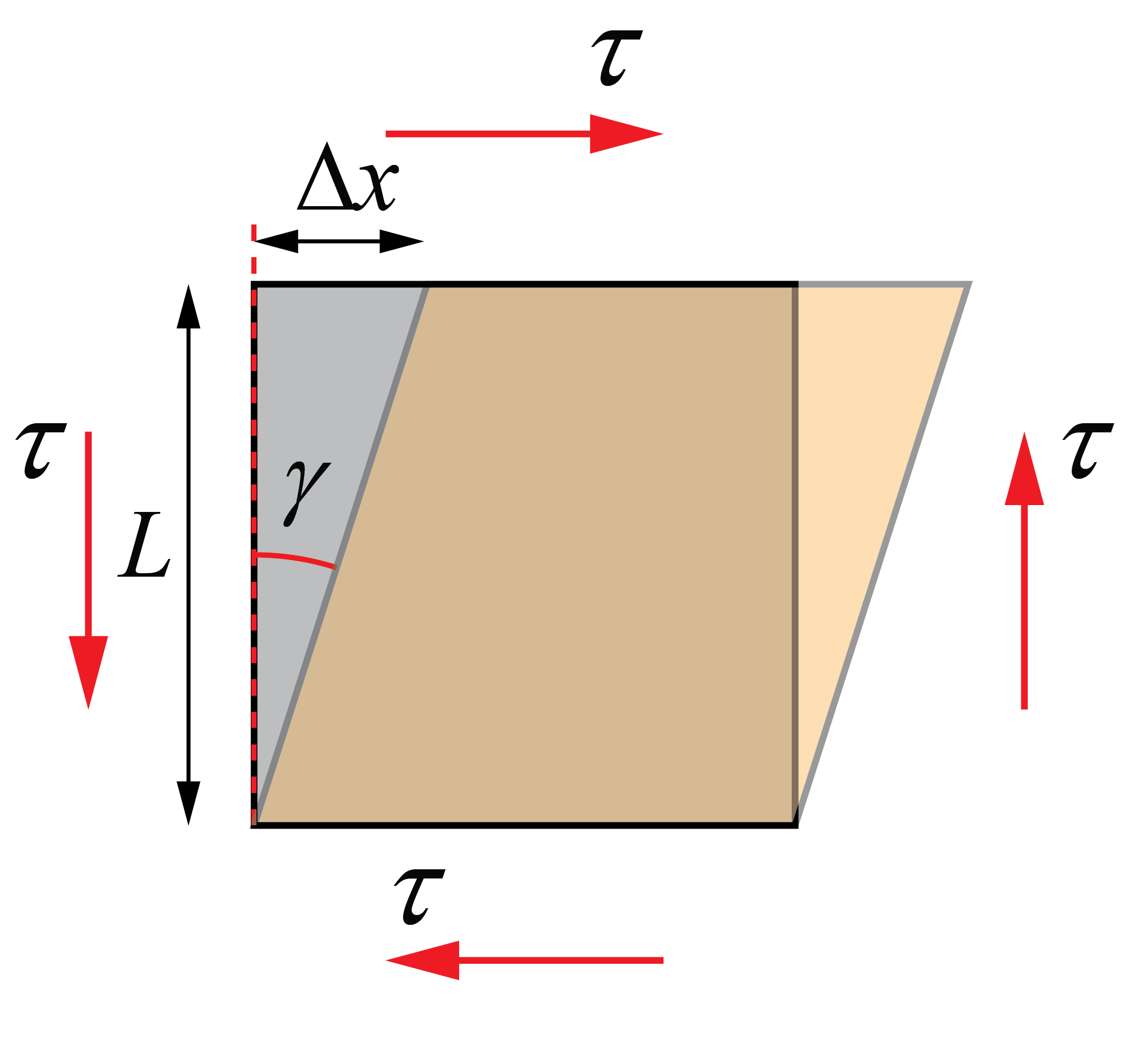
Esta configuración de tensiones tangenciales produce una deformación en el elemento, conocida como deformación cortante, y definida por el ángulo γ. Su valor se deduce a partir del desplazamiento horizontal del elemento, entre su longitud inicial, teniendo en cuenta que, para ángulos pequeños (lo que ocurre en la hipótesis de pequeñas deformaciones bajo la que se estudian estos fenómenos), el ángulo se aproxima al valor de su tangente. (Pd: también aparecen tensiones y deformaciones cortantes en el esfuerzo de torsión. Os dejo un enlace a un artículo sobre el tema.)
Deformación cortante
\gamma=\dfrac{\Delta x}{L}
Relación entre tensión tangencial y deformación cortante
La tensión tangencial y la deformación cortante no toman valores cualesquiera, sino que están ligadas por las propiedades mecánicas del material. Recuérdese que, en la zona elástica del material, que es aquella correspondiente a valores de tensión inferiores al límite elástico, la relación entre tensión-deformación es lineal.
En zona elástica, la deformación producida por la carga es recuperada tras el cese de su aplicación, recuperando el material sus condiciones iniciales y volviendo la pieza a su estado original.
En zona elástica se cumple la Ley de Hooke: la tensión tangencial es igual a la deformación cortante por el módulo de elasticidad transversal del material, G.
\tau = G \cdot \gamma
El módulo de elasticidad transversal es una propiedad del material que, en caso de materiales isótropos (aquellos cuyas propiedades no varían con la dirección de aplicación del esfuerzo), se puede deducir a partir del módulo elástico, E, y el coeficiente de Poisson, ν.
G = \dfrac{E}{{2\left( {1 + \upsilon } \right)}}
Cada material presentará una resistencia al cortante distinta. Si la tensión máxima resistente es superada, se provocará la cizalla de la pieza. Esto es lo que ocurre cuando se corta un papel con una tijeras, o cuando se fabrican piezas de chapa mediante procesos de fabricación como el troquelado.
Os animo a ver el siguiente vídeo donde se detallan todos estos conceptos con animaciones!!
