Conocer en qué consiste el esfuerzo de flexión es muy importante para un ingeniero, ya que está presente en la mayoría de mecanismos y estructuras, siendo la mayoría de veces el esfuerzo determinante. En este artículo explicamos los fundamentos físicos y matemáticos básicos de la flexión pura, describiendo las ecuaciones principales para calcularlo. También encontrarás un vídeo explicativo al final.
Para llevar a cabo la explicación, vamos a utilizar como ejemplo una barra a la que se le aplican dos momentos de giro iguales, pero de sentido contrario en sus extremos. Dicho en palabras simples, se dobla la barra cogida por sus extremos.


Esta situación es conocida como flexión pura, ya que no existen otro tipo de fuerzas aplicadas en la barra, por lo que no aparecen esfuerzos cortantes. Lógicamente, la barra sufre una deformación, se flexiona.
Podemos dividir la barra en dos regiones respecto del eje neutro, la región superior y la región inferior. Las fibras de la zona superior acortan su longitud, por lo que están sufriendo un esfuerzo de compresión, mientras que las fibras inferiores se alargan, están sometidas a un esfuerzo de tracción. La línea neutra no sufre ninguno de los esfuerzos, existiendo una transición clara entre una zona a otra.

Cuanto más alejadas se encuentren las fibras del perfil respecto de la línea neutra, mayor será el esfuerzo de tracción o compresión al que están sometidas, es decir, mayor será la tensión normal en esa sección. Recuérdese que los esfuerzos de tracción y compresión se caracterizan por la generación de tensiones normales en la pieza, perpendiculares a la sección de la barra.
Para calcular qué valor toma la tensión normal, σ, en cada posición del perfil es necesario realizar algunas operaciones matemáticas. Tras la aplicación del esfuerzo de flexión, la barra sufre una deformación, variando su geometría y curvándose alrededor de un centro, O.
Nombremos como R la distancia entre el centro y la posición de la fibra neutra, cuya longitud no hacambiado ya que es la única posición del perfil que no está sometida a tracciones o compresiones. La longitud inicial de la barra corresponde a la longitud del arco de circunferencia de radio R y ángulo θ.
Longitud de la fibra neutra
L = R \cdot \theta

Una fibra cualquiera del perfil puede identificarse por su distancia, y, respecto de la fibra neutra. Por criterio, se toman el sentido positivo hacia la zona de tracción, cuyas fibras han incrementado su longitud respecto de la longitud inicial de la barra, quedando el sentido negativo hacia la zona de compresión. La longitud de la fibra situada a una distancia y de la fibra neutra se obtiene como
L_2 = (R+y) \cdot \theta
Inicialmente, todas las fibras del perfil miden la misma longitud, esto es, la longitud inicial de la barra, L. La deformación, ε, de esta fibra causada por el esfuerzo de flexión pura se expresa como el incremento de longitud entre la longitud inicial y se trata de una deformación normal, perpendicular a la sección transversal de la barra.
\varepsilon = \dfrac{{\Delta L}}{L} = \dfrac{{{L_2} – L}}{L} = \dfrac{{\left( {R + y} \right) \cdot \theta – R \cdot \theta }}{{R \cdot \theta }} = \dfrac{y}{R}
En la zona elástica de un material, la relación entre la tensión normal y la deformación normal viene dada por la Ley de Hooke, a partir del módulo elástico, E. Sustituyendo la deformación producida por el esfuerzo de flexión en la Ley de Hooke, es posible obtener la tensión normal como función de la distancia y de la fibra analizada hasta la fibra neutra.
\sigma = E \cdot \varepsilon = \dfrac{{E \cdot y }}{R}
Sin embargo, la expresión anterior depende del radio, R, que es una consecuencia de la deformación producida. Resulta mucho más conveniente deducir una expresión que directamente dependa del momento flector aplicado.
Si cortamos la barra por una sección cualquiera, el equilibrio estático se consigue gracias a la distribución de la tensión normal a lo largo del perfil, que iguala el efecto del momento flector aplicado. Sobre cada elemento diferencial de la sección, es decir, cada trocito pequeño, situado a una distancia, y, de la fibra neutra, hay una tensión aplicada que genera un momento de giro contrario al momento aplicado. La suma de la contribución de todos los momentos en cada elemento diferencial es igual al momento aplicado, lo que se describe con una integral.
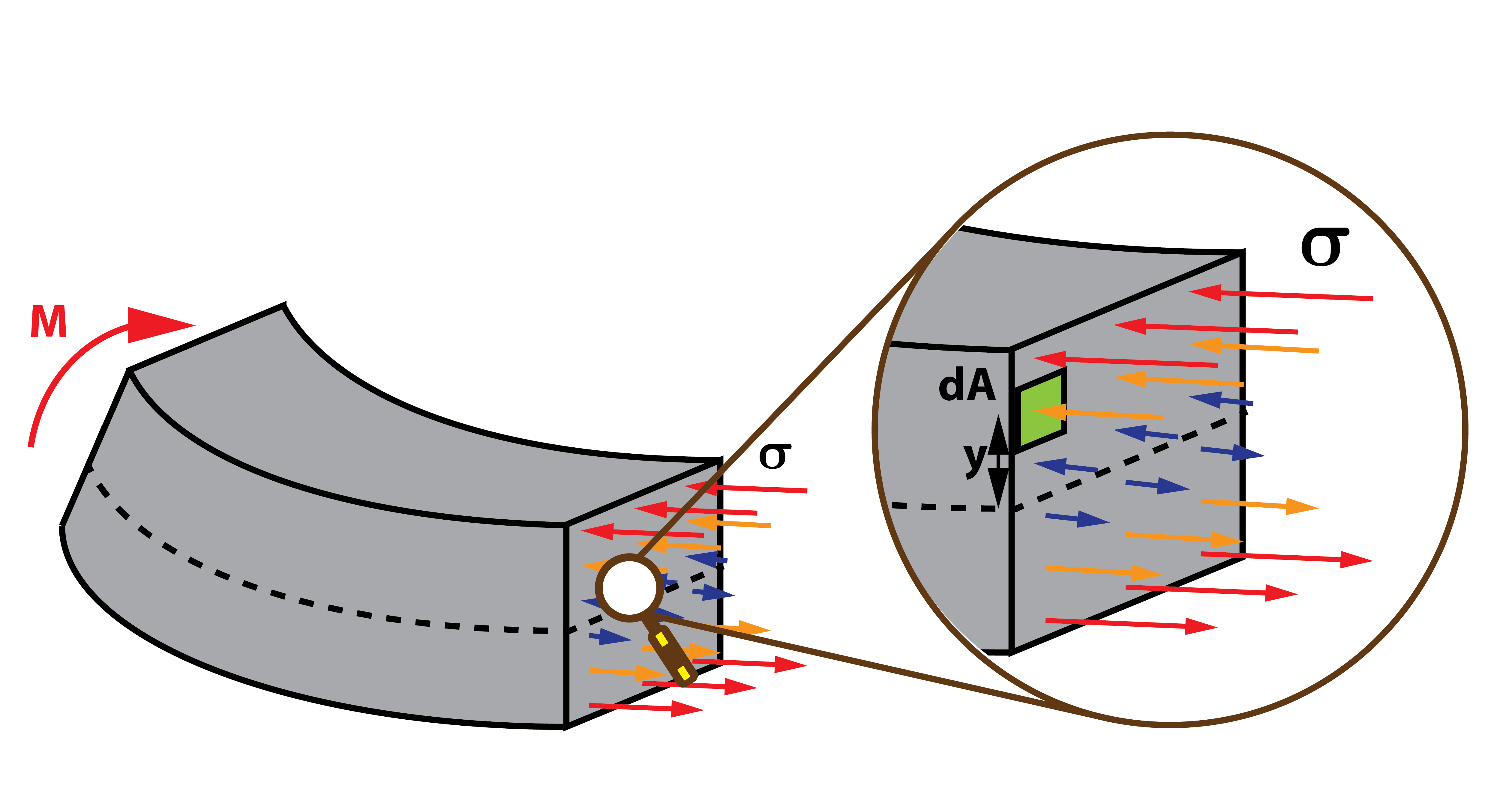
Balance de momentos
M = \int_s {\sigma \cdot y \cdot dA}
Resolviendo la integral, se obtiene una expresión que coincide con la definición de segundo momento de inercia, I, que es una propiedad geométrica del perfil.
M = \int_s {\sigma \cdot y \cdot dA} = \int_s {\dfrac{{E \cdot y}}{R} \cdot y \cdot dA} = \frac{E}{R}\int_s {{y^2} \cdot dA} = \dfrac{E}{R} \cdot I
Reemplazando la expresión de la tensión, σ, se deduce la tensión normal producida como función del momento, M, la posición, y, respecto de la fibra neutra y el segundo momento de inercia de la sección.
M = \dfrac{E}{R} \cdot I = \dfrac{\sigma }{y} \cdot I \to\sigma = \dfrac{{M \cdot y}}{I}
El signo de la tensión normal es positivo en la zona traccionada (valores y positivos) y negativo en la zona comprimida (valores y negativos). El valor máximo de la tensión, producida en las fibras exteriores se obtiene la distancia y máxima. De esta ecuación se deduce que el segundo momento de inercia de la sección tiene una importancia muy relevante en el comportamiento a flexión. Cuanto mayor sea el valor de I, mayor será la resistencia del perfil ante este tipo de esfuerzo, ya que, al estar dividiendo, la tensión normal generada es menor.

También se puede definir el módulo resistente elástico de la sección, W_y, como la división del momento de inercia entre la distancia a la fibra más externa. Así, la tensión máxima se obtiene directamente dividiendo el momento aplicado entre el módulo resistente.
Tanto los valores del segundo momento de inercia, I, y del módulo resistente, W_y, se encuentran recogidos en prontuarios para los tipos de perfil más comúnmente usados en estructuras.
Os animo a ver el siguiente vídeo donde se detallan todos estos conceptos con animaciones!!
