El esfuerzo de torsión es muy importante en ingeniería, ya que está presente en gran cantidad de mecanismos, como los sistemas de transmisión de los vehículos. También aparece en aerogeneradores, o en otras construcciones y aplicaciones de la vida real. En este artículo explicamos en qué consiste y las fórmulas principales para calcularlo. Además, encontrarás un vídeo explicativo con animaciones al final.
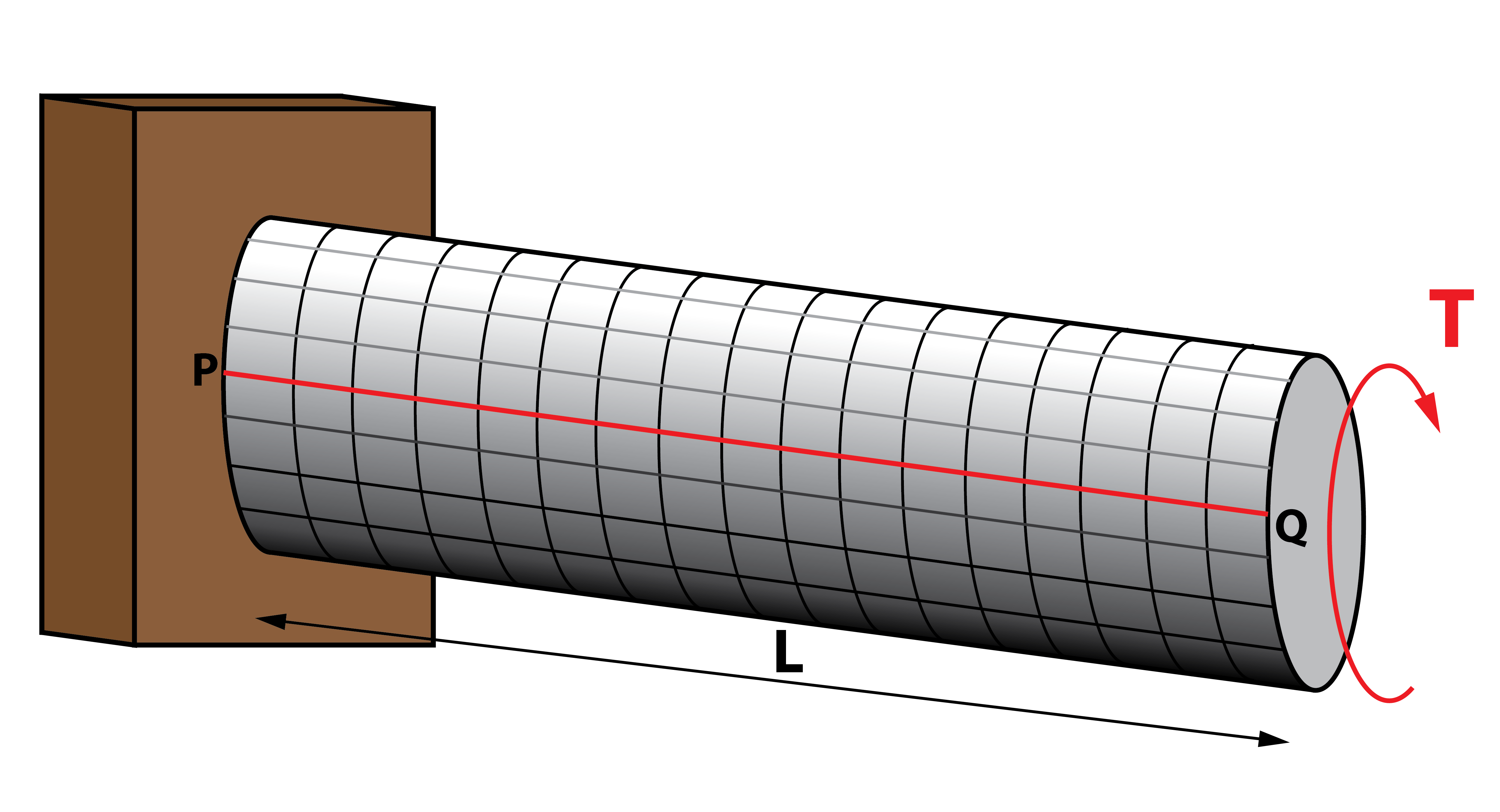
Fijémonos en esta barra de sección circular que tiene aplicada dos momentos de giro alrededor de su eje longitudinal, pero de sentido contrario en cada extremo. Estos momentos se conocen como momentos torsores, y generan que la barra se torsiones alrededor de su eje (que gire o se retuerza alrededor de éste). Gracias a la simetría circular del perfil, las distintas secciones de la barra giran sin cambiar su forma, únicamente rotan su posición.
Para poder tomar un extremo como referencia, analicemos una barra empotrada en su extremo izquierdo, con un torsor aplicado en el extremo derecho. Si dibujamos una línea que una dos puntos cualquiera P y Q, se observa cómo después de la torsión, Q varía su posición colocándose en Q’. Así se describe el ángulo de torsión, θ, que representa cuánto ha girado una sección concreta de la barra con respecto al estado inicial.
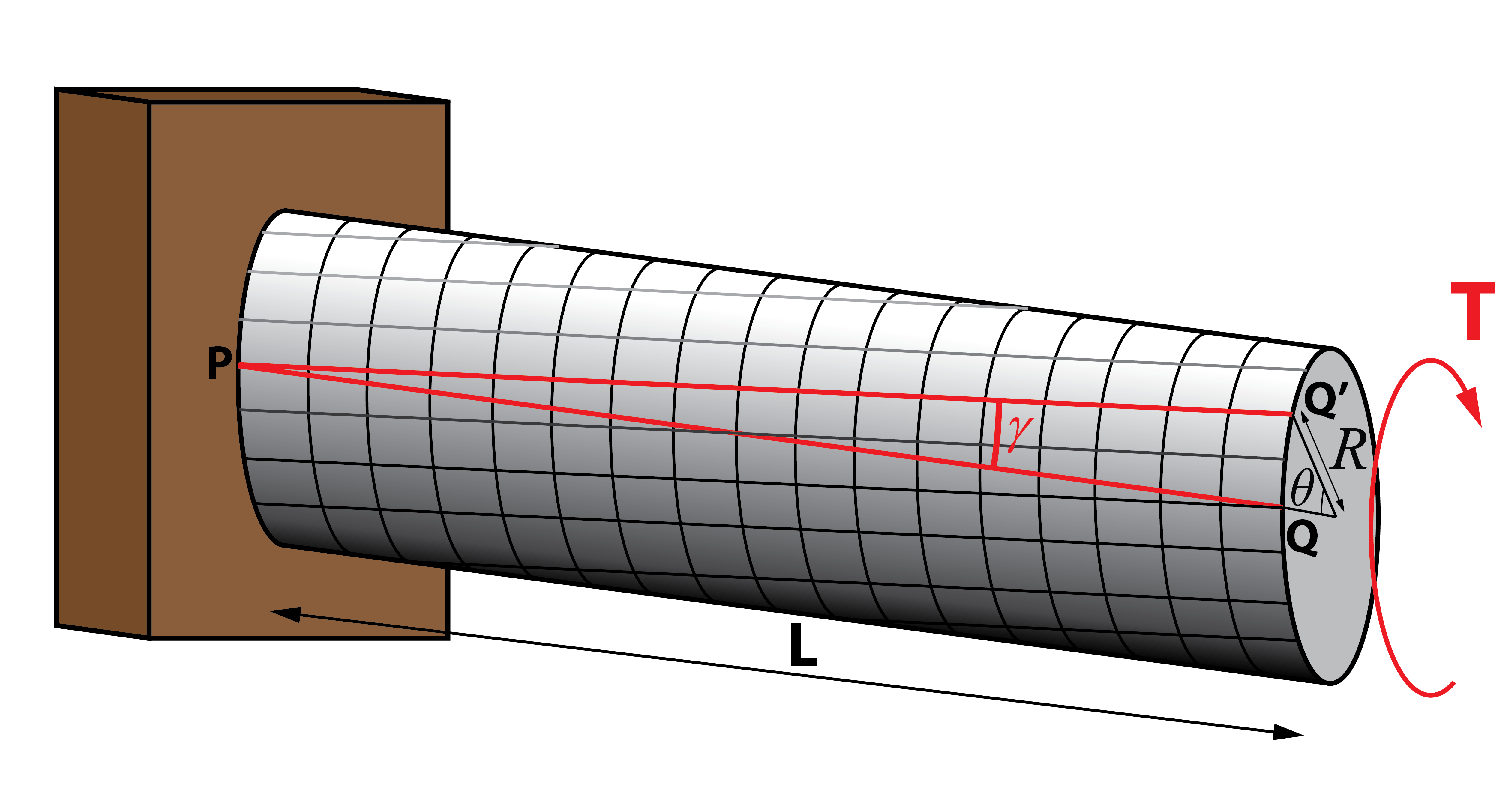
De esta manera, todos los elementos de la malla dibujada sobre la superficie de la barra habrán variado su geometría, produciéndose un deslizamiento relativo entre los lados izquierdo y derecho del cada elemento. Este tipo de deformación se denomina deformación cortante y queda definida por el ángulo γ.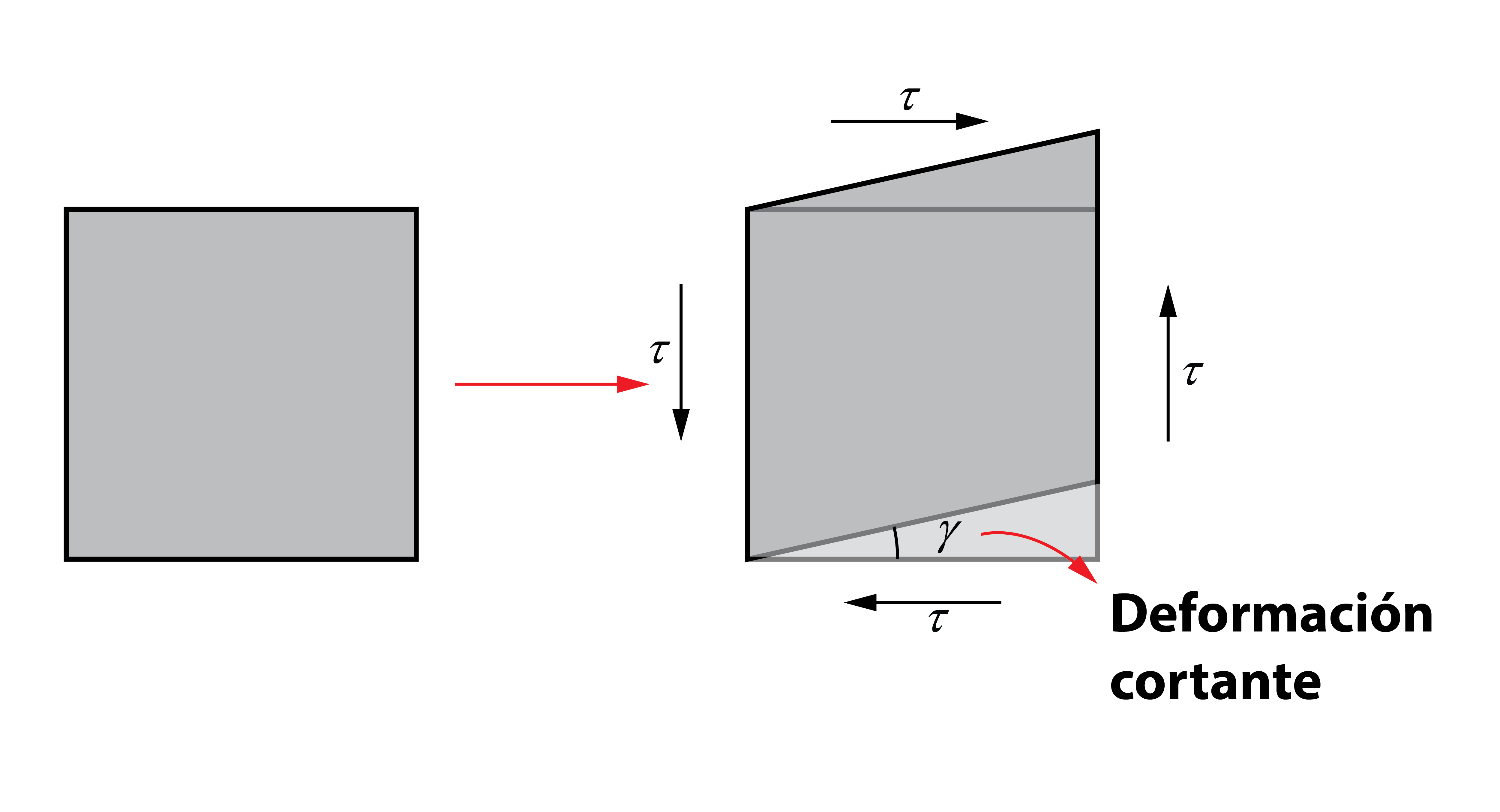
El valor del ángulo γ puede deducirse a partir de trigonometría. La tangente del ángulo es igual a la longitud del arco girado, QQ‘, entre la longitud de la barra PQ=L. Como γ es un ángulo pequeño (recuérdese que estas deducciones se realizan bajo la hipótesis de pequeñas deformaciones), podemos aproximarlo por el valor de su tangente.
\gamma = {\mathop{\rm tg}\nolimits} \gamma = \dfrac{{QQ'}}{{PQ}} = \dfrac{{R \cdot \theta }}{L}
Mediante la ecuación anterior, se calcula la deformación cortante máxima en la superficie exterior de la barra, definida por el radio R. En cualquier punto interior, la deformación cortante será menor, conforme disminuye el radio, siendo nula en la fibra central de la sección.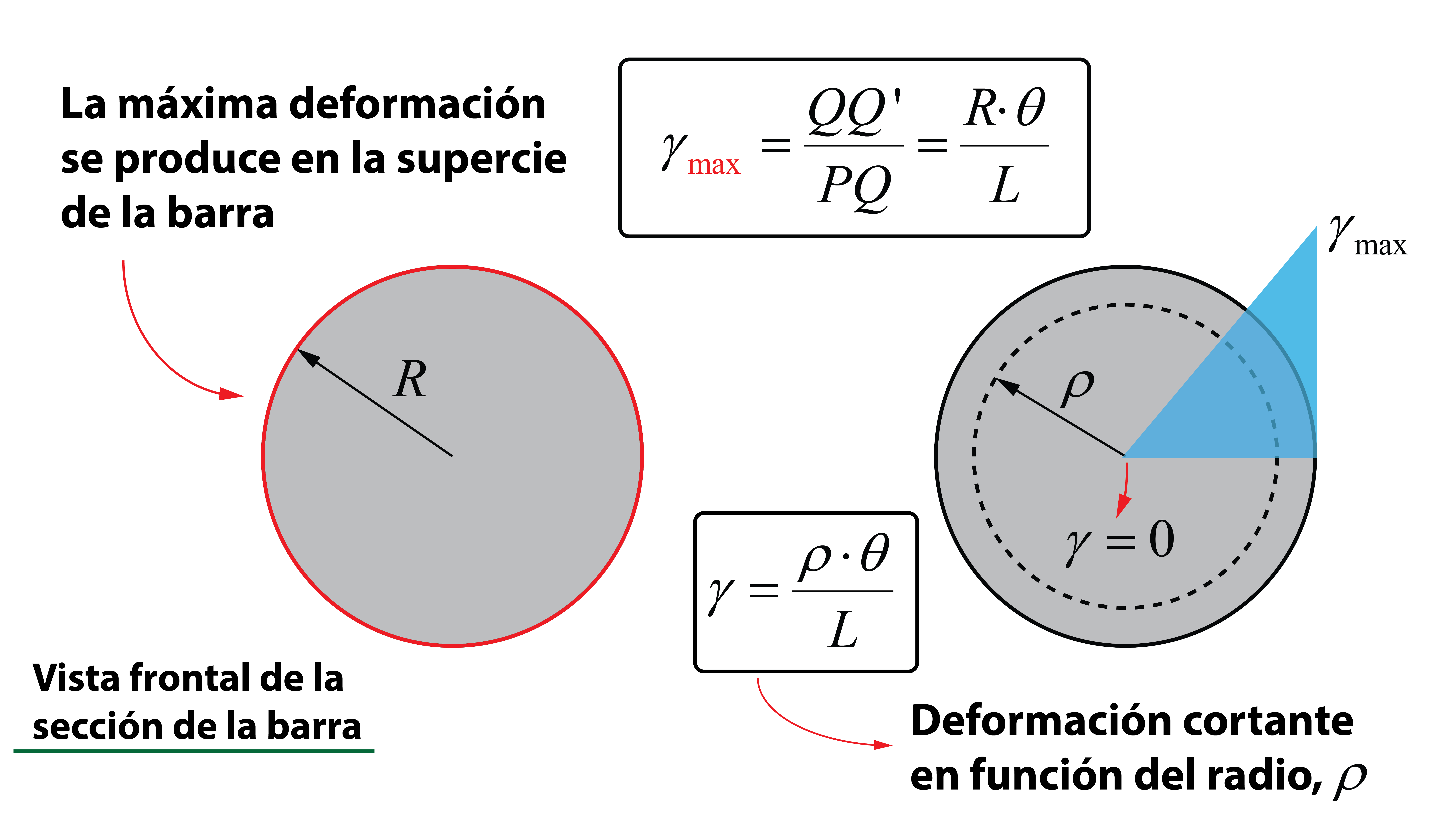
La deformación cortante vendrá acompañada de una tensión tangencial, τ (para más información sobre tensiones y deformaciones cortantes podéis ojear el artículo sobre el esfuerzo cortante). Para obtener una expresión que cuantifique el valor de la tensión tangencial en función del momento torsor aplicado, es necesario cortar la barra por una sección cualquiera para analizar qué ocurre internamente.
El momento torsor del extremo izquierdo debe estar equilibrado estáticamente. El equilibrio se consigue con la aparición de una tensión tangencial al plano e la sección de corte contraria al torsor. Sin embargo, la tensión tangencial no es constante en toda la sección, si no que sigue el mismo comportamiento que la deformación cortante. Es nula en el eje de la barra y crece linealmente hasta el valor máximo en la superficie externa.
La relación entre tensiones y deformaciones en la zona elástica de un material (aquella en la que la deformación es reversible tras el cese de aplicación de la carga) es lineal, y viene dada por la Ley de Hooke. Para el caso de esfuerzos tangenciales, la tensión tangencial, τ, es igual al módulo de elasticidad transversal, G, que es una propiedad del material, por la deformación tangencial, γ.
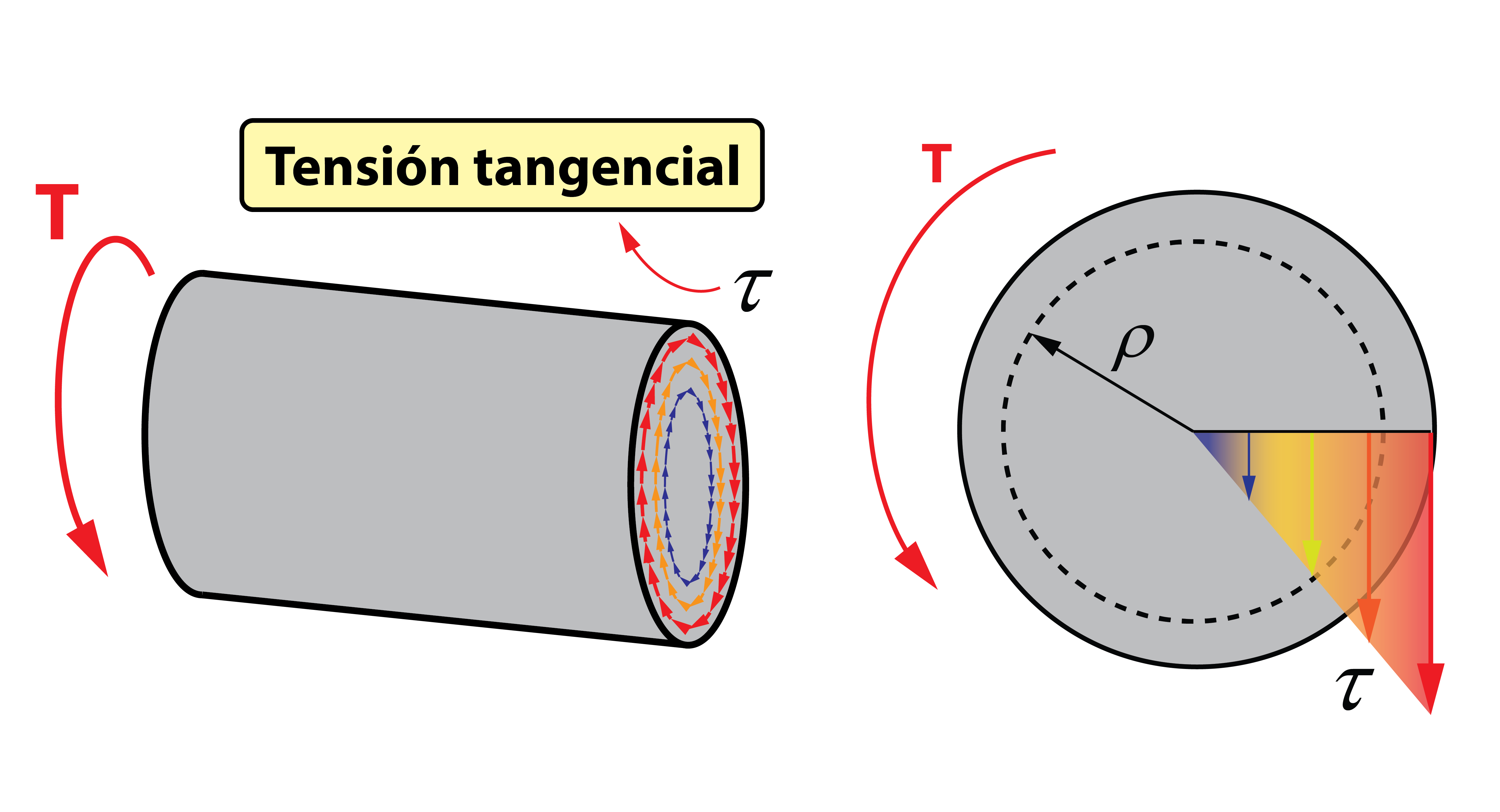
Tensión tangencial, τ, en función del radio, ρ
\tau = G \cdot \gamma = G \cdot \dfrac{{\rho \cdot \theta }}{L}
Aquí se explica como la tensión tangencial es creciente desde el centro al exterior de la barra, conforme se incrementa el valor del radio, ρ. Sin embargo, esta expresión no está directamente relacionada con el momento torsor aplicado.
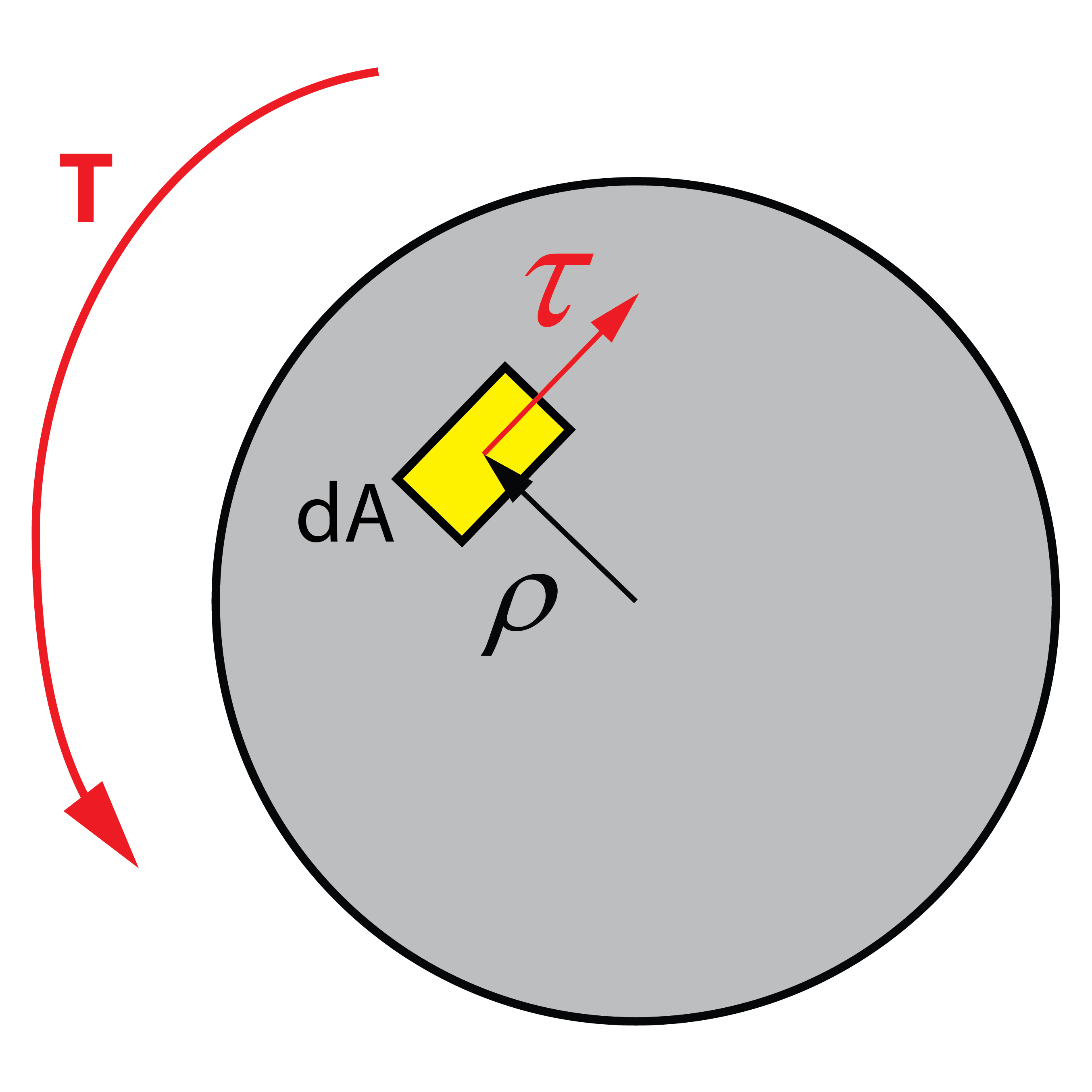
Para obtener esta relación, debemos fijarnos en un elemento diferencial cualquiera de la sección, situado a una distancia ρ del centro, sobre el que actúa una tensión tangencial, τ.
La suma de todas las tensiones tangenciales en cada elemento diferencial por su distancia ρ al centro será igual al momento torsor aplicado. Esto coincide con el concepto de integral.
El equilibrio estático se alcanza con la suma de los momentos torsores generados por la tensión tangencial aplicada en cada elemento diferencial
T = \sum {\tau \cdot \rho \cdot dA} \to T = \int_0^R {\tau \cdot \rho \cdot dA}
Sustituyendo la expresión de τ anteriormente deducida en función de la deformación cortante, y sacando fuera de la integral todos los términos constantes, se obtiene una expresión que coincide con la definición de momento polar de inercia de una sección, J. El momento polar es una propiedad geométrica relacionado con la resistencia de una sección ante un esfuerzo de torsión. Cuanto mayor sea este valor, mejor será el comportamiento de la sección.
T = \int_0^R {\tau \cdot \rho \cdot dA} = \int_0^R {G \cdot \dfrac{{\rho \cdot \theta }}{L} \cdot \rho \cdot dA} = \dfrac{{G \cdot \theta }}{L} \cdot \int_0^R {{\rho ^2} \cdot dA} \to T = \dfrac{{G \cdot \theta }}{L} \cdot J
Volviendo a utilizar la expresión de τ anterior, despejando y reordenando los términos, se obtiene el valor de la tensión tangencial en función del torsor aplicado, T, el radio, ρ, y el momento polar de inercia, J, así como el valor de la tensión tangencial máxima en la superficie de la barra.
\tau = \dfrac{{T \cdot \rho }}{J} \to {\tau _{\max }} = \dfrac{{T \cdot R}}{J}
Paralelamente, también se deduce la expresión del ángulo de torsión, θ.
\theta = \dfrac{{T \cdot L}}{{G \cdot J}}
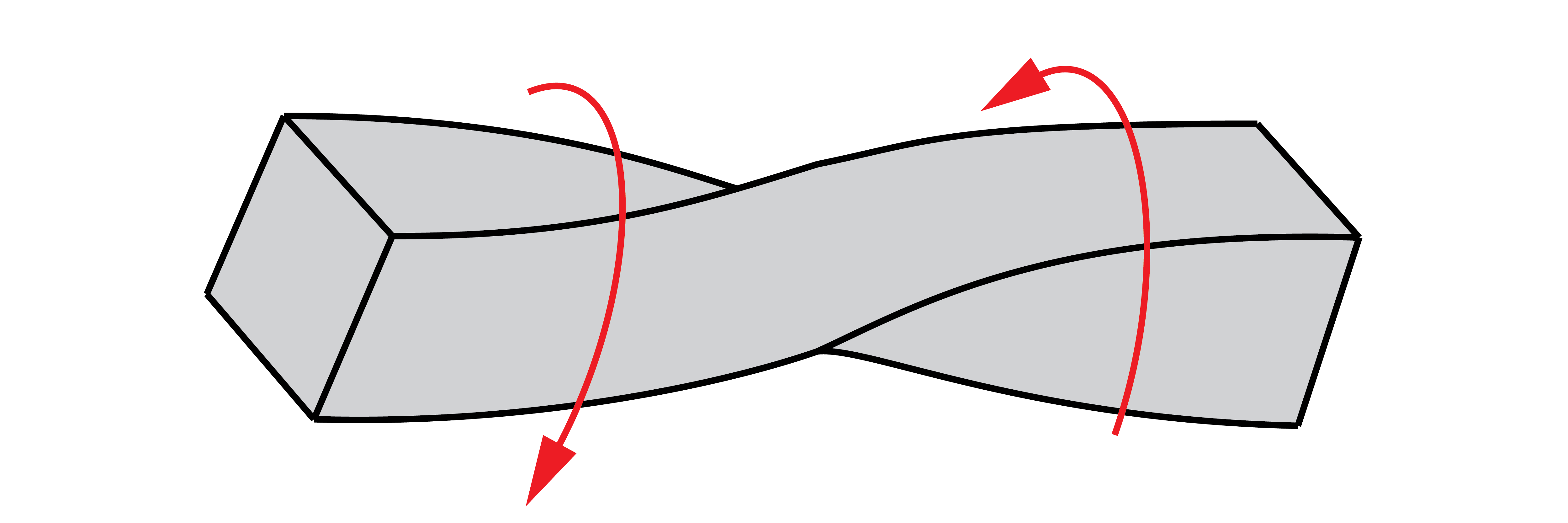
No obstante, estas deducciones matemáticas está limitadas a barras con geometría circular. En cualquier otro caso, el esfuerzo de torsión genera el alabeo de la barra, deformando las secciones, lo que complica los cálculos.
Os animo a ver el siguiente vídeo donde se detallan todos estos conceptos con animaciones!!