Cálculo de vigas y estructuras
Aprende cómo analizar los esfuerzos que hay en las vigas simples y estructuras industriales y las bases para su diseño

El cálculo de estructuras es una rama de la ingeniería de gran importancia, que engloba conocimientos de física, ciencia de los materiales, mecánica de materiales y medios continuos.
Aquí encontrarás una serie de artículos, ordenados por categorías, para aprender desde cero a calcular vigas isostáticas, vigas hiperestáticas, estructuras articuladas y pórticos.
También descubrirás el método para escoger el perfil de la viga válido en función de los esfuerzos y a evitar fenómenos de inestabilidad como el pandeo.
A continuación puedes escoger entre las distintas temáticas disponibles.
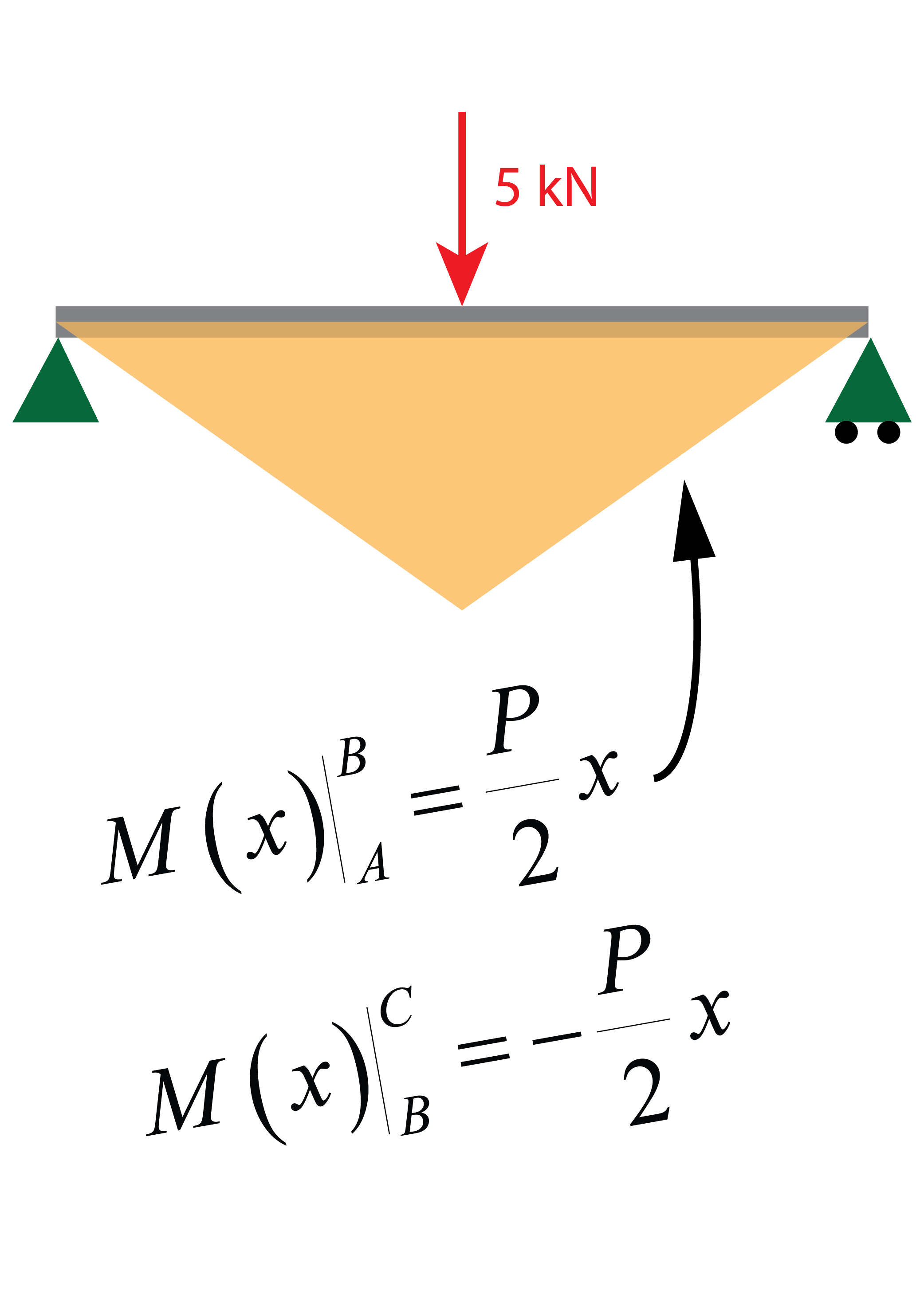
Cálculo de vigas, esfuerzos y leyes
Este es el primer paso en el análisis de vigas, aprender a obtener leyes de esfuerzo y dibujar los diagramas.
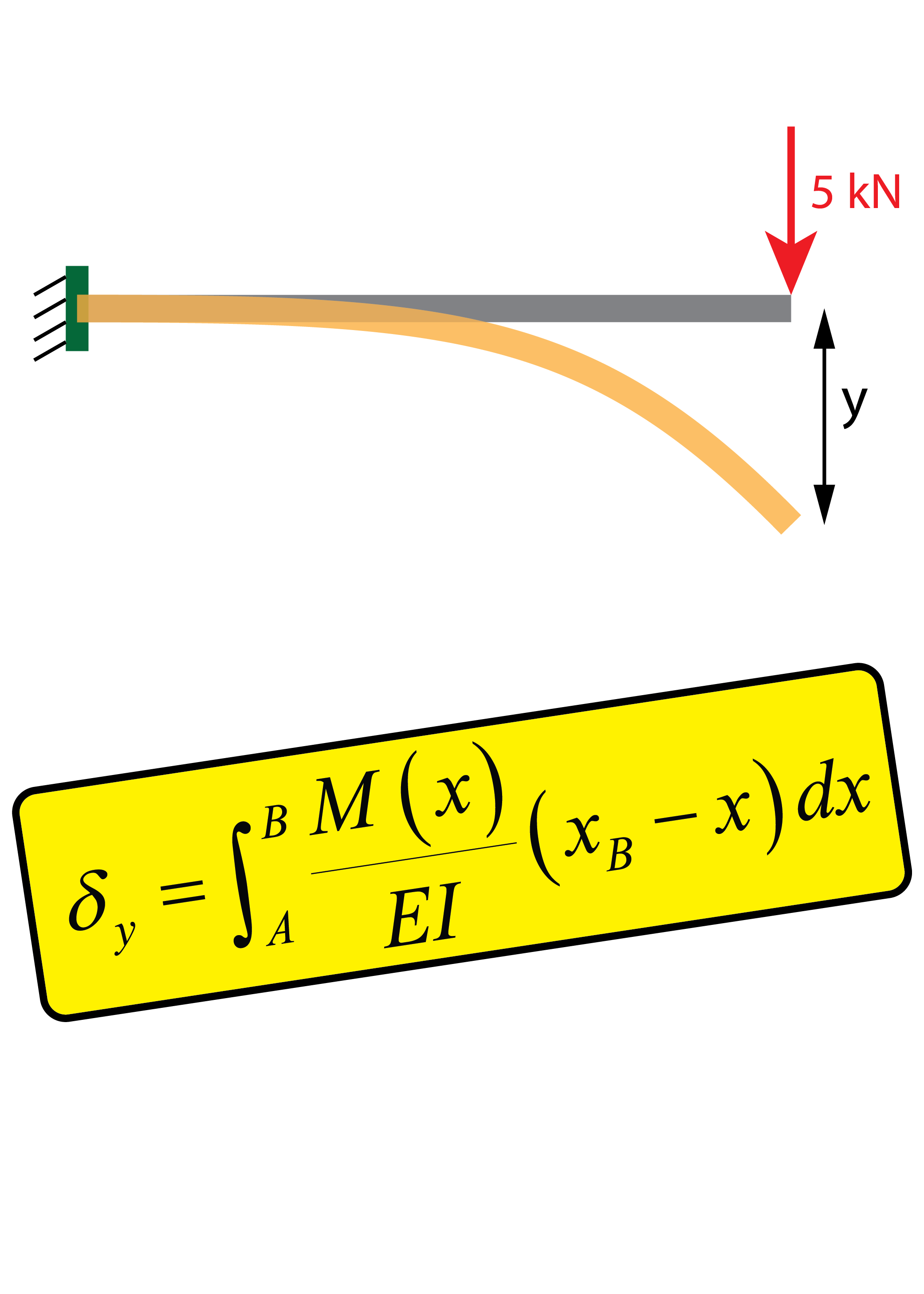
Deformaciones y giros
Aprende distintos métodos para calcular los desplazamientos y giros que hay en las vigas en función de los esfuerzos.
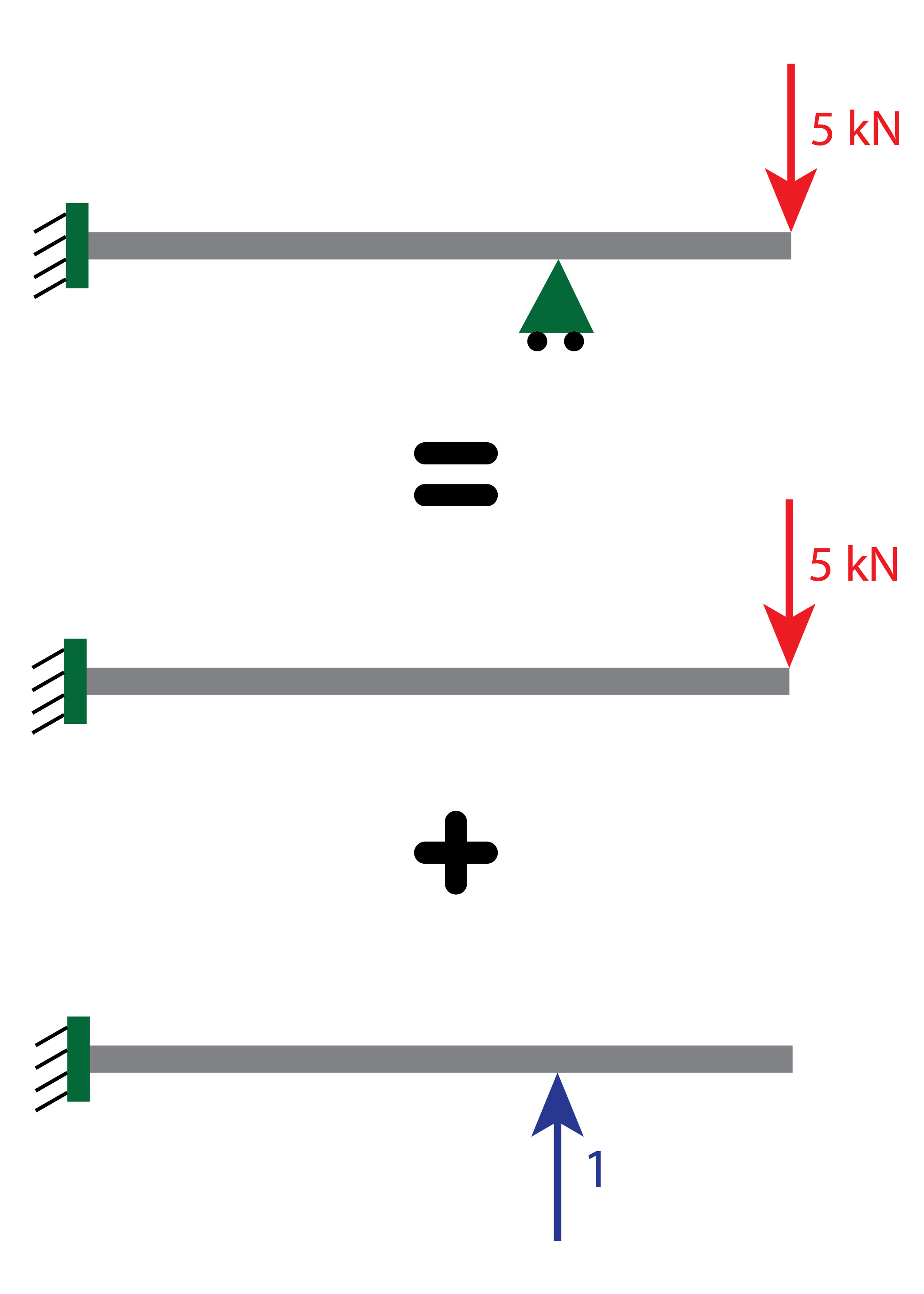
Vigas hiperestáticas
Si el número de restricciones aumentan, las cosas se complican. Aquí aprenderás como resolver las vigas más difíciles.
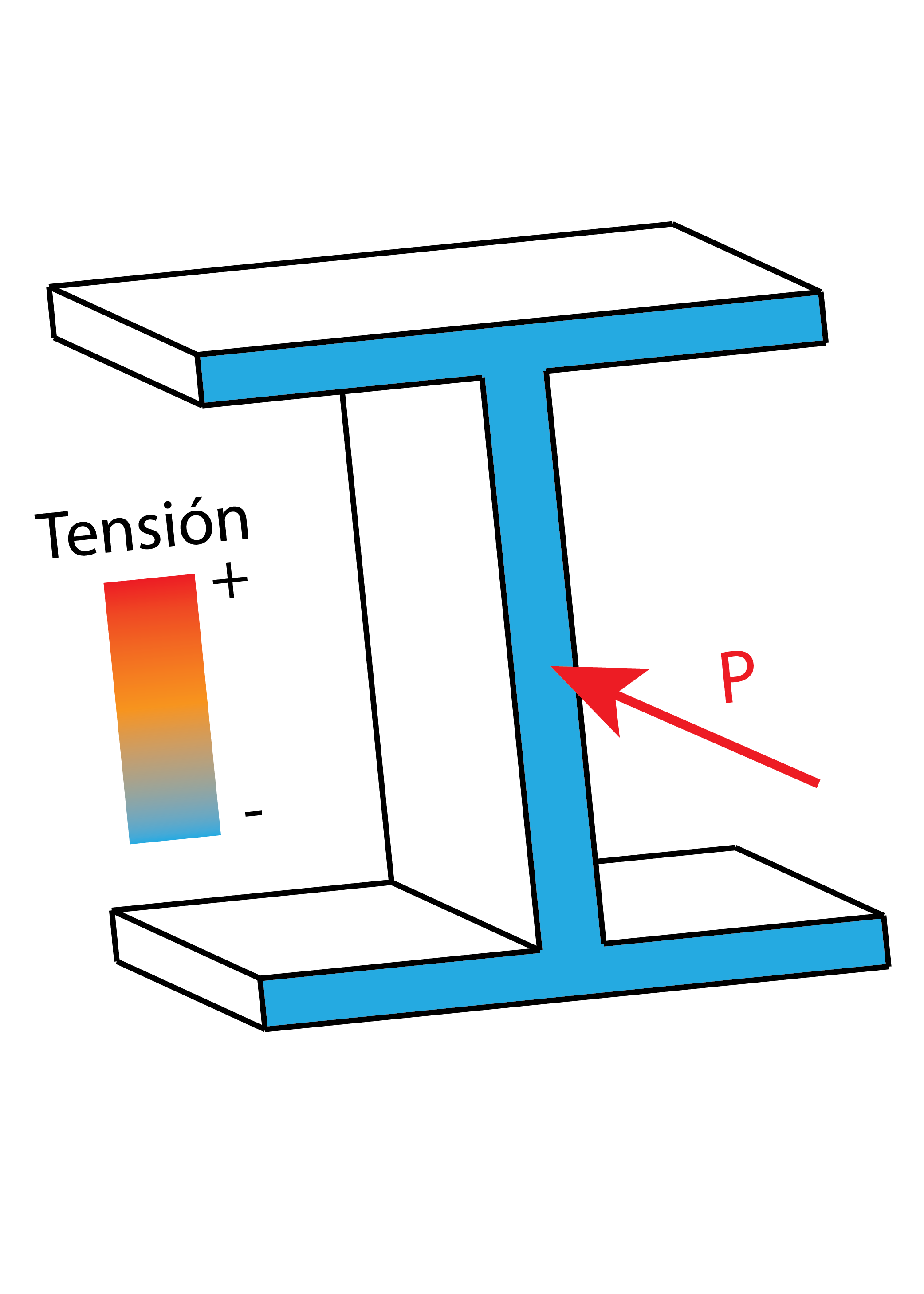
Dimensionamiento y diseño
¿Qué perfil debo escoger para mi viga? ¿Cómo se si resistirá sin romperse? De esto hablamos en esta sección.
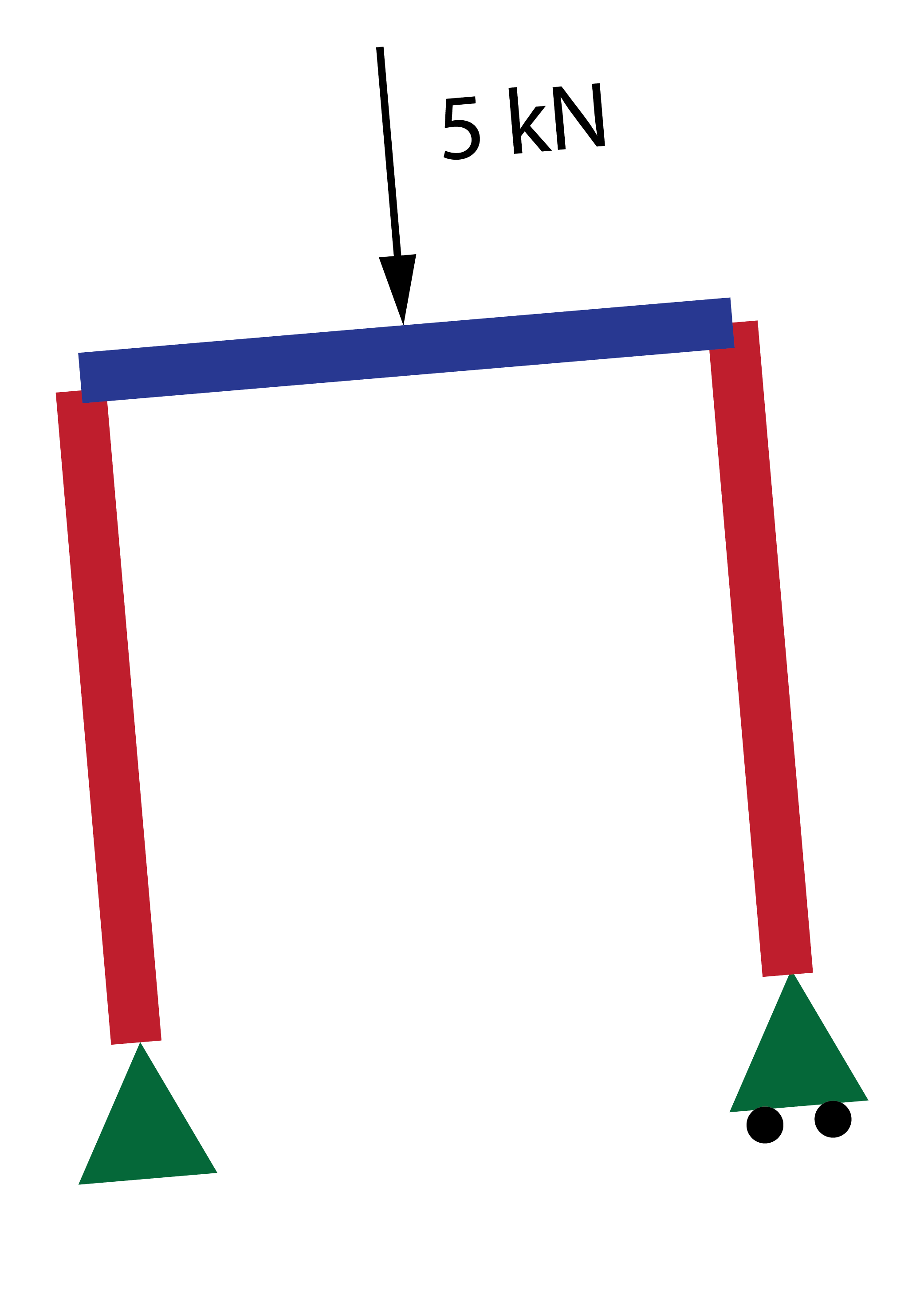
Cálculo de pórticos
Si ya sabes obtener leyes y diagramas de esfuerzos en vigas individuales, el siguiente paso es intentarlo con pórticos.
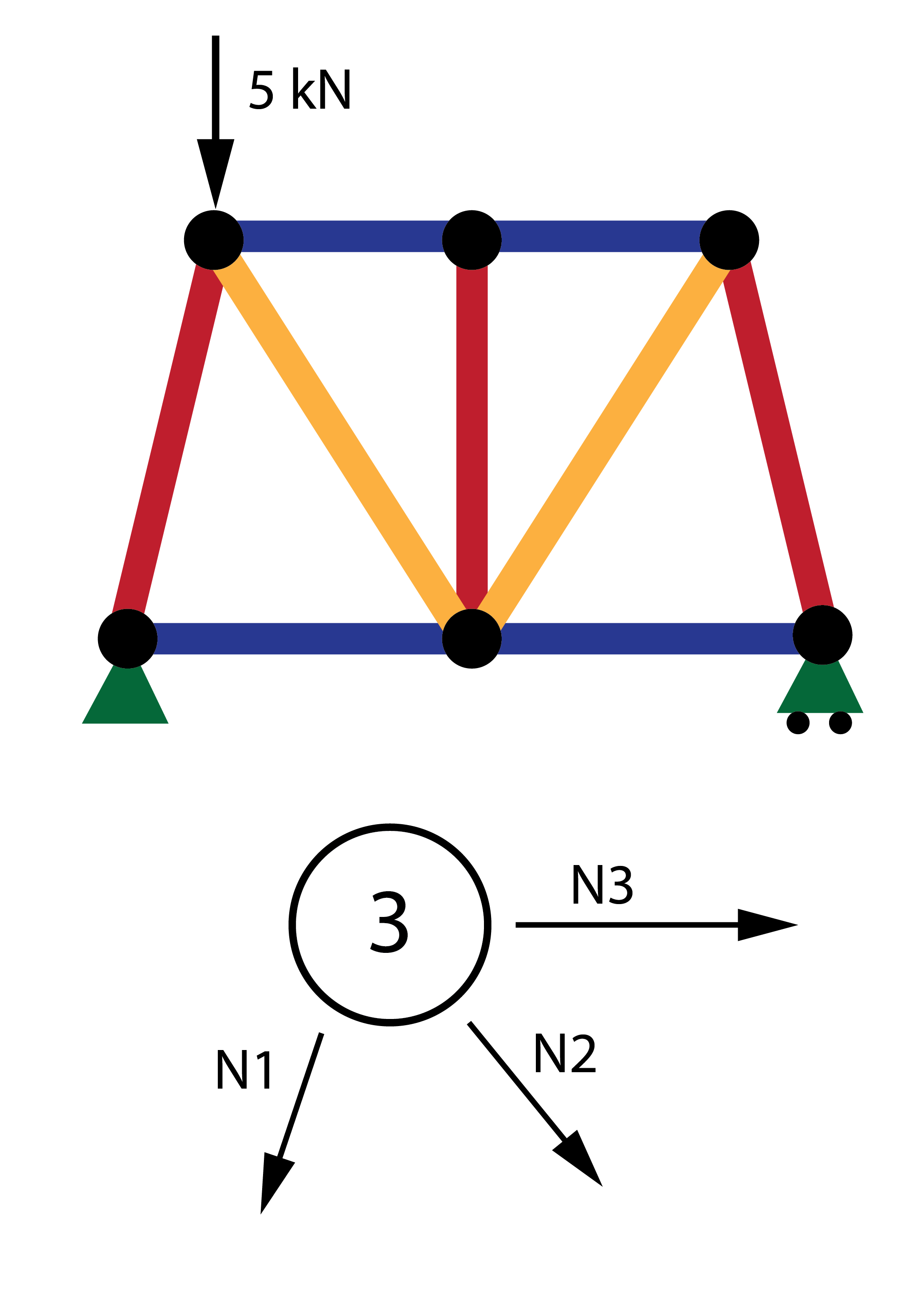
Estructuras articuladas
Las estructuras articuladas tienen unos métodos de cálculo específicos. Aquí aprenderás como analizarlas.
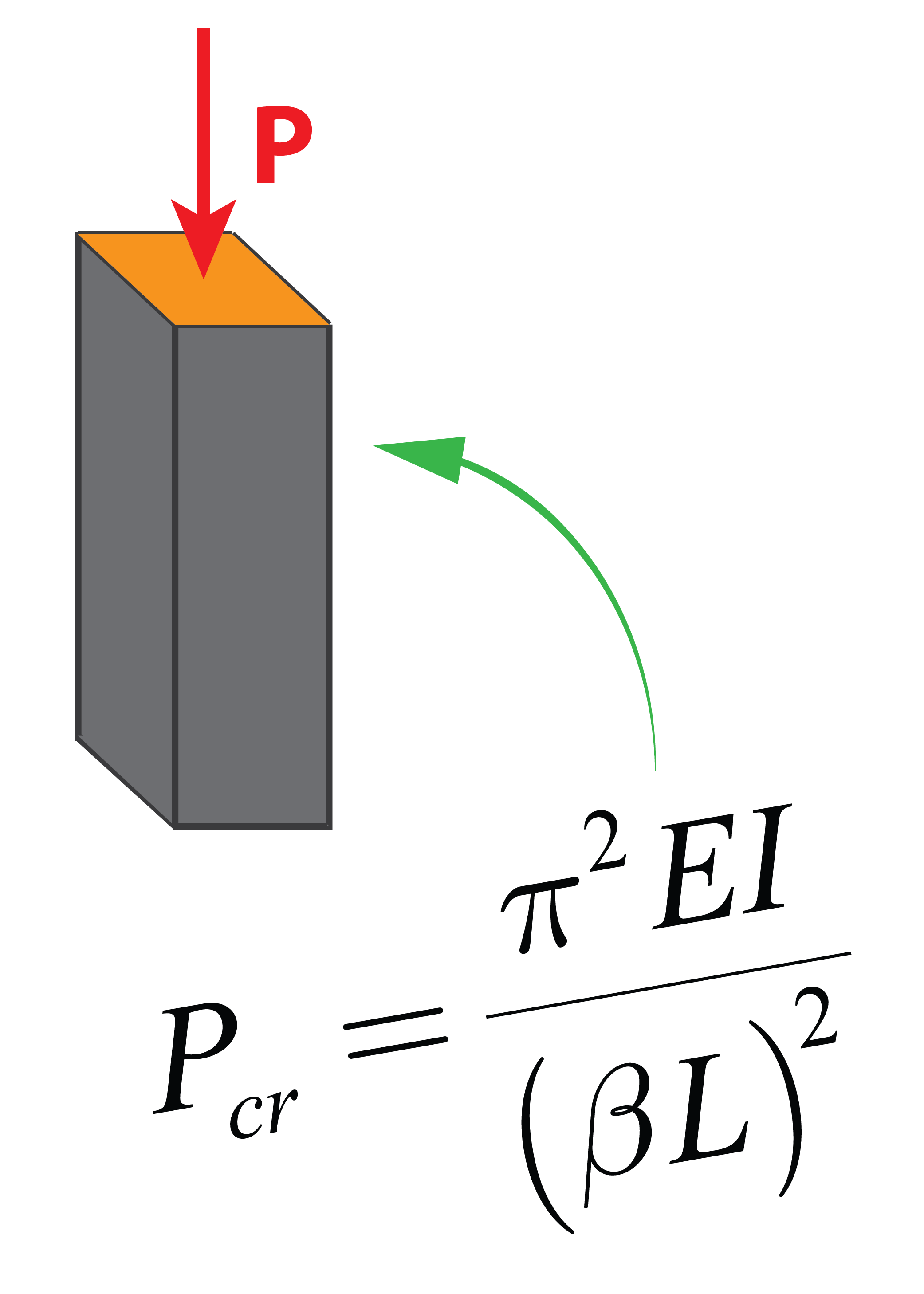
Construcciones industriales
Aquí aprenderás otros conceptos relacionados con las estructuras, como el diseño de arriostramientos contra pandeo y pandeo lateral.
Puedes profundizar en la aplicación de estos conceptos básicos con cada uno de los siguientes artículos avanzados.
Esfuerzos combinados
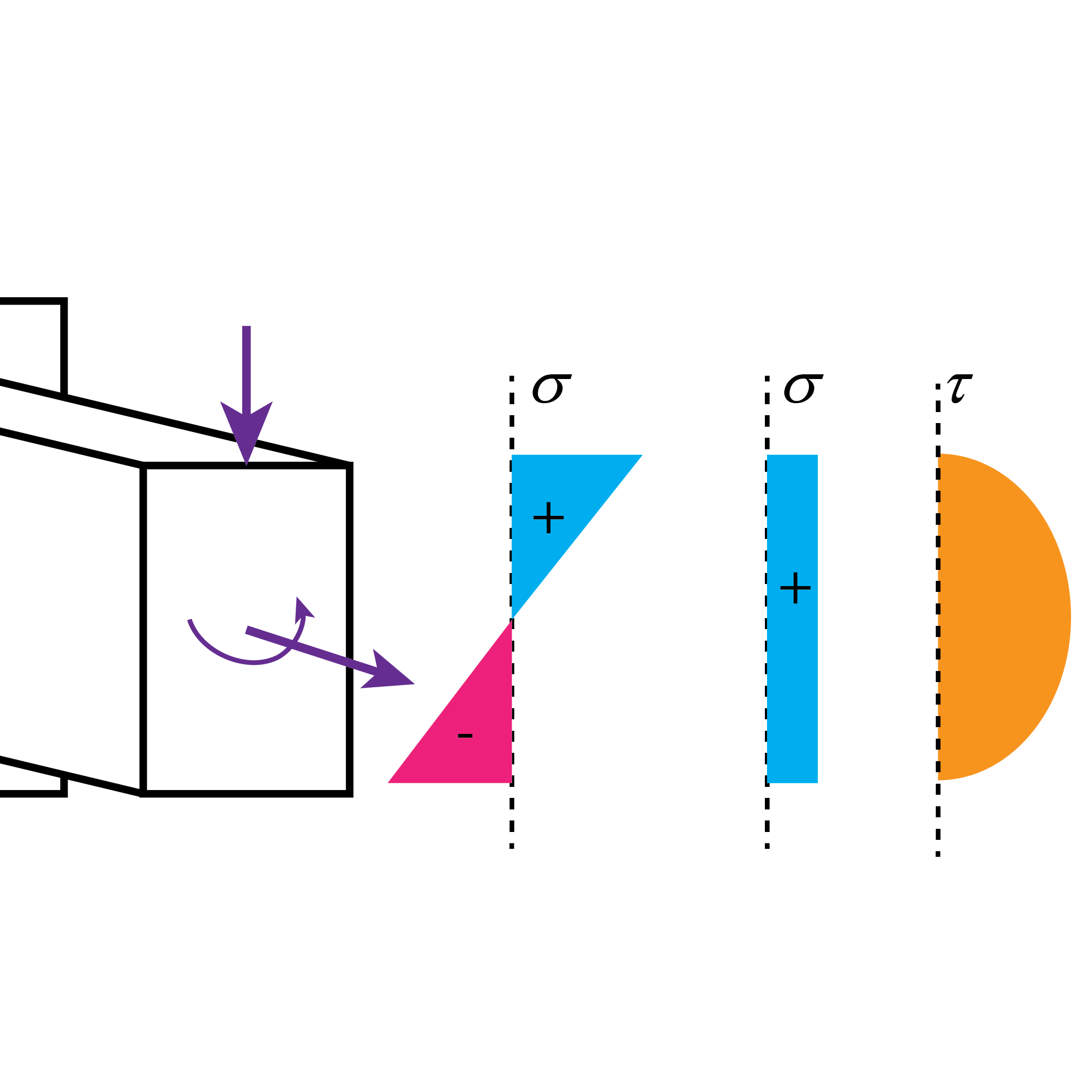
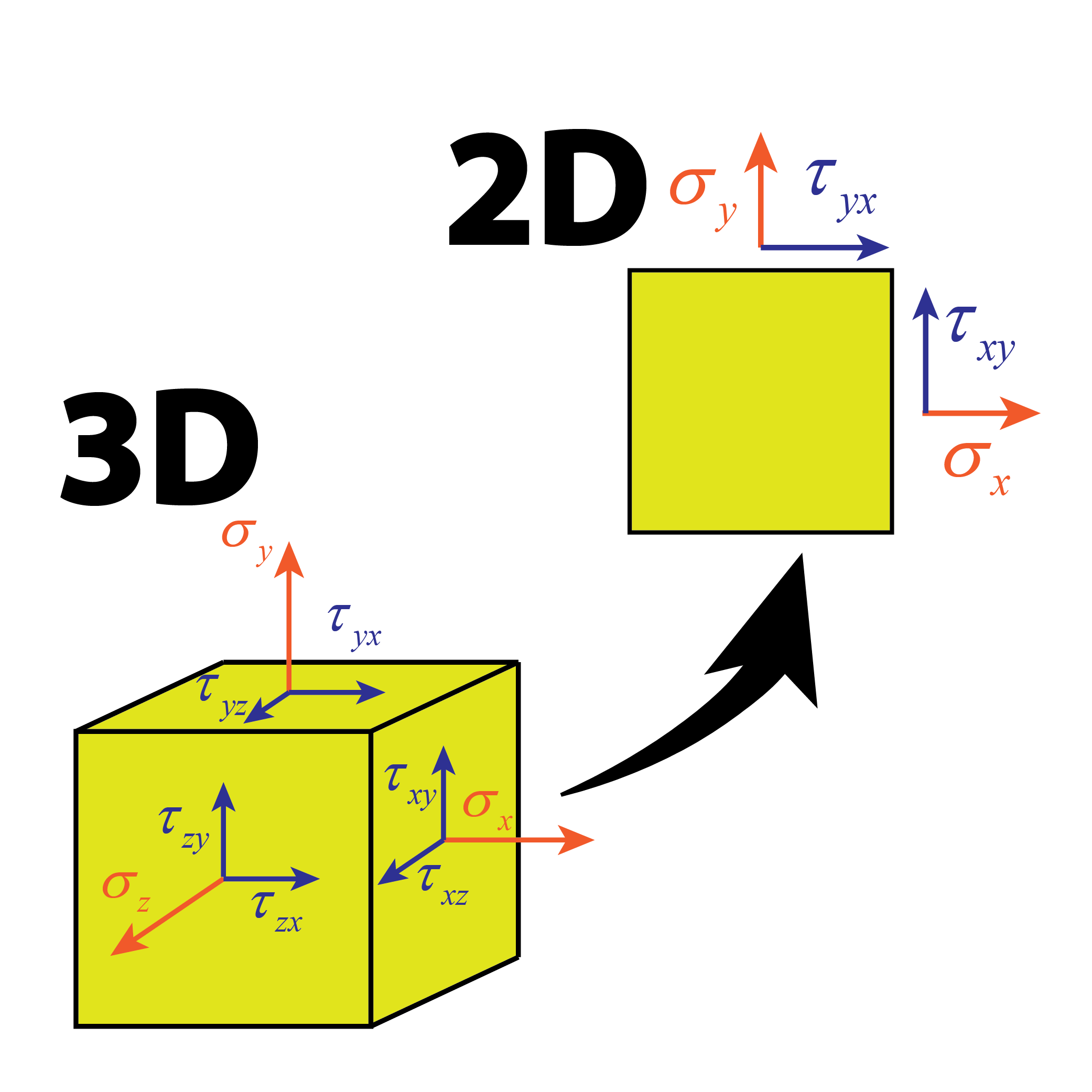
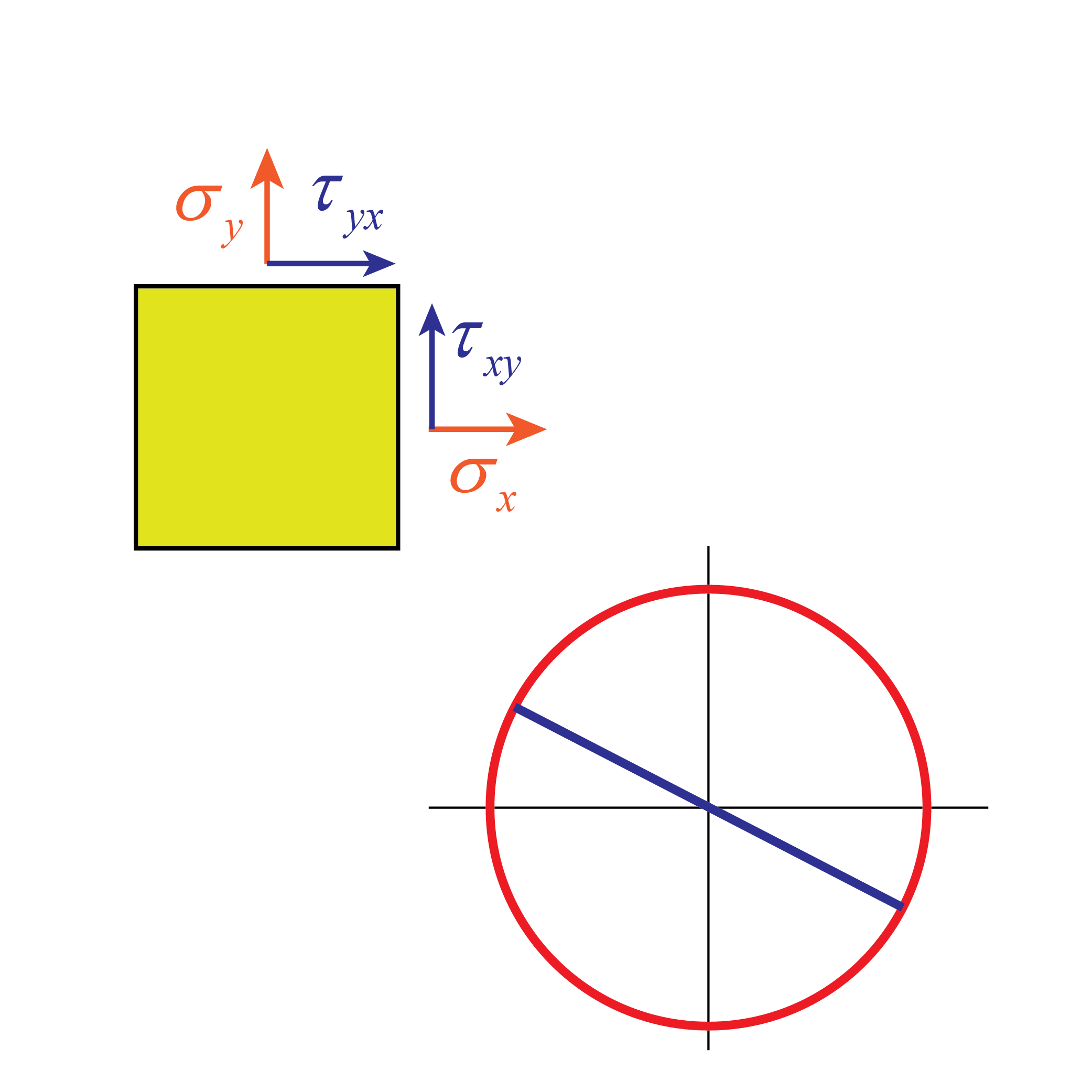
Tensor de tensiones
Aprende qué es el tensor de tensiones, cómo obtener tensiones y direcciones principales y cómo representar los círculos de Mohr.
Tensión y deformación plana
Si la geometría del sólido y la aplicación de las cargas lo permiten, la simplificaciones de tensión plana y deformación plana son muy útiles.