Los esfuerzos de tracción y compresión están presentes en la mayoría de piezas, objetos y estructuras que encontramos a nuestro alrededor. En este artículo explicamos en qué consisten, cómo se generan y cómo se estudian en ingeniería. También tenemos un vídeo al final del artículo.
En mecánica de materiales, se denomina Tracción al esfuerzo interno al que se somete un cuerpo cuando son aplicadas dos fuerzas que actúan en sentidos opuestos. Estas dos cargas tienen a estirar el cuerpo, es decir, a alargar su longitud en la dirección de aplicación de las cargas.
El esfuerzo de Compresión implica el escenario opuesto. Las dos fuerzas aplicadas tienden a acortar la longitud del cuerpo.
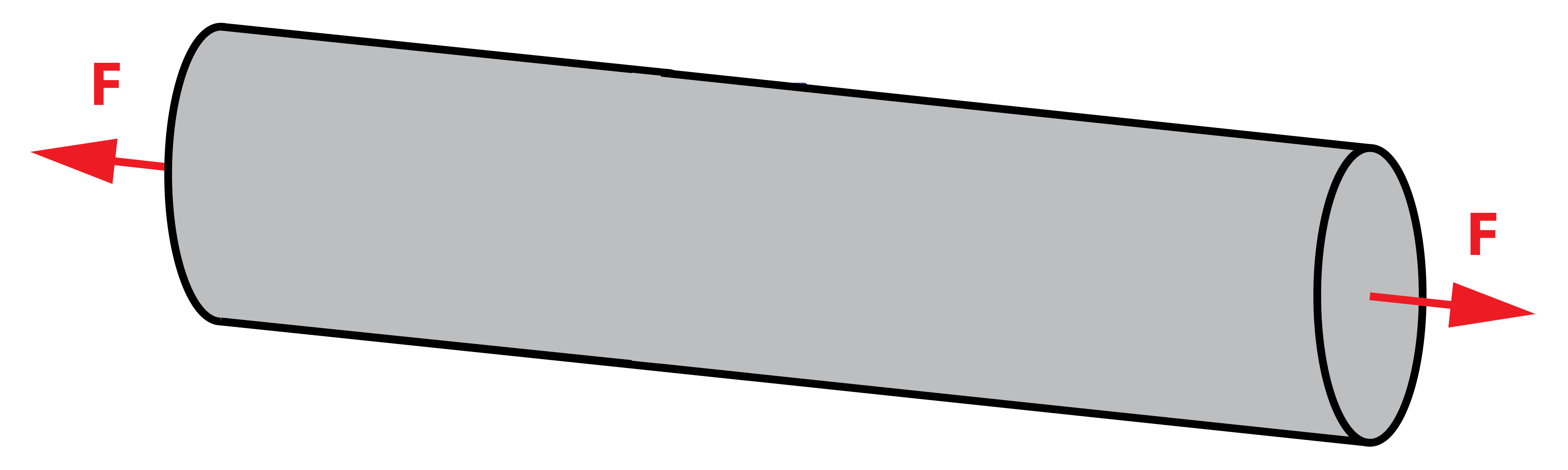
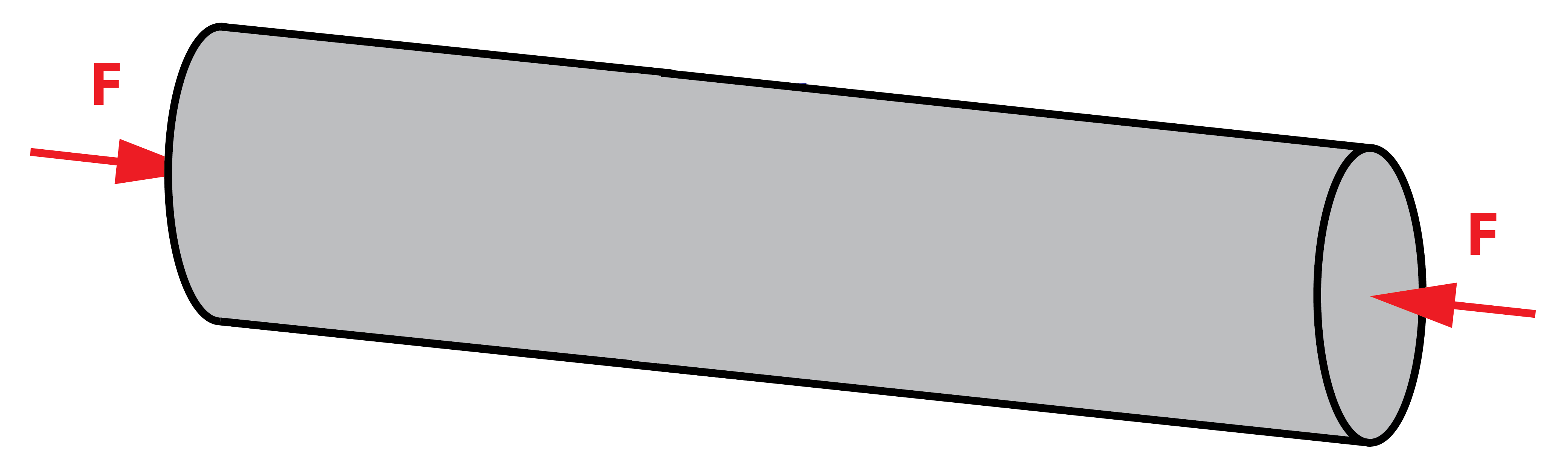
En ambos casos, el sólido se encuentra bajo carga uniaxial ya que las fuerzas únicamente están aplicadas en una dirección, en este caso coincidente con su eje longitudinal. En el interior del sólido, como resultado de las cargas aplicadas aparece una tensión interna.
Recordatorio: Tensiones y deformaciones
Como resultado de la aplicación de cargas, los sólidos sufren tensiones internas y deformaciones. Estos son dos conceptos básicos en mecánica de materiales que describen como los sólidos responden ante la aplicación de las cargas y que son necesarios entender previamente.
- La Tensión (o esfuerzo interno) es una magnitud física que mide la reacción que se produce en el interior de una pieza debido a las cargas que están aplicadas sobre él. Tiene unidades de fuerza partido de superficie, \dfrac{N}{m^2}, siendo un concepto físico necesario para relacionar fuerzas aplicadas en una pieza, con las propiedades resistentes del material y su geometría. Existen dos tipos de tensiones: normales, si son perpendiculares a la superficie y tensiones tangenciales, paralelas a la superficie.
- La Deformación es una medida de los desplazamientos que ocurren en el interior del sólido como resultado de las cargas aplicadas. Existen deformaciones normales y deformaciones tangenciales.
Para entender el concepto de tensión interna, es necesario cortar el sólido (la barra) por una sección cualquiera. Inicialmente, la barra está en equilibrio. Ambas fuerzas tienen la misma magnitud en sentidos opuestos, siendo el sumatorio de fuerzas nulo.
Después del corte (imaginario), la barra debe continuar en equilibrio. Aquí es donde surge el concepto de tensión interna, asociada al plano de corte. Como la tensión es perpendicular al plano, se conoce como tensión normal.
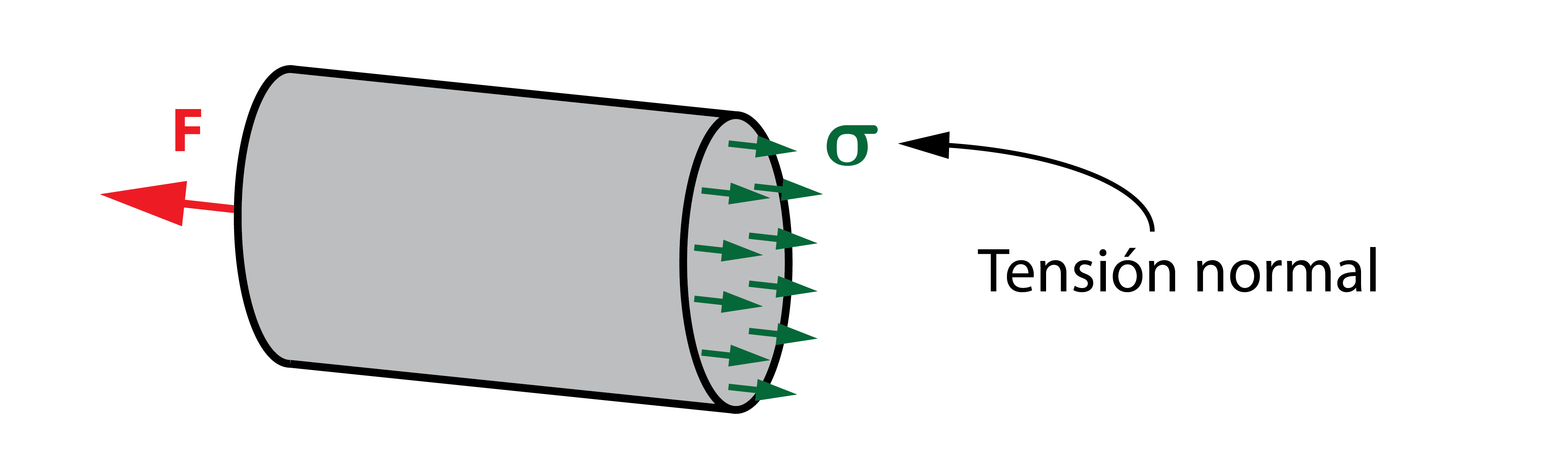
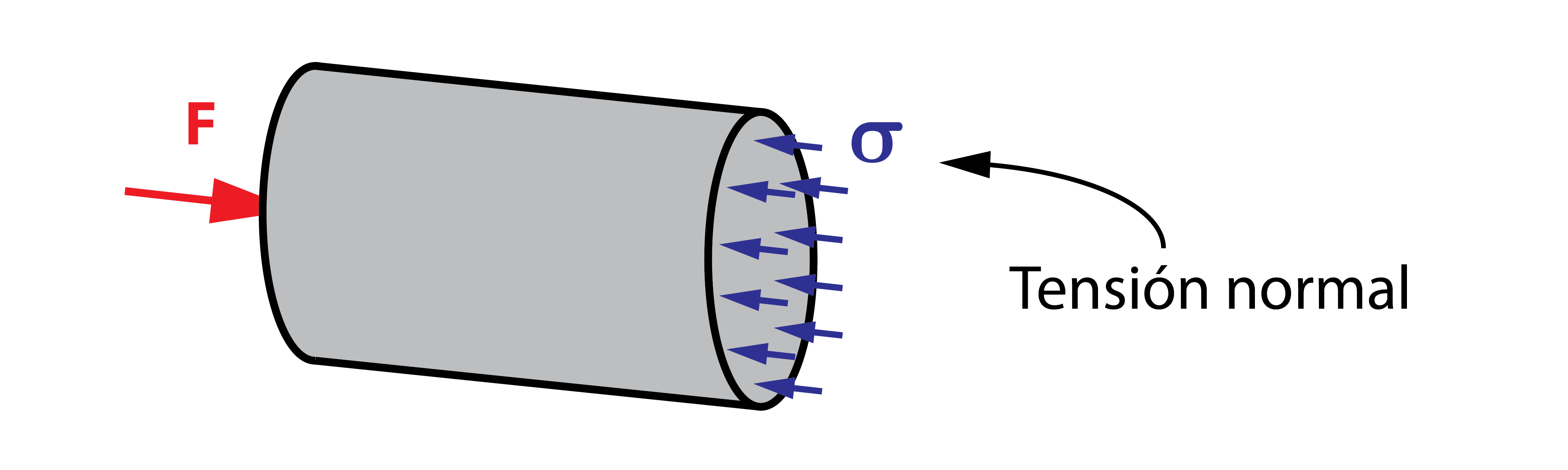
El efecto que produce esta tensión en la sección transversal es igual a la carga aplicada. Por lo tanto, la tensión normal por el área de la sección de la barra es igual a la fuerza aplicada. Despejando, se concluye que la tensión interna generada en la barra es igual a la fuerza aplicada entre el área transversal, quedando uniformemente distribuida por toda la sección.
\sum {\overrightarrow F } = 0
F = \sigma \cdot A
\sigma = \dfrac{F}{A}
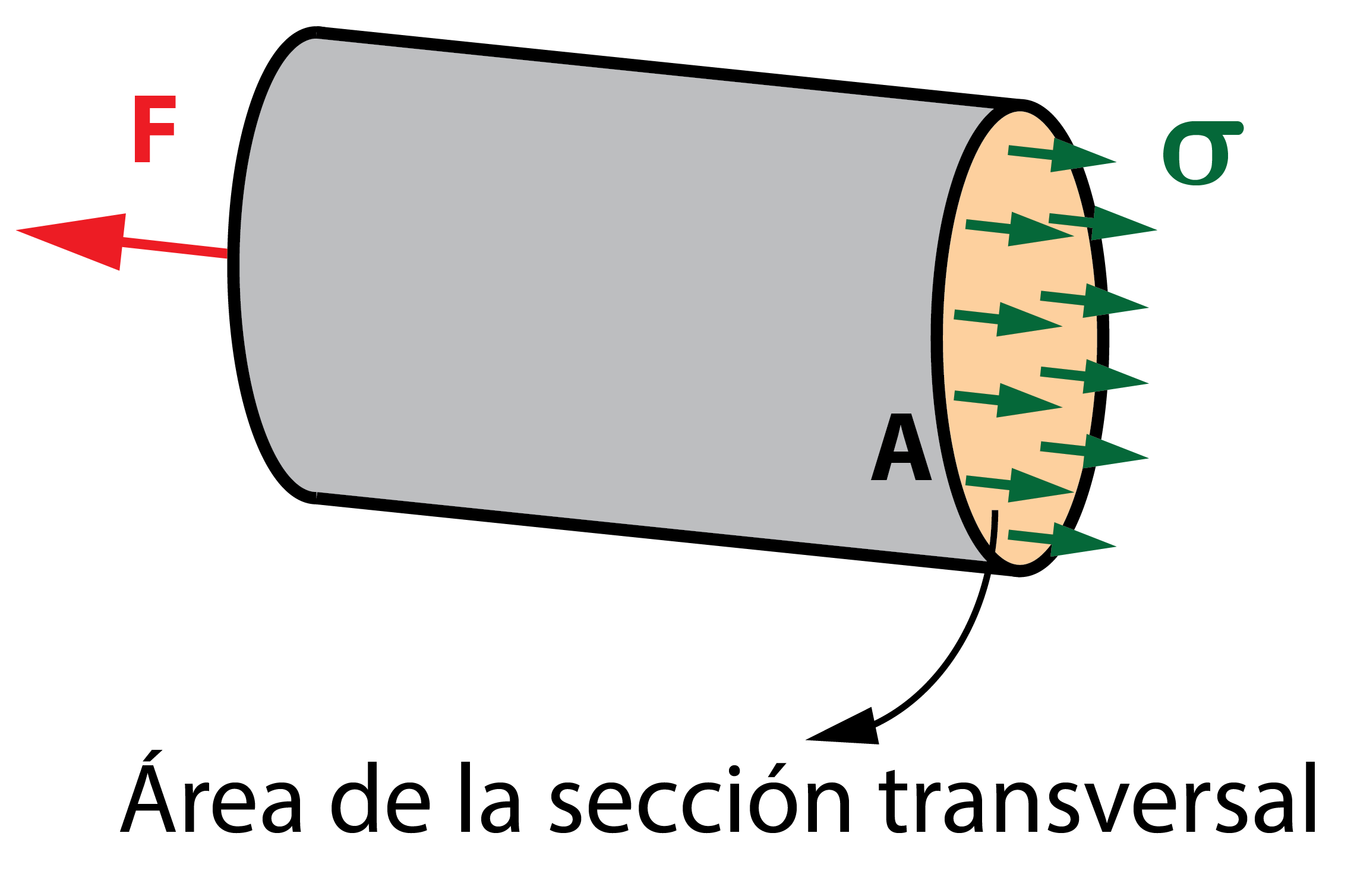
La tensión normal generada debido al esfuerzo de tracción es definida, por criterio, como positiva. Cuando el esfuerzo es de compresión, la tensión normal tiene signo negativo. Puede comprobarse gráficamente en la figura como el sentido de las flechas que representan la tensión es contrario en ambos casos.
¿Por qué la tensión es más importante que la fuerza aplicada?
Desde el punto de vista de la ingeniería y la mecánica de materiales, el concepto de tensión es más interesante que el propio valor de la fuerza.
Lógicamente, si la barra que es traccionada o comprimida es más gruesa, soportará una carga o fuerza mayor que una que sea más delgada. Es decir, la fuerza máxima que la pieza puede resistir depende del área de su sección transversal.
Sin embargo, la tensión límite que soporta la barra depende únicamente del material y sus propiedades. Conociendo las propiedades del material, a partir de los datos obtenidos del Ensayo de Tracción, es posible predecir qué carga máxima se puede aplicar en la pieza para que no se deforme plásticamente o incluso llegue a la rotura. Alternativamente, también es posible diseñar qué sección resistente requiere la pieza si se conoce la carga máxima que debe soportar.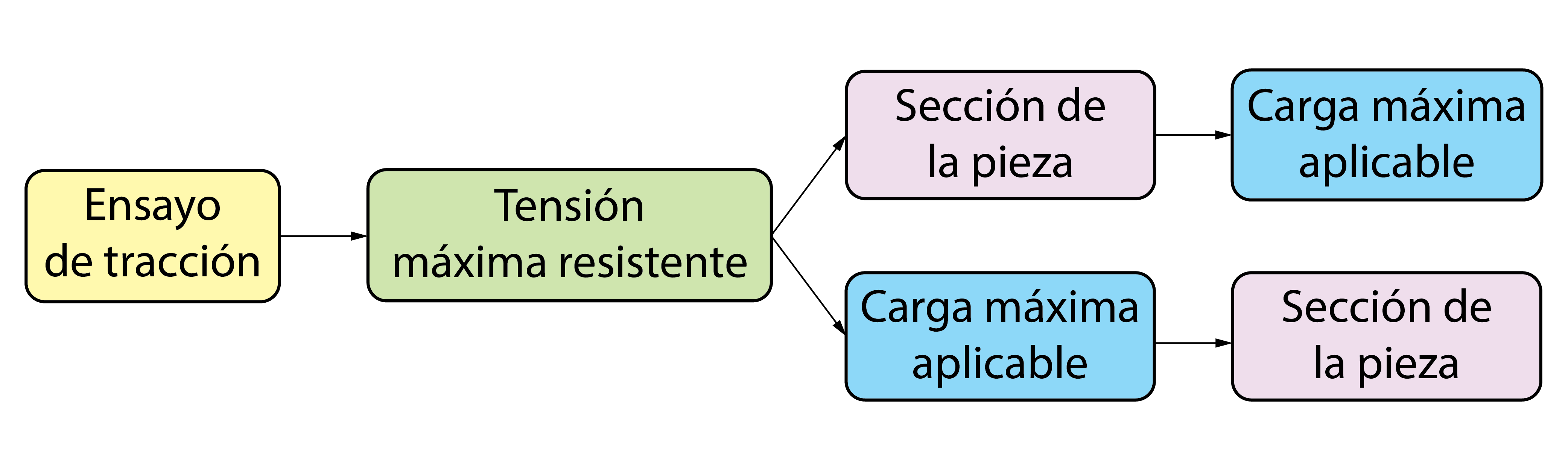
Además de la tensión normal producida en la barra, los esfuerzos de tracción y compresión generan una deformación en el sólido. Esta deformación se define como la variación de longitud en la barra, dividida entre la longitud inicial. El resultado es un número adimensional que representa el porcentaje de variación de longitud.
Definición de deformación
\varepsilon = \dfrac{{\Delta L}}{L}
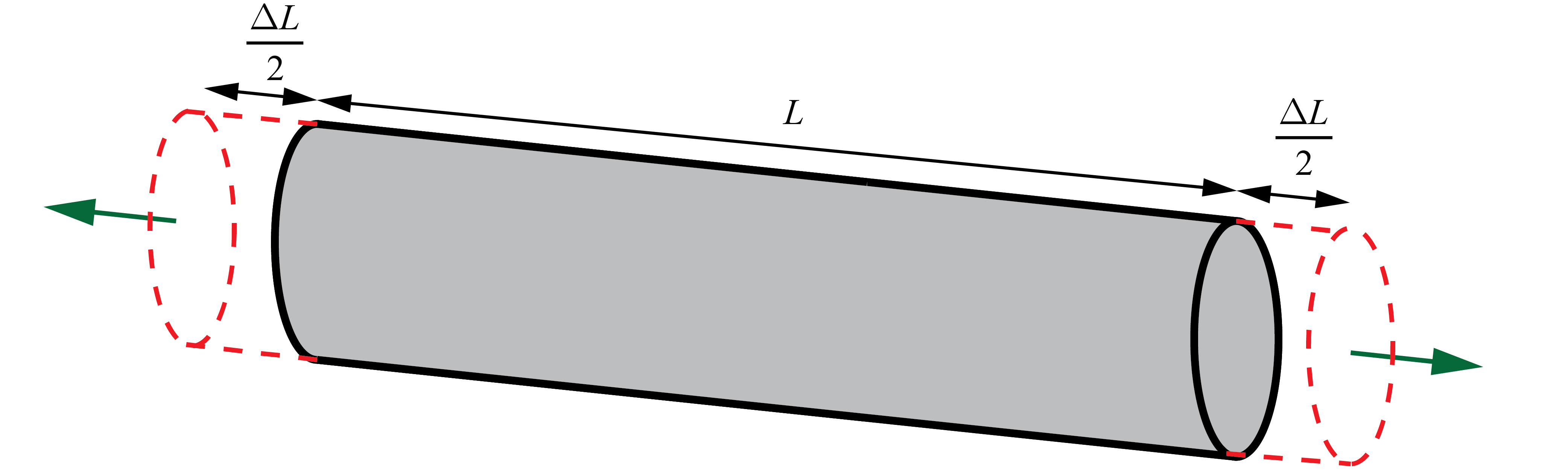
La tensión y deformación producidas no toman valores cualesquiera ya que están ligadas entre sí por la curva tensión-deformación que se obtiene en el ensayo de tracción. A partir de esta curva es posible correlacionar qué valor de tensión corresponde para cada grado de deformación, y viceversa.
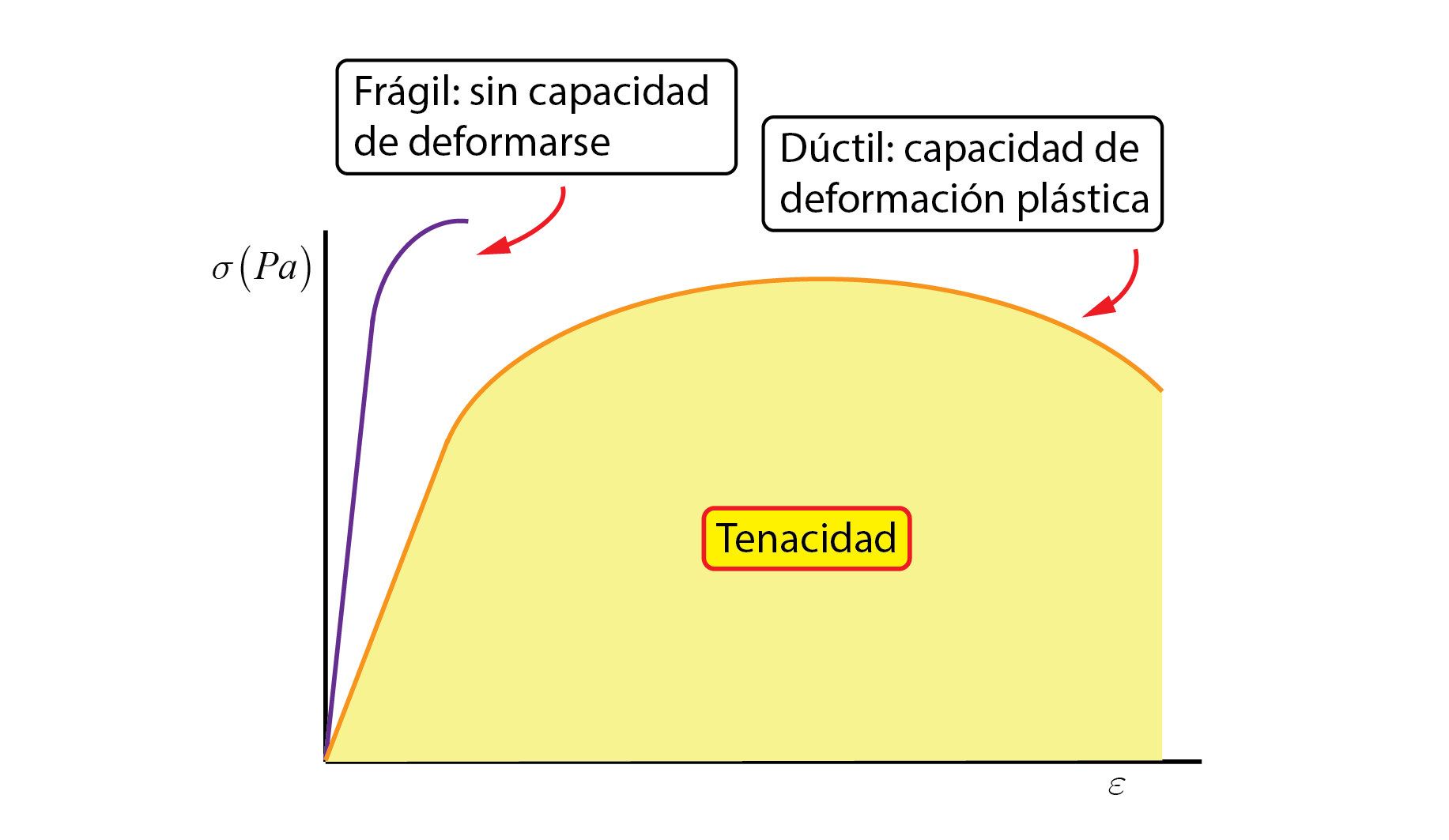
Como es lógico, cada material presenta una curva tensión-deformación distinta que describe cómo es su comportamiento: frágil o dúctil. Si necesitáis más información sobre el Ensayo de tracción, cómo se lleva a cabo y todos los datos que aporta os invito a leer el artículo que específicamente trata este tema en el siguiente enlace.
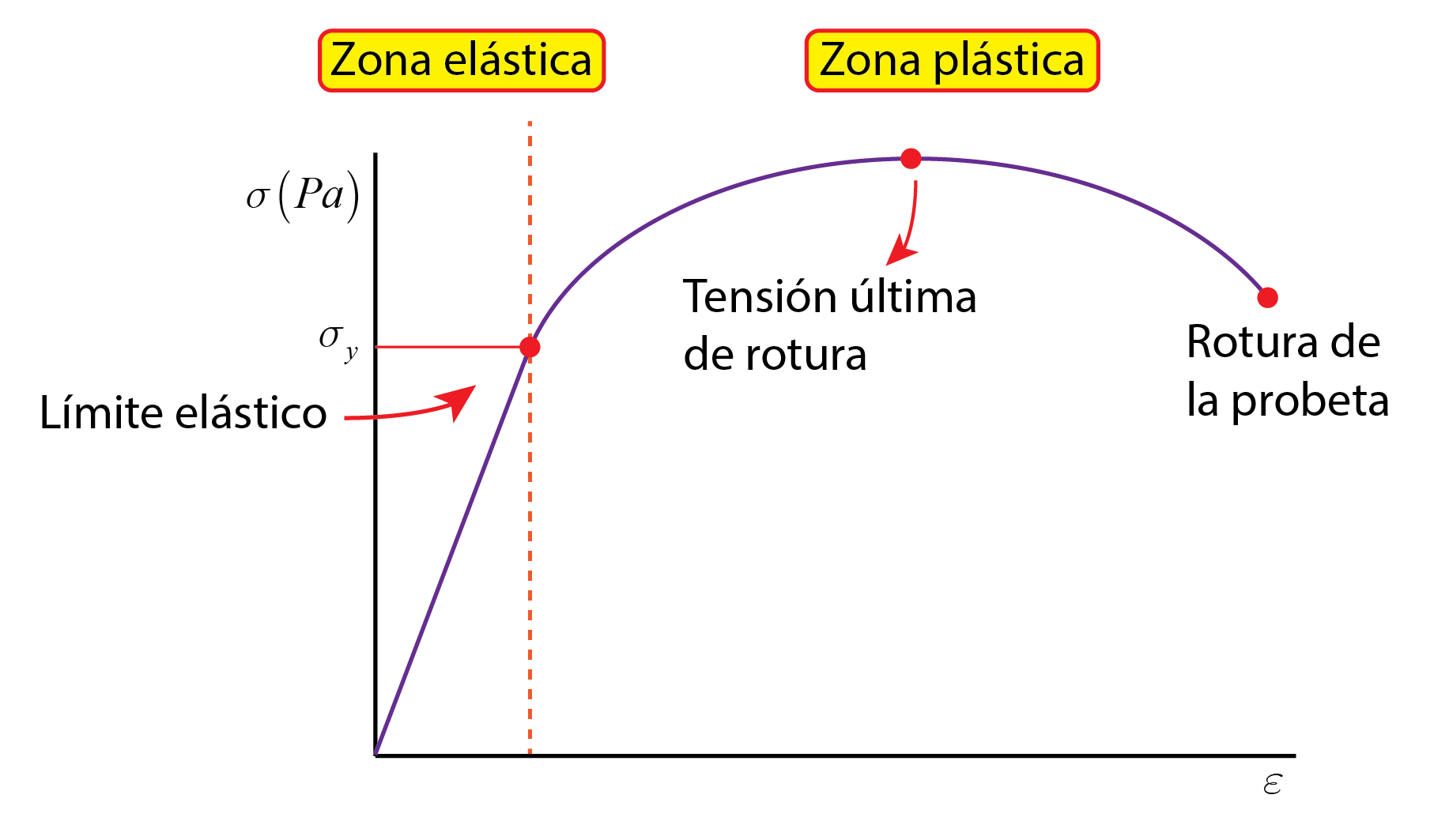
Por último, viendo que los esfuerzos de tracción y compresión son similares pero opuestos, ya que únicamente cambia el signo de la tensión generada y la deformación producida, pero los valores obtenidos para iguales cargas aplicadas son similares, podríamos preguntarnos si todos los materiales resisten igual las tracciones y las compresiones.
En el caso de materiales isótropos, como la mayoría de los metales, la resistencia a la tracción y la compresión suelen ser similares. Sin embargo, hay otros materiales como el hormigón, que son muy resistentes ante los esfuerzos de compresión, pero débiles ante la tracción. Por este motivo, se introducen armaduras de acero creando el hormigón armado.
Además, cuando una pieza esbelta (delgada y larga) está sometida a compresión, puede aparecer el Pandeo, causando una inestabilidad que genera una deformación exagerada de la barra para cargas bajas, muy inferiores a aquellas que superan el límite de resistencia. Si queréis más información sobre el pandeo y cómo evitarlo, os animo a echarle un ojo al artículo que tenemos en el siguiente enlace.
En el siguiente vídeo explicamos estos conceptos de manera más detallada…¡y con animaciones!
