Los incrementos de temperatura en las estructuras generan deformaciones y tensiones en las vigas que, de no tenerse en cuenta y controlarse, pueden conducir al colapso y el fallo del material. En este artículo explicamos cómo evaluar las deformaciones y tensiones normales en vigas isostáticas e hiperestáticas sometidas a incrementos uniformes de temperatura y gradientes térmicos. También tenemos un vídeo con otros ejemplos resueltos al final del artículo.
Si tenéis dudas sobre algún concepto previo u os estáis iniciando en el cálculo de vigas, os recomendamos ojear este artículo previo.
1. Cargas térmicas en vigas
Las estructuras, y más en concreto una viga, puede estar sometida a dos tipos de cargas térmicas:
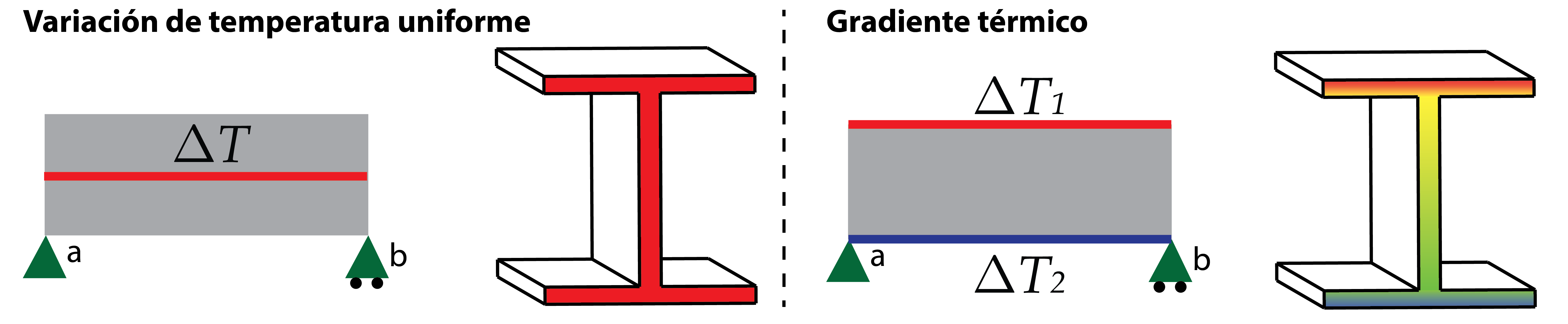
- Variación de temperatura uniforme en toda la longitud de la viga: todos los puntos del perfil están sometidos a la misma variación de temperatura. Es el caso más sencillo de análisis.
- Gradiente térmico: existe una diferencia de temperatura entre las alas del perfil, provocando una variación lineal a lo largo del perfil.
El efecto de las cargas térmicas en las vigas y estructuras es distinto dependiendo de si es isostática o hiperestática:
- Vigas isostáticas: las cargas térmicas producen deformaciones en los elementos (longitudinales y angulares) sin generar tensiones.
- Vigas hiperestáticas: debido a la restricción de desplazamientos, se generan tensiones normales (tracción o compresión). No se producen deformaciones.
A continuación, se detallan los dos tipos de cargas térmicas y sus efectos en vigas isostáticas e hiperestáticas.
2. Variación de temperatura uniforme
Este tipo de carga térmica es la más habitual, y también la más sencilla de analizar. Todos los puntos del perfil de la viga sufren la misma variación de temperatura, ΔT, ya sea positiva o negativa. Esta hipótesis de carga también asume que toda la longitud de la viga está expuesta al mismo incremento térmico.
Efecto en vigas isostáticas
Los materiales, y más concretamente, los metales se deforman con los cambios de temperatura. Se dilatan si son calentados y se contraen si se enfrían. Este es el motivo que explica que cada tramo de los raíles de las vías del tren estén separados una cierta distancia, con el objetivo de compensar la dilatación producida en los meses de verano cuando el metal alcanza altas temperaturas.
Esta variación de longitud está definida por el coeficiente de dilatación lineal, α, que representa el alargamiento que experimenta un material cuando su temperatura se eleva 1 ºC (1 K si se trabaja en el sistema internacional). El coeficiente de dilatación lineal es diferente para cada material, siendo \alpha = 1,2 \cdot {10^{ – 5}}{\;^ \circ }{C^{ – 1}} para el caso del acero (material más común en la construcción de vigas y estructuras).
Las vigas isostáticas, como una viga biapoyada o una viga empotrada, permiten que se puedan producir las variaciones de longitud por incremento térmico, produciéndose deformaciones en la viga. Esto lo podemos observar fácilmente en una viga biapoyada. Si se incrementa la temperatura, produciendo una dilatación, el apoyo móvil (b) se desplazará sin ninguna oposición. Todavía más claro queda en una viga empotrada, la cual incrementará su longitud ya que el voladizo no tiene ninguna restricción.
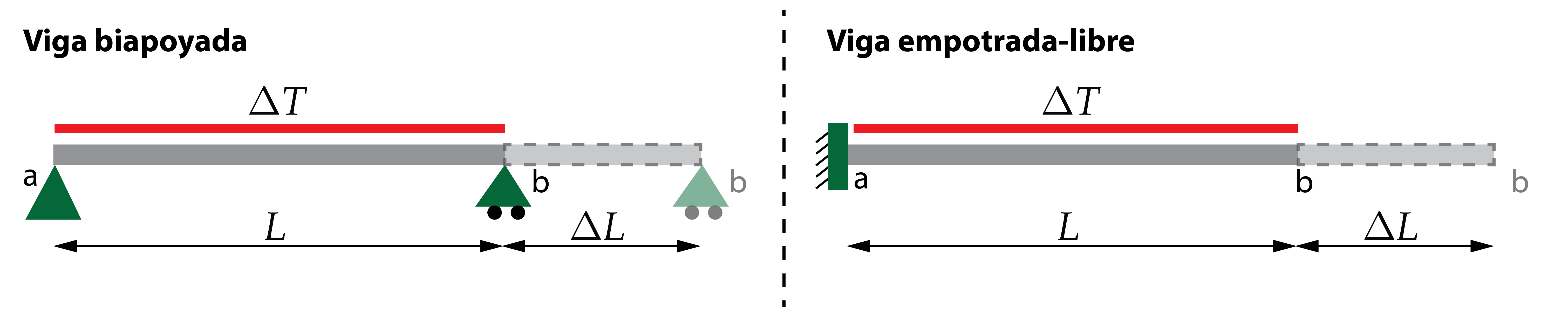
Por lo tanto, la variación de longitud en una viga, ΔL, que se encuentre sin ninguna restricción (libre) quedará definida por el coeficiente de dilatación lineal, α, la variación de temperatura, ΔT, y la longitud inicial de la viga, L.
\Delta L = \alpha \cdot \Delta T \cdot L
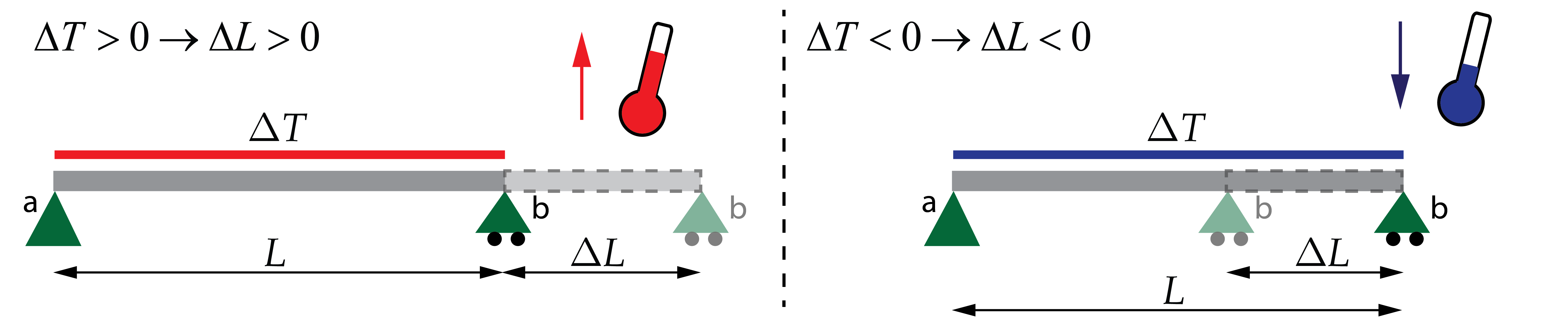
Si la variación de temperatura es positiva (incremento de temperatura) la variación de longitud también lo será, la viga se dilata. En contrario, si se trata de una variación negativa (descenso de temperatura), se producirá una reducción de longitud, es decir, la viga se contrae.
La deformación unitaria en la viga, ε, puede calcularse, a partir de su definición, como
\varepsilon = \dfrac{{\Delta L}}{L} = \alpha \cdot \Delta T
Al producirse la deformación sin ninguna restricción o limitación, no se generarán tensiones en la viga. Es decir, existirá deformación sin tensión, únicamente por efecto de dilatación o contracción térmica.
Estos mismos fundamentos son extrapolables a estructuras isostáticas, como pórticos o estructuras articuladas. Cualquier variación térmica producirá un conjunto de deformaciones en la estructura global sin generación de tensiones normales.
Efecto en vigas hiperestáticas
El caso contrario observamos en vigas hiperestáticas. Para visualizarlo, pongamos como ejemplo una viga con dos apoyos fijos (hiperestática de grado 1). Al tratarse de dos apoyos que no permiten el desplazamiento (el único que permite el movimiento es el apoyo deslizante), la deformación de la viga estará impedida cuando esta sea sometida a una variación térmica.
Como resultado, aparecerá un esfuerzo axial en la viga que es respuesta al intento de dilatación o contracción.
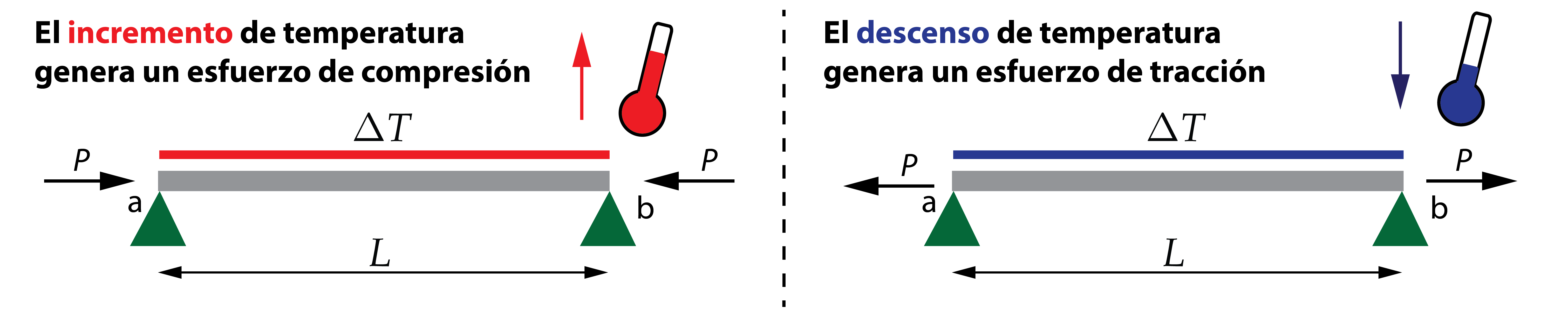
- Si la variación de temperatura es positiva, la viga intentará dilatarse (aumentar su longitud), pero no logrará conseguirlo. Como resultado, aparecerá un esfuerzo de compresión.
- Si la variación de temperatura es negativa, la viga intentará contraerse (acortar su longitud), pero los apoyos le impedirán esta deformación, tirando de ella. Como resultado, aparecerá un esfuerzo de tracción.
Ya hemos deducido previamente la deformación unitaria, ε, que sufriría la viga en caso de ser isostática. La tensión normal generada por el esfuerzo axial puede calcularse a partir de esta deformación, teniendo en cuenta la Ley de Hooke y el módulo elástico, E, del material.
\sigma = – E \cdot \varepsilon = E \cdot \alpha \cdot \Delta T
Así, para una deformación positiva, lo que corresponde para un aumento de temperatura, la tensión normal es negativa (compresión). En caso de un descenso térmico, cuya deformación es negativa, la tensión normal es positiva (tracción).
A partir de la tensión normal y el área del perfil podemos deducir la carga, P, que produciría la misma tensión normal como
P = – E \cdot A \cdot \alpha \cdot \Delta T
También resulta interesante deducir qué variación de temperatura produce el fallo del material por alcanzar la tensión límite (normalmente establecida en el límite elástico).
\sigma < {\sigma _{\lim }}\quad \to \quad \Delta T < \dfrac{{{\sigma _{\lim }}}}{{E \cdot \alpha }}
En este análisis se está obviando el fenómeno del pandeo que podría ocurrir en el caso de que aparezcan tensiones de compresión.
3. Gradiente térmico
Esta hipótesis de carga define variaciones de temperaturas distintas en las fibras extremas del perfil, generando un gradiente térmico lineal entre las distintas fibras de la sección. La parte superior del perfil esta sometida a una variación de temperatura ΔT1, mientras que la parte inferior se aplica una variación térmica ΔT2.
Bajo estas condiciones, el gradiente térmico producido, Ty, entendido como la variación de temperatura dividida entre el canto de la sección, d, se calcula como
{T_y} = \dfrac{{\Delta {T_1} – \Delta {T_2}}}{d}
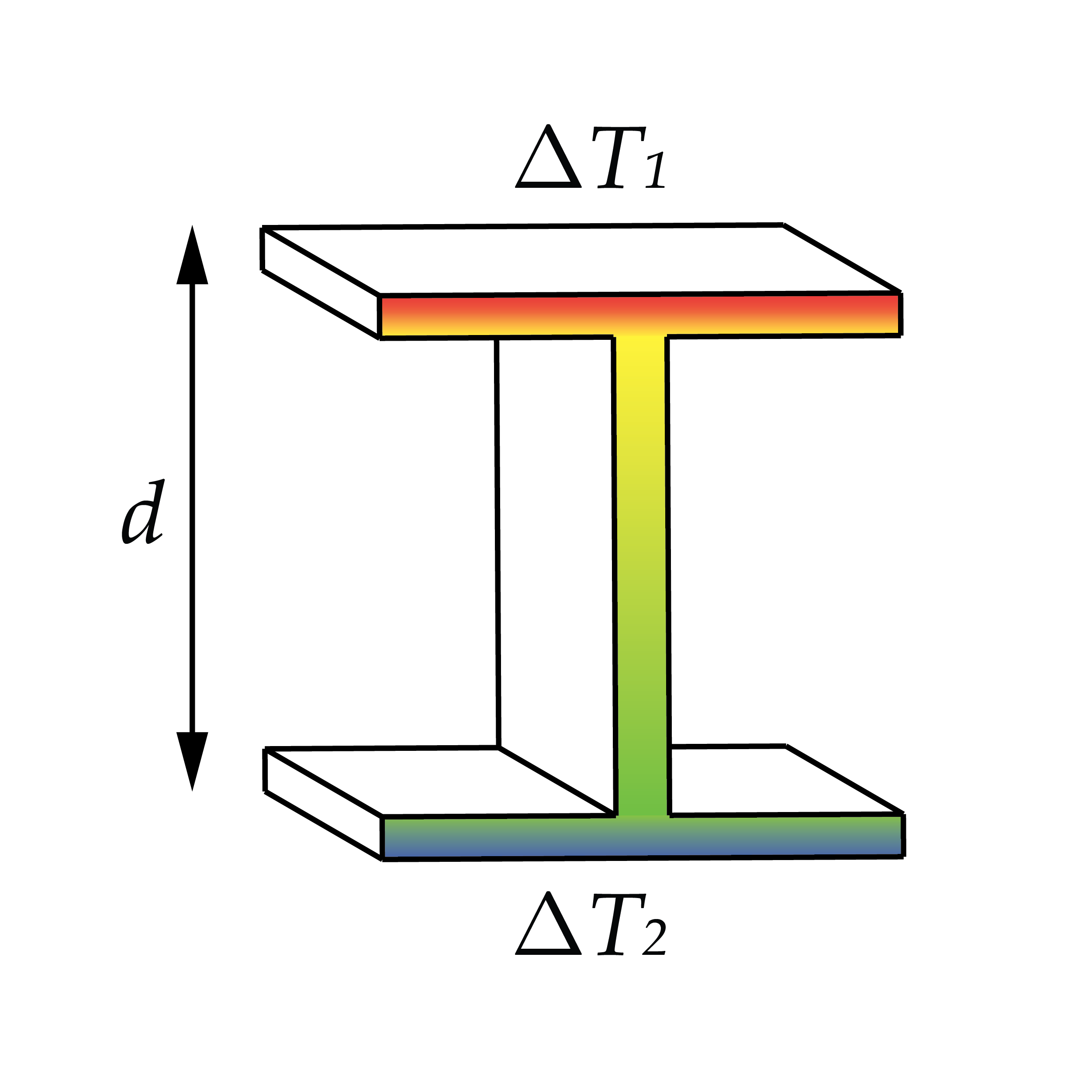
De esta fórmula se deduce lo siguiente:
- Si la diferencia entre las variaciones de temperatura en ambos extremos del perfil, ΔT1-ΔT2, aumenta, el gradiente térmico se incrementa.
- Si el canto de la sección, d, se reduce, el gradiente térmico aumenta.
Efecto en vigas isostáticas
Al igual que ocurre para el caso de variaciones de temperatura uniformes, un gradiente térmico aplicado en una viga isostática produce deformaciones en la viga, sin que se generen tensiones normales de tracción o compresión. Sin embargo, la naturaleza de esta deformación es algo distinta.
Para entenderlo, vamos a fijarnos en una rebanada diferencial de la viga, ds, en cuyas zonas superior e inferior se aplican unas variaciones de temperatura ΔT1 y ΔT2 respectivamente. Asumiremos que ΔT1 > ΔT2 > 0.
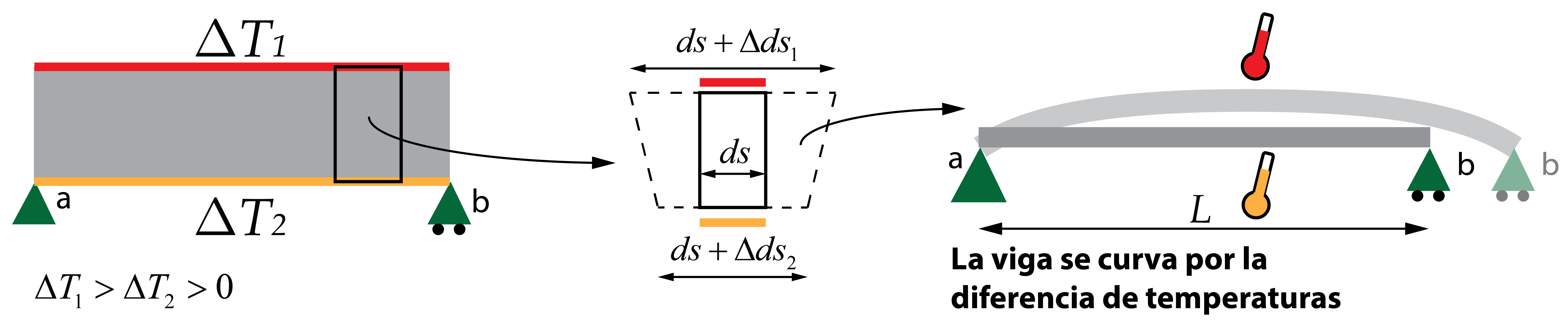
Ambas zonas, superior e inferior, se dilatarán al estar sometidas a un incremento térmico, siendo la dilatación de la zona superior mayor que el incremento de longitud en la zona inferior. Es posible deducir la deformación unitaria en cada zona, dividiendo el incremento de longitud Δds entre la longitud inicial de la rebanada, ds.
\begin{array}{l} {\varepsilon _1} = \dfrac{{\Delta d{s_1}}}{{ds}} = \alpha \cdot \Delta {T_1} \\ \\ {\varepsilon _2} = \dfrac{{\Delta d{s_2}}}{{ds}} = \alpha \cdot \Delta {T_2} \\ \end{array}
La diferencia de temperatura en ambos extremos de la sección origina que la deformación producida sea distinta. Si este análisis se extrapola al resto de la viga, veremos como la longitud total de la viga es mayor en la zona superior del perfil que en la zona inferior, generando una curvatura.
La curvatura de la viga es evaluada multiplicando el gradiente térmico, Ty, por el coeficiente de dilatación lineal, α.
\phi = \alpha \cdot {T_y} = \dfrac{{\alpha \cdot \left( {\Delta {T_1} – \Delta {T_2}} \right)}}{d}
De la fórmula deducimos que, cuanto mayor sea el gradiente térmico (bien porque el canto de la viga es pequeño o porque la diferencia de temperatura entre ambas zonas, superior e inferior, es grande), mayor será la curvatura producida en la viga.
Efecto en vigas hiperestáticas
En la viga biapoyada anterior, el gradiente térmico aplicado en toda la viga genera la curvatura de la misma debido a que los apoyos fijo y deslizante permiten el giro de la sección.
En el caso de una viga biempotrada, que es hiperestática, el giro en los extremos de la viga está impedido, evitando que su curvatura sea libre. Como resultado de esta deformación impedida, se producirá un momento flector constante, M, en toda la longitud que puede calcularse como
M = \dfrac{{E \cdot I \cdot \alpha \cdot \left( {\Delta {T_1} – \Delta {T_2}} \right)}}{d}
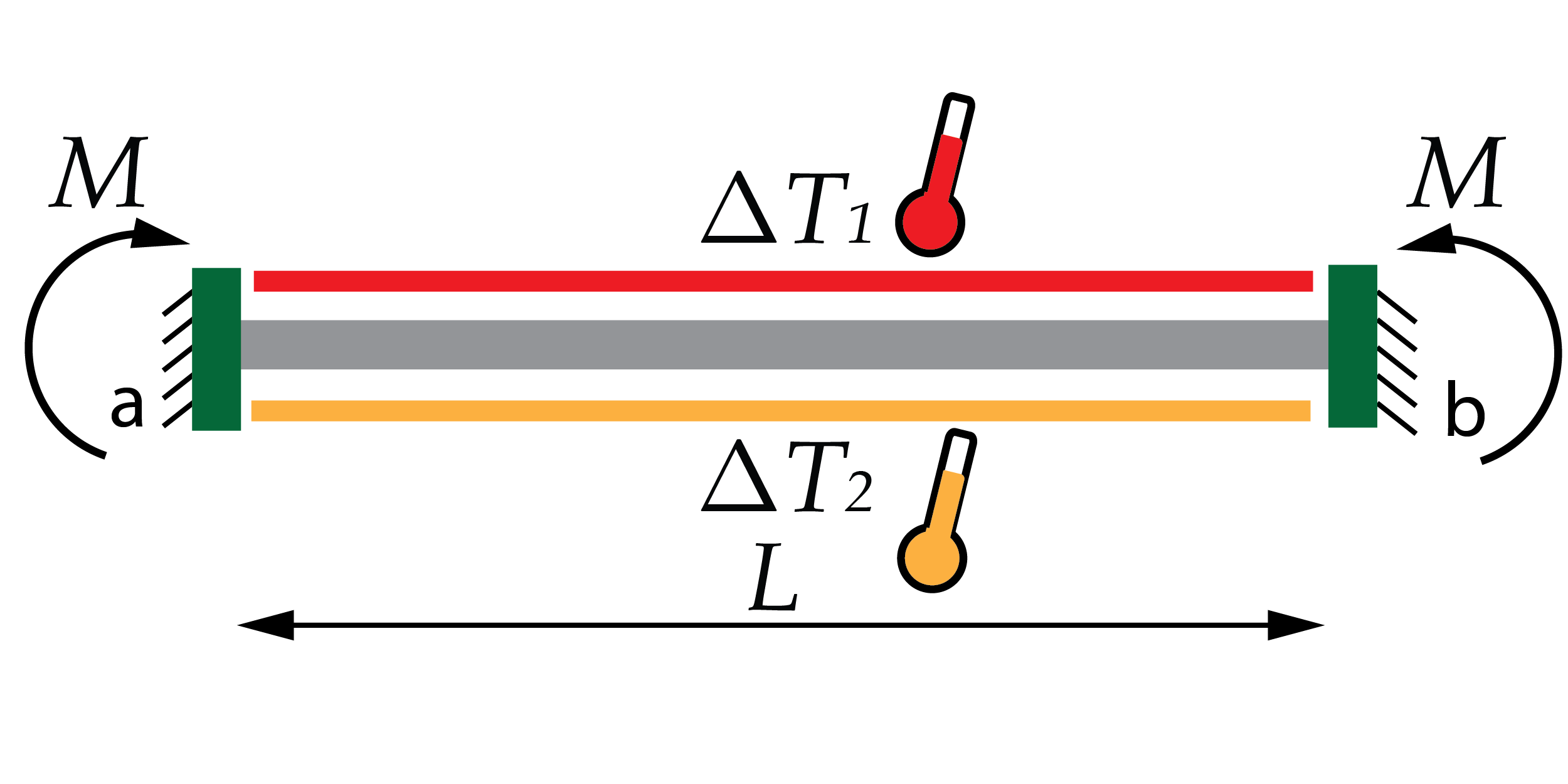
Es decir, depende del módulo elástico del material, E, el momento de inercia de la sección, I, el coeficiente de dilatación lineal, α, y el gradiente térmico, Ty.
Por último, no te pierdas el siguiente vídeo con animaciones donde también resolvemos algún ejercicio
