Las vigas con rótulas son muy comunes. Las rótulas son conexiones que permiten el giro entre los elementos, de modo que el momento flector en la sección de la rótula es nulo. El planteamiento de ejercicios sobre el cálculo de reacciones, leyes y diagramas de esfuerzos en vigas con rótulas es muy común en las carreras de ingeniería. En este artículo explicamos el procedimiento para la resolución de este tipo de vigas paso a paso. También tenemos un vídeo con otros ejemplos resueltos al final del artículo.
Si tenéis dudas sobre algún concepto previo u os estáis iniciando en el cálculo de vigas, os recomendamos ojear este artículo previo.
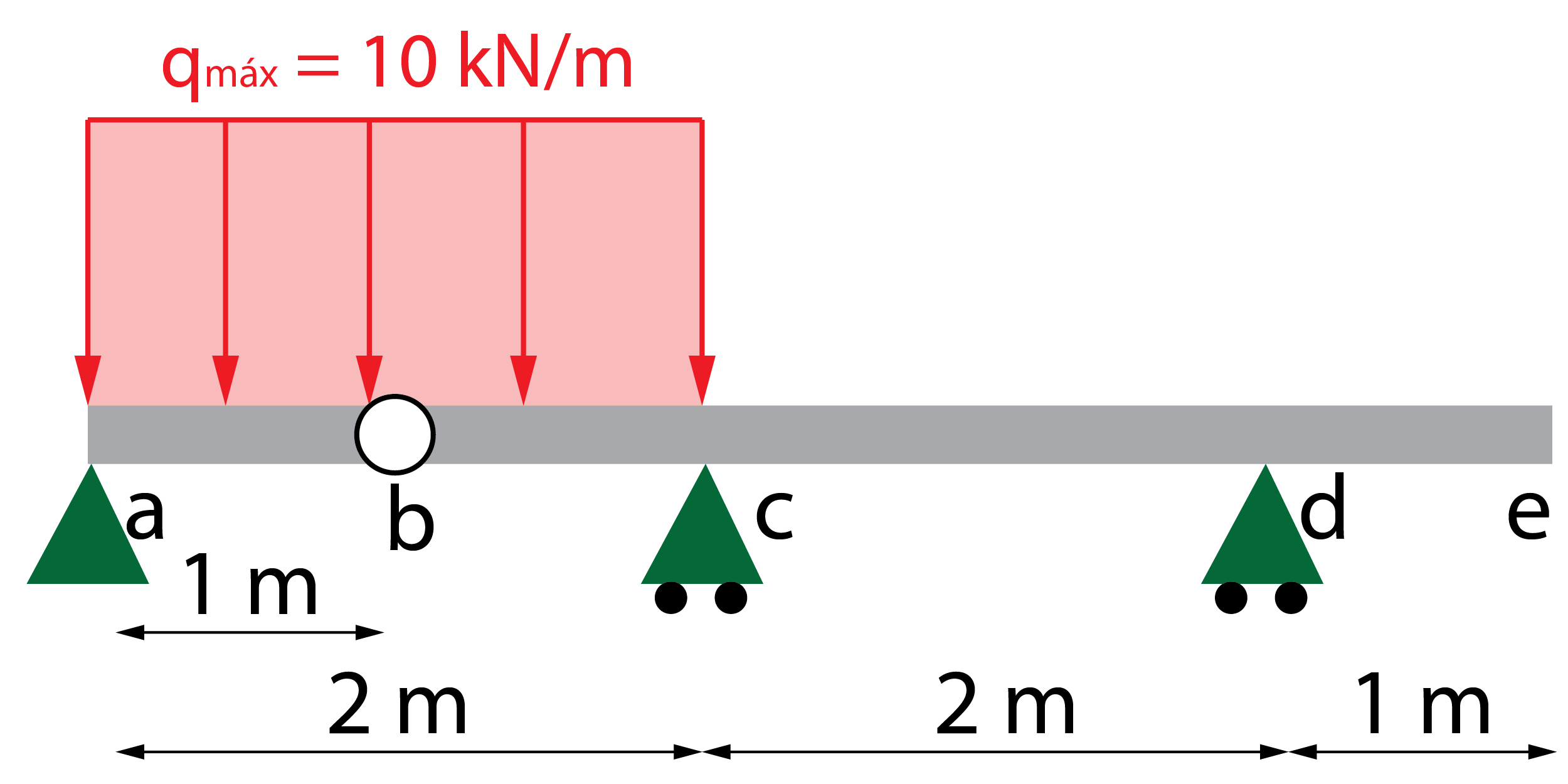
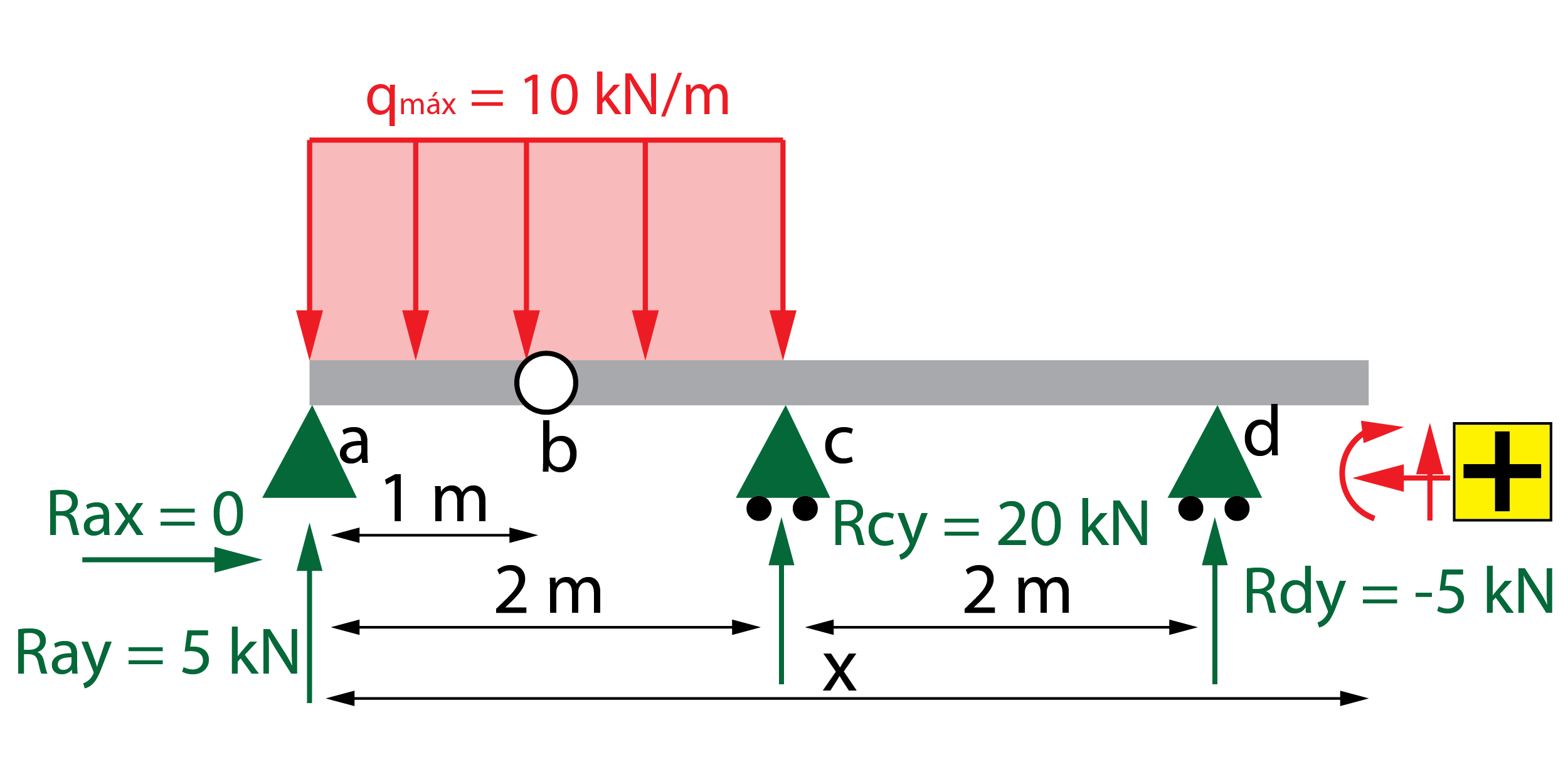
Calcular las reacciones, determinar las leyes de esfuerzos y representar los diagramas de esfuerzos para la siguiente viga que tiene una rótula en la sección b.
1. Determinación de las reacciones en vigas con rótulas
El primer paso consiste en obtener el valor de las reacciones que los apoyos definidos en la viga generan como respuesta a las cargas aplicadas.
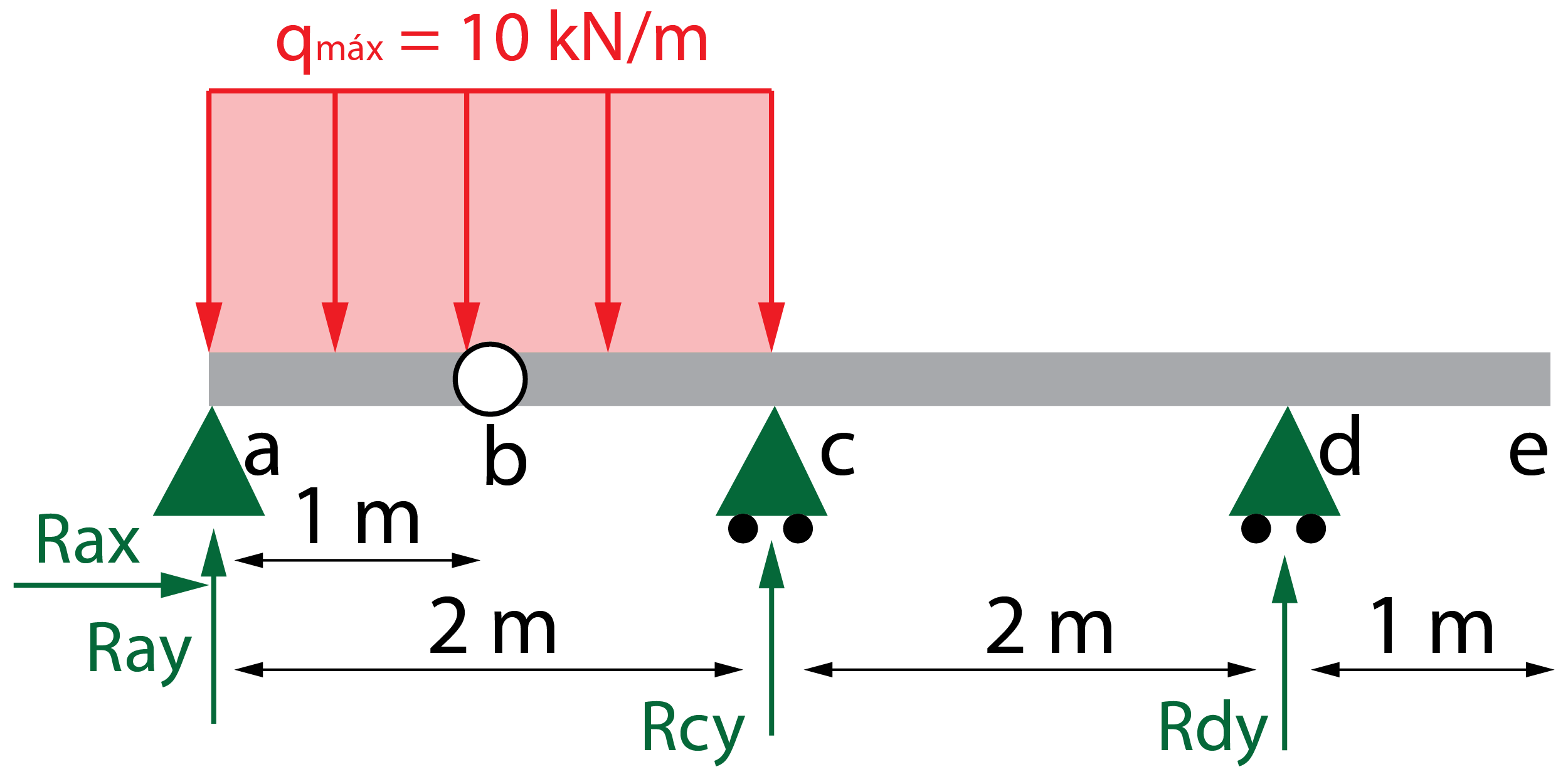
El apoyo a es un apoyo fijo, por lo que aparecen dos reacciones, Ray en dirección vertical y Rax en dirección horizontal. Los apoyos c y d son deslizaderas, generando dos reacciones verticales, Rcy y Rdy, respectivamente.
Por lo tanto, hay un total de 4 reacciones y únicamente se dispone de 3 ecuaciones estáticas: sumatorio de fuerzas horizontales y verticales y sumatorio de momentos. Puede parecer que la viga no es isostática, ya que hay una incógnita más que el número de ecuaciones disponibles.
Sin embargo, cada rótula en una viga permite obtener una ecuación adicional para la obtención de las reacciones en los apoyos. Recordemos que en la sección de la rótula (sección b) el momento flector es igual a cero. ¡Aquí está nuestra cuarta ecuación! ¡4 ecuaciones para 4 incógnitas!
Se disponen de 4 ecuaciones para obtener las 4 reacciones incógnita:
\sum {{F_x}} = 0
\sum {{F_y}} = 0
\sum {{M_a}} = 0
\left. {M\left( 1 \right)} \right|_a^c = 0
A continuación se plantean las tres ecuaciones estáticas:
- Sumatorio de fuerzas horizontales: por criterio, las fuerzas aplicadas en dirección «hacia la derecha» son positivas y las aplicadas «hacia la izquierda» son negativas. La suma de todas las fuerzas debe ser igual a cero. En este caso, únicamente la reacción Rax es horizontal, por lo que su valor es cero.
\sum {{F_x}} = 0 \to Rax = 0\;kN
- Sumatorio de fuerzas verticales: por criterio, las fuerzas aplicadas «hacia arriba» serán positivas, y las aplicadas «hacia abajo» serán negativas. La suma total de las fuerzas deber ser igual a cero. En este caso, todas las reacciones Ray, Rcy y Rdy son positiva. La carga total es negativa e igual a 2q.
\sum {{F_y}} = 0 \to Ray + Rcy + Rdy – 2 \cdot q = 0
- Sumatorio de momentos en una sección: elegiremos una sección de la viga para realizar el equilibrio de momentos. Es recomendable seleccionar aquella que más incógnitas elimine, en este caso, la sección a, ya que hay dos fuerzas aplicadas en este punto que no generan momento. En el planteamiento de esta ecuación necesitamos hacer uso de la distancia desde el punto de aplicación de las fuerzas hasta a. Para entender cómo plantear la ecuación, pensaremos en una palanca que gira respecto de la sección a, desde el punto de aplicación de cada fuerza. Si el giro es «antihorario» el signo será positivo. Si es «horario» se tomará como negativo. En este caso, las reacciones Rcy y Rdy generan un momento positivo, multiplicadas por las distancias 2 m y 4 m, respectivamente. La carga distribuida genera un momento negativo, igual a su área (2q) multiplicada por la distancia desde su centro de gravedad a la sección a (1 m).
\sum M = 0 \to 2Rcy + 4Rdy – 2 \cdot q \cdot 1 = 0
Además, necesitamos plantear la ley de momentos correspondiente al tramo a-c de la viga, ya que la rótula se encuentra en el punto medio de este tramo (en la sección 2 de este artículo se muestran cada uno de los tramos de la viga para la obtención de las leyes de esfuerzo).
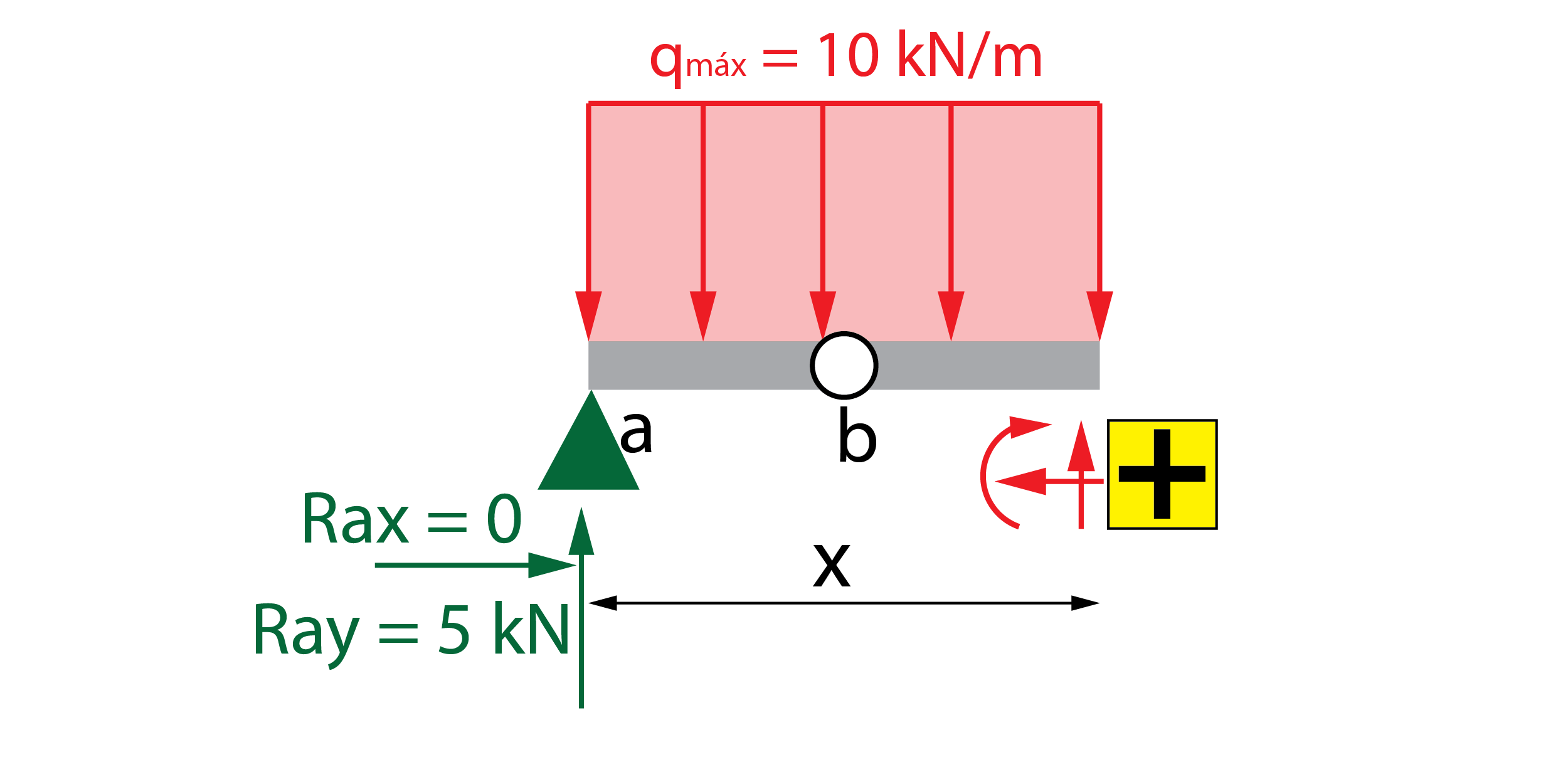
En definitiva, si analizamos la viga desde el extremo izquierdo, el momento flector en la sección b es generado por la reacción Ray, multiplicado por la distancia hasta b (1 m). Esta reacción genera un momento positivo. La carga distribuida genera un momento negativo. Igualando a cero se despeja el valor de la reacción Ray.

A partir del valor conocido de Ray = 5 kN, es posible obtener Rcy y Rdy resolviendo el sistema de dos ecuaciones con dos incógnitas formado por la ecuación de la suma de fuerzas verticales y la ecuación de suma de momentos.
\left. \begin{array}{l} \sum {{F_y}} = 0 \to 5 + Rcy + Rdy – 2 \cdot 10 = 0 \\ \sum M = 0 \to 2Rcy + 4Rdy – 2 \cdot 10 \cdot 1 = 0 \\ \end{array} \right\}
Se despeja Rcy = 20 kN y Rdy = -5 kN. Fijémonos en que el signo de Rdy es negativo, por lo que el sentido de la reacción es contrario al dibujado inicialmente. Esto puede tener sentido, ya que la viga tienen a levantarse de ese apoyo, así que la reacción intenta atraerlo hacia abajo.
2. Obtención de las leyes de esfuerzo axil, cortante y momento flector en todos los tramos de la viga
Una vez que los valores de las reacciones en los apoyos de la viga son conocidas, es posible obtener las leyes de esfuerzo en cada tramo de la viga.
Una ley de esfuerzo es una función que representa el esfuerzo axil, cortante o momento flector en todas las secciones de la viga, desde un extremo a otro en función de la posición. Para ello, definiremos distancia x como la longitud desde el extremo izquierdo de la viga hasta la sección de evaluación.
El procedimiento consiste en partir la viga en tramos, separados por cambios de carga o apoyos. Es decir, recorriendo la viga de derecha a izquierda, se definirá un tramo cuando aparezca una nueva carga o un apoyo.
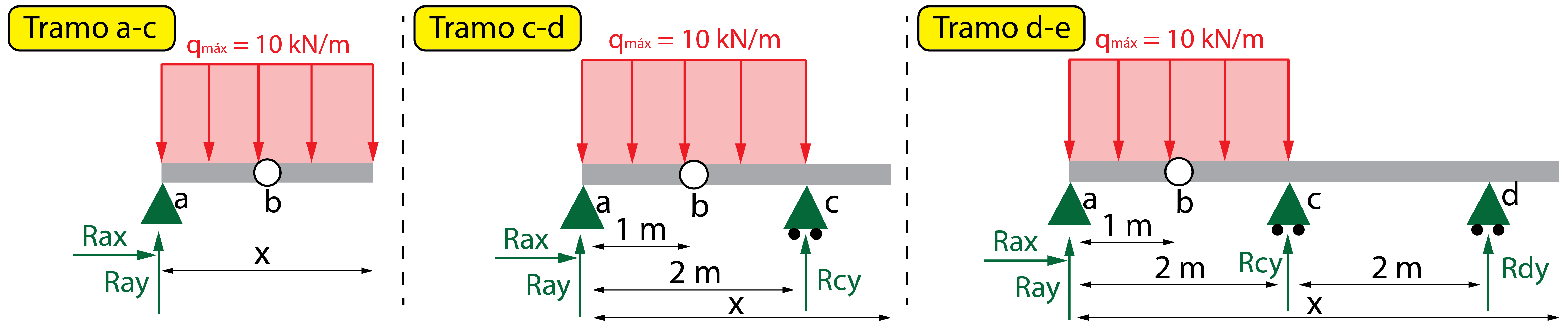
Siguiendo este criterio, esta viga se divide en tres tramos: el tramo a-c, el tramo c-d y el tramo d-e, coincidiendo con la posición de los apoyos.
Recordatorio
Antes de analizar cada tramo y obtener las leyes de esfuerzo, es necesario definir un criterio de signos. Aunque esto es algo que ya deberíamos conocer antes de analizar este tipo de vigas, repetimos aquí este recordatorio:
- Esfuerzo axil, N: se toma como criterio positivo el esfuerzo de tracción, es decir, aquellas cargas que tienen a incrementar la longitud de la barra. Por lo tanto, la compresión es negativa. A nivel del procedimiento de análisis se traduce en definir como criterio positivo todas aquellas fuerzas en dirección paralela al eje de la viga que, situadas a la izquierda de la sección x, están dirigidas hacia la izquierda.

- Esfuerzo cortante, V: aquellas fuerzas situadas a la izquierda de la sección x con dirección perpendicular al eje de la viga y hacia arriba generarán un cortante positivo.
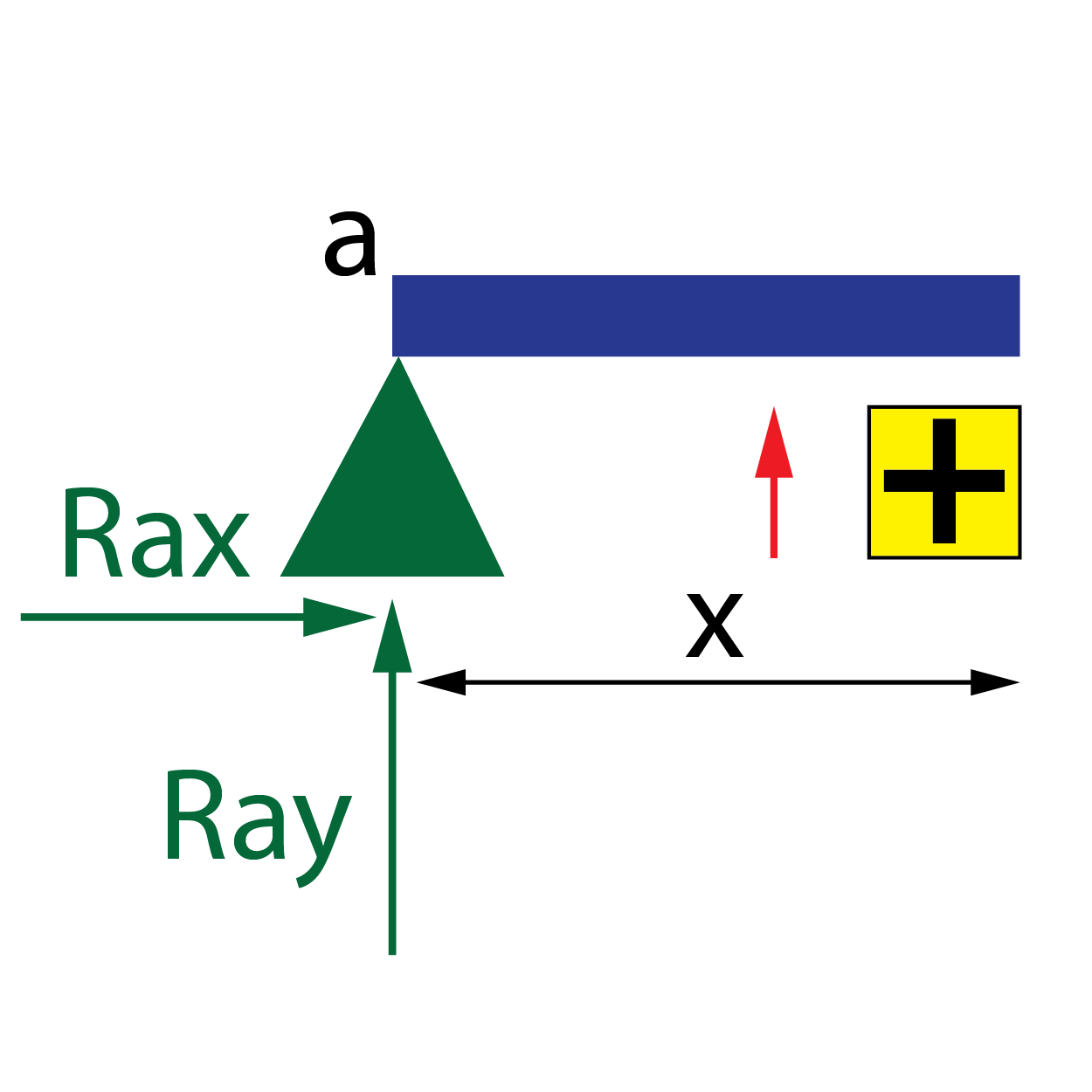
- Momento flector, M: se tomará como criterio de momento positivo, el sentido horario producido por las cargas situadas a la izquierda de la sección x.
A partir de estos criterios establecidos, podemos obtener las leyes de esfuerzos en cada uno de los tramos.
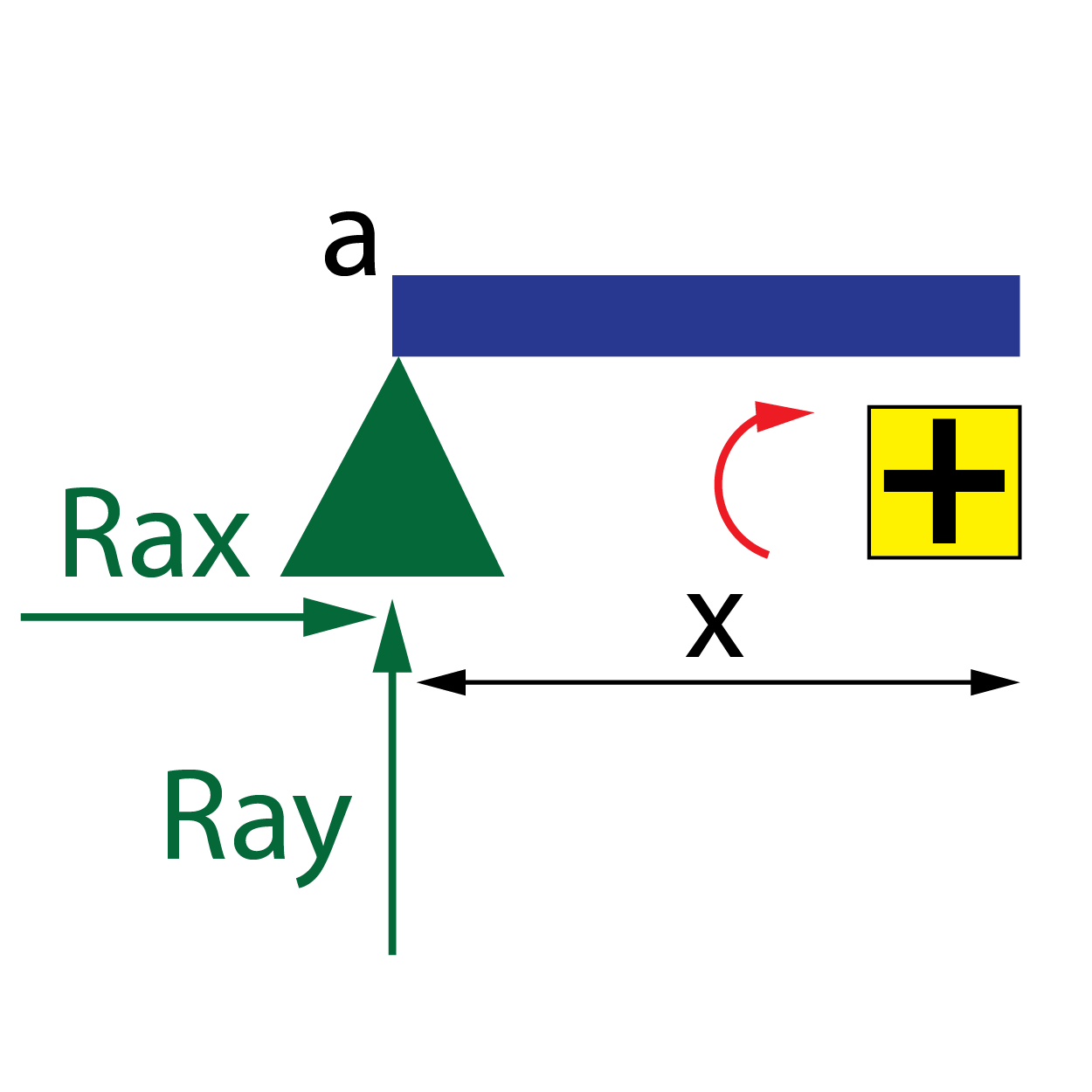
Tramo a-c
El esfuerzo axil es nulo, ya que no hay fuerzas en dirección paralela al eje de la viga.
\left. {N\left( x \right)} \right|_a^c = Rax = 0
El cortante es generado en la sección x por la reacción Ray (positivo) y por la carga distribuida (negativo). La expresión de la ley de cortante podemos expresarla como
\left. {V\left( x \right)} \right|_a^c = Ray – q \cdot x = 5 – 10x\;kN
La ley de momento flector en este tramo ha sido ya utilizada anteriormente para el planteamiento de la ecuación de la rótula. La reacción Ray, multiplicada por la distancia x, genera un momento positivo en la sección x. La carga distribuida q, cuya longitud es x, aporta un momento negativo. El centro de gravedad se encuentra a una distancia x/2. Por lo tanto, la ley queda planteada como
\left. {M\left( x \right)} \right|_a^c = Ray \cdot x – q \cdot x \cdot \dfrac{x}{2} = 5x – 5{x^2}\;kNm
Tramo c-d

El esfuerzo axil es nulo, ya que no hay fuerzas en dirección paralela al eje de la viga.
\left. {N\left( x \right)} \right|_c^d = Rax = 0
El cortante es generado en la sección x por la reacción Ray (positivo), por la carga distribuida (negativo) y por la reacción Rcy (positivo). Fijémonos en que en este tramo, toda la carga distribuida ha sido aplicada (2q), por lo que no depende de x. La ley de cortante podemos expresarla como
\begin{array}{l} \left. {V\left( x \right)} \right|_c^d = Ray – 2 \cdot q + Rcy = \\ \\ = 5 – 2 \cdot 10 + 20 = 5\;kN \\ \end{array}
El cortante es constante en este tramo, ya que no hay cargas distribuidas que dependan de la posición x.
Finalmente, obtenemos la expresión para el momento flector generado por la reacción Ray, multiplicada por x (positivo), toda la carga distribuida 2q (negativo), multiplicada por la distancia desde su centro de gravedad a la sección (x-1), y la reacción Rcy (positivo), multiplicada por la distancia (x-2)
\begin{array}{l} \left. {M\left( x \right)} \right|_c^d = Ray \cdot x – 2 \cdot q \cdot \left( {x – 1} \right) + Rcy \cdot \left( {x – 2} \right) \\ \\ = 5x – 2 \cdot 10 \cdot \left( {x – 1} \right) + 20 \cdot \left( {x – 2} \right) = 5x – 20\;kNm \\ \end{array}
Tramo d-e
El esfuerzo axil es nulo, ya que no hay fuerzas en dirección paralela al eje de la viga.
\left. {N\left( x \right)} \right|_d^e = Rax = 0
A la ley de cortantes del tramo anterior hay que sumar la reacción Rdy. Esta reacción está dibujada hacia arriba, pero su valor es negativo, por lo que genera un cortante negativo.
\begin{array}{l} \left. {V\left( x \right)} \right|_d^e = Ray – 2 \cdot q + Rcy + Rdy \\ \\ = 5 – 2 \cdot 10 + 20 – 5 = 0\;kN \\\end{array}
El cortante es nulo en este tramo ya que es un voladizo sin cargas aplicadas.
Finalmente, obtenemos la expresión para el momento flector sumando a la ley del tramo anterior el momento generado por la reacción Rdy, multiplicada por la distancia (x-4).
\begin{array}{l} \left. {M\left( x \right)} \right|_c^d = Ray \cdot x – 2 \cdot q \cdot \left( {x – 1} \right) + Rcy \cdot \left( {x – 2} \right) + Rdy \cdot \left( {x – 4} \right) \\ \\ = 5x – 2 \cdot 10 \cdot \left( {x – 1} \right) + 20 \cdot \left( {x – 2} \right) – 5 \cdot \left( {x – 4} \right) = 0\;kNm \\ \end{array}
Al igual que ocurre para el cortante, el momento flector en este tramo es nulo.
3. Representación de los diagramas de esfuerzo
El último paso para acabar un ejercicio de este tipo es representar los diagramas para los tres esfuerzos. Este paso es muy sencillo, ya que únicamente consiste en graficar las funciones que hemos obtenido en el apartado anterior para cada esfuerzo en función de la posición x de la viga.
Como única consideración importante, hay que destacar que, por cuestiones de criterio, la ley de momentos se representa invertida. Esto es, el eje de ordenadas (eje y) tiene sentido contrario, por lo que los valores positivos se representan debajo del eje, y los negativos por encima.

- Se observa como el esfuerzo axil es nulo en toda la viga, al no existir cargas aplicadas en dirección paralela al eje longitudinal de la viga.
- El esfuerzo cortante sigue una distribución lineal en el tramo a-c, siendo constante en d-c y nulo en d-e al no existir cargas en el voladizo.
- El diagrama de momento flector sigue una función parabólica en el tramo a-c debido a la aplicación de la carga distribuida uniforme (recordad que no todas las cargas distribuidas crean este tipo de diagrama, las cargas triangulares generan una distribución polinómica de grado 3). Fijémonos como justo en la sección b de la rótula el momento es cero, tal cual se ha planteado inicialmente. La distribución es lineal en el tramo c-d y nulo en d-e, al no existir cargas aplicadas en el voladizo.
- Además, existe una relación directa entre la ley de cortante y de momento flector. La ley de cortante es la derivada del momento flector.
Existe un tipo de viga con rótulas muy particular y famosa, utilizada en construcciones como puentes de ferrocarril, llamada viga Gerber.Si quieres aprender un poco más cómo analizar vigas de este tipo y resolver otros ejemplos, aquí tienes este vídeo!!!
